0669

Robust Coil Combination for bSSFP Elliptical Signal Model
Nicholas McKibben1,2, Grayson Tarbox3, Edward V. DiBella1,2, and Neal K. Bangerter4
1Biomedical Engineering, University of Utah, Salt Lake City, UT, United States, 2Radiology and Imaging Sciences, University of Utah, Salt Lake City, UT, United States, 3Electrical and Computer Engineering, Brigham Young University, Provo, UT, United States, 4Bioengineering, Imperial College London, London, United Kingdom

Synopsis

Elliptical parametric models of the bSSFP signal equation are used to derive band-free images given multiple phase-cycled images. For large multicoil datasets, we desire coil combination before debanding to significantly reduce computational burden. Conventional coil combination methods fail as nonlinear mappings lead to distortions of the elliptical representation. We propose phase-substitutions that can be applied with any coil combination method including sum-of-squares and which allow coil combination before computationally expensive debanding operations.

Introduction

BSSFP is a fast, SNR-efficient sequence that suffers from dark banding artifacts due to its off-resonance dependence1. These artifacts can be mitigated, usually by acquiring multiple linearly phase-cycled images2,3,4. The elliptical signal model is a parametric representation of the bSSFP signal equation where phase-cycles lie on ellipses in the complex-plane5,3. The linearized geometric solution (lGS) is an analytic solution for the single debanded image given four phase-cycles3.

The lGS is defined for single-coil datasets, requiring coil-by-coil solution before coil combination6. Coil combination prior to lGS is desired for reduced computational burden, but due to nonlinearities of the lGS and some coil combination methods this yields large artifacts7. Artifacts arise due to distortion of the elliptical relationships between pixels of phase-cycled images (Figure 1). This is especially problematic when coil combination uses phase-alignment to produce smoothly varying coil sensitivities8,9,10.

Preserving phase information during coil combination is much studied11-17. Some techniques are unsuited for use with the lGS due to additional acquisitions13,17 or failure in low-SNR areas, e.g. around banding and for larger FOVs at high field strengths13,16,18. They also do not guarantee reference phase that preserves elliptical relationships.

We present a phase-substitution scheme for use with coil combination that successfully mitigates artifacts and maintains the elliptical relationships required by the lGS. We do not consider methods requiring prior knowledge of coil sensitivities and consider only maximum coil compression.

Theory

The magnitude of the coil-combined $$$i$$$th phase-cycle is generally a good estimate of the magnitude of the equivalent single-coil phase-cycle: $$$| I_{i, \text{coil-combined}} | \approx | I_{i, \text{single-coil}} |,$$$ e.g. sum-of-squares (SOS), maximum-SNR coil combination, adaptive coil combination or stochastic matched filter (SMF), geometric coil combine (GCC)8,10,19,20. The phase of the combined images is problematic. If we estimate the phase of the combined phase-cycles, then many coil combination methods become viable as preprocessing steps to the lGS.

Phase is taken from a composite ellipse for each pixel. The composite ellipse is constructed by finding the inverse transformation $$$T_{j}(x,y)$$$ required to co-register the $$$j$$$th coil ellipse at $$$(x,y)$$$ and treating these as "sensitivities" relating intra-phase-cycle coil images: $$
\angle \begin{bmatrix} I_{0, \text{composite}}(x,y) \\ I_{1, \text{composite}}(x,y) \\ I_{2, \text{composite}}(x,y) \\ I_{3, \text{composite}}(x,y) \end{bmatrix} := \angle \left( \frac{ \boldsymbol{T}^H(x,y) \boldsymbol{\sigma}^{-2} }{ \boldsymbol{T}^H(x,y) \boldsymbol{\sigma}^{-2} \boldsymbol{T}(x,y) } \begin{bmatrix} \boldsymbol{I}_0(x,y) \\ \boldsymbol{I}_1(x,y) \\ \boldsymbol{I}_2(x,y) \\ \boldsymbol{I}_3(x,y) \end{bmatrix} \right). $$

This max-SNR reconstruction uses the inverse transformations as sensitivity weightings19. Coil ellipses in the complex plane are formed through the transformations, $$$T_j(x,y)$$$. $$$T_j(x,y)$$$ is a complex number which rotates and scales phase-cycle points to match a reference ellipse. The reference should be the same shape and location in the complex plane as the unknown true ellipse. We do not know the true ellipse, but a simple choice is the pixel's largest coil-ellipse, i.e., choose the coil-ellipse with greatest average magnitude. We call this method "full phase-substitution." For increased computational savings, choose the coil-ellipse with maximum magnitude. Only a max operation is required across coils yielding significant computational savings compared to the full composite ellipse or coil-by-coil lGS. We call this simple approximation "simple phase-substitution."

Methods

We selected three coil combination algorithms for all experiments: SOS, GCC, and SMF. SOS is especially interesting as it clearly does not preserve phase information and cannot be applied alongside the lGS without phase estimation. Computer simulations, phantom, and in vivo experiments were performed for each method using the proposed phase-substitutions and coil-by-coil lGS.

A 256x256 slice through a uniform cylindrical digital reference object (T1/T2=1.5s/0.8s) with simple coil sensitivities were simulated for 4 phase-cycles with sequence parameters: TR=3ms, FA=30°. Off-resonance was simulated as a linear gradient along the x-axis between $$$\pm$$$1/TR Hz for obvious banding.

Axial slices of a cylindrical doped-water phantom were acquired on a Siemens TIM Trio 3T scanner using an 8-channel coil. A modified TrueFISP sequence was used to acquire 4 phase-cycled images; TE/TR: 3ms/6ms, BW: 558 Hz/Px, matrix size: 256x256, FOV: 150x150mm2, averages: 8, FA: 70°. 200 dummy-pulses were used to ensure steady-state.

Axial slices of a 24 year old female participant's brain were acquired using the same setup with parameters: TR/TE: 10ms/5ms, BW: 543 Hz/Px, matrix size: 512x512, FOV: 250x250mm2, averages: 16, FA: 15°. The participant gave written informed consent prior to participation according to IRB guidelines.

Results

Figures 2 and 3 show the results of the computer simulations. In all cases the proposed phase substitutions produce lowest NRMSE. Interestingly, SOS with the proposed phase substitutions produce the lowest NRMSE.

Figures 4 and 5 show reconstructions and residuals for the phantom and in vivo experiments, respectively. Naively coil combining followed by lGS results in serious artifacts and phase discontinuities while the proposed phase-substitutions always produce lowest NRMSE.

Discussion and Conclusion

The proposed method works across all implemented coil combination methods and yields artifact-free reconstructions when used prior to the lGS. Alongside the SMF, phase-singularities were completely avoided with little additional cost. The SOS using phase-substitutions appears to have desirable noise properties (Figure 3, row 1) and the reconstructions consistently show lowest error. This suggests that the proposed phase-substitutions are accurate, as SOS is the optimal magnitude estimate. SOS and the proposed phase-substitutions are also significantly easier to compute compared to SMF and GCC.

Acknowledgements

No acknowledgement found.

References

  1. Carr, H. Y. "Steady-state free precession in nuclear magnetic resonance." Physical Review 112.5 (1958): 1693.
  2. Bangerter, Neal K., et al. "Analysis of multiple‐acquisition SSFP." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 51.5 (2004): 1038-1047.
  3. Xiang, Qing‐San, and Michael N. Hoff. "Banding artifact removal for bSSFP imaging with an elliptical signal model." Magnetic resonance in medicine 71.3 (2014): 927-933.
  4. Wang, Yi, et al. "Phase‐cycled simultaneous multislice balanced SSFP imaging with CAIPIRINHA for efficient banding reduction." Magnetic resonance in medicine 76.6 (2016): 1764-1774.
  5. Dharmakumar, Rohan, and Graham A. Wright. "Understanding steady‐state free precession: A geometric perspective." Concepts in Magnetic Resonance Part A: An Educational Journal 26.1 (2005): 1-10.
  6. G. Tarbox, J. Valentine, M. Taylor, and N. K. Bangerter, “bSSFP elliptical signal model with GRAPPA parallel imaging,” Proceedings of the 25th Annual Meeting of the ISMRM; Honolulu, Hawaii, USA, 2017. 28
  7. N. McKibben, G. Tarbox, M. A. Mendoza, and N. K. Bangerter, “Analysis of coil combination for bSSFP elliptical signal model,” Proceedings of the 27th Annual Meeting of the ISMRM; Montreal, Canada, vol. 7213, 2019. ii, 1, 4, 28
  8. Zhang, Tao, et al. "Coil compression for accelerated imaging with Cartesian sampling." Magnetic resonance in medicine 69.2 (2013): 571-582.
  9. Uecker, Martin, and Michael Lustig. "Estimating absolute‐phase maps using ESPIRiT and virtual conjugate coils." Magnetic resonance in medicine 77.3 (2017): 1201-1207.
  10. Inati, S. J., M. S. Hansen, and P. Kellman. "A solution to the phase problem in adaptive coil combination." ISMRM proceeding; 20–26 april; Salt Lake City, Utah, USA 2672 (2013).
  11. Haacke, E. Mark, et al. "Susceptibility weighted imaging (SWI)." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 52.3 (2004): 612-618.
  12. Ishihara, Yasutoshi, et al. "A precise and fast temperature mapping using water proton chemical shift." Magnetic resonance in medicine 34.6 (1995): 814-823.
  13. Robinson, Simon Daniel, et al. "An illustrated comparison of processing methods for MR phase imaging and QSM: combining array coil signals and phase unwrapping." NMR in Biomedicine 30.4 (2017): e3601.
  14. Ros, C., et al. "Reconstruction of phase images for GRAPPA based susceptibility weighted imaging (SWI)." Proceedings of the 16th Annual Meeting of ISMRM, Toronto, Canada. 2008.
  15. Ros, Christian, et al. "Reconstruction of phase images for GRAPPA accelerated Magnetic Resonance Imaging." 4th European Conference of the International Federation for Medical and Biological Engineering. Springer, Berlin, Heidelberg, 2009.
  16. Parker, Dennis L., et al. "Phase reconstruction from multiple coil data using a virtual reference coil." Magnetic resonance in medicine 72.2 (2014): 563-569.
  17. Eckstein, Korbinian, et al. "Computationally efficient combination of multi‐channel phase data from multi‐echo acquisitions (ASPIRE)." Magnetic resonance in medicine 79.6 (2018): 2996-3006.
  18. Buehrer, Martin, Peter Boesiger, and Sebastian Kozerke. "Virtual body coil calibration for phased-array imaging." Proceedings of the 17th Annual Meeting ISMRM. 2009.
  19. Roemer, Peter B., et al. "The NMR phased array." Magnetic resonance in medicine 16.2 (1990): 192-225.
  20. Walsh, David O., Arthur F. Gmitro, and Michael W. Marcellin. "Adaptive reconstruction of phased array MR imagery." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 43.5 (2000): 682-690.

Figures

Figure 1: Phased-array receivers produce an ellipse per channel in the complex plane. The GCC method leads to unpredictable combined phase-cycle points. The ellipse is mapped chaotically through the coil combination and the phase-cycle points show that a solution to the lGS does not exist for this pixel, i.e., there is no cross-point. The SMF preserves the elliptical model only after a phase-unwrapping step. The artifact at the bottom of the SMF ellipse is due to errors during phase-unwrapping.

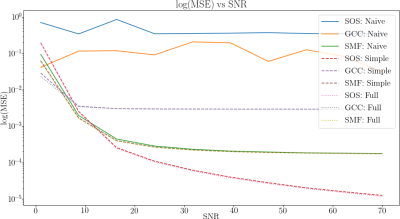
Figure 2: NRMSE plotted as a function of SNR using a logarithmic scale for prior coil combination with and without the proposed phase substitutions. SOS and GCC techniques greatly benefit from simple phase substitution and all coil combination methods benefit from the proposed methods. When the full composite ellipse is constructed, the quality of the reconstruction for the SOS coil combined images are superior to the SMF. SOS with the phase substitutions provide the best reconstruction in terms of raw NRMSE over the SNR range simulated.

Figure 3: Residual images for computer simulations run with SNR=47. At the bottom of each image the error along with a contrast factor that normalizes the error is shown. Reference is the single coil lGS with no additive noise. The columns are labeled according to the reconstruction method: “coil-by-coil” lGS, “naive” (the coil combination and lGS were performed without any phase substitutions), the proposed “full" phase substitution, and “simple”phase substitution. The proposed methods outperform the naive approach. The red arrow shows a singularity in the naive SOS residual.

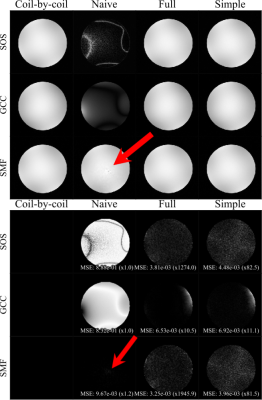
Figure 4: (Top) shows the results of the uniform phantom experiment. Naive and proposed methods are compared to the coil-by-coil lGS reconstruction. The red arrow shows an artifact due to phase discontinuity as the SMF may have artifacts from non-smooth phase while the proposed method exhibits no comparable artifacts. (Bottom) shows the residuals and NRMSE. The SOS and GCC produce images of unusable quality. Errors due to a phase singularity in the naive SMF can be seen. The full phase substitution provides the best performance with the simple substitution performing comparably.

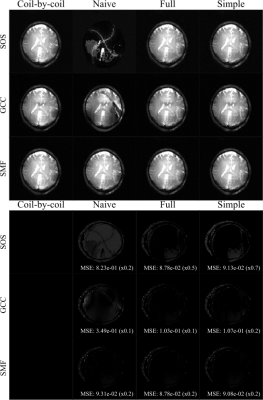
Figure 5: (Top) Results of the in vivo brain experiment. The naive and proposed methods are compared to the coil-by-coil lGS reconstruction. The columns are labeled according to the reconstruction method. The proposed methods clearly outperform the naive approaches for the SOS and GCC. (Bottom) Residual error showing NRMSE for the in vivo brain experiment. As expected, massive error is found in the naive SOS reconstruction where all phase information has been discarded. Performance of the naive GCC also matches that of the simulation and phantom experiments.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
0669