Introduction

Due to the long time taken by magnetic resonance imaging (MRI), voluntary or involuntary motion was usually inevitable during clinical examinations. Motion artifact deteriorates the quality of MRI. Shortening the image acquisition time is the most straightforward approach to reduce motion artifacts [1], so compressed sensing (CS) [2], as a popular method for acceleration of MRI acquisitions, can naturally be used to reduce motion artifacts. Recently, Convolutional neural networks (CNN) were proved to provide some motion mitigation, but blurring was introduced into the resulting images [3]. Here we combine the advantages of both CNN and CS to alleviate motion artifacts and obtain images with higher quality.

Methods

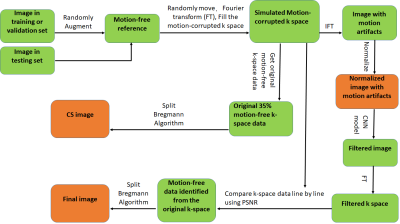
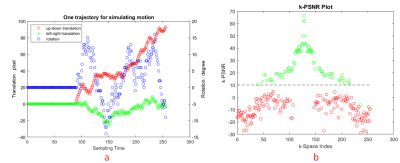
Simulated motion-corrupted images
The flowchart of our method was illustrated in Figure 1. We used the PD images from IXI data set (resolution=0.9735mmx0.9735mmx1.2mm) [4] to create simulated motion-corrupted images and their corresponding motion free images. We split the dataset into three datasets: training (9888 slices), validation (432 slices) and test (50 slices). Motion-corrupted k-space data was simulated using a random motion trajectory similar to the one shown in Figure 2 and using a pseudo Gaussian random sampling scheme typical in CS but extended to 100% sampling. Since our scheme uses CS to construct the final image, at least beginning 35% data should be motion free. Three motion trajectories with 35%, 40%, 50% motion-free k-space data were used in our experiments. Inverse Fourier transformed (IFT) was then applied to motion-corrupted k-space data to obtain images imposed by motion artifacts.
CNN model to filter images with motion artifacts
Firstly, images with motion artifacts were filtered by a CNN model based on U-Net [5] to get filtered images (Figure 3). To train the CNN model, simulated motion-corrupted images together with their corresponding motion-free reference images were used as input. The images in the training or validation set were augmented with random translation, rotating, scaling and shearing before they were used as reference images and to create simulated corrupted images. After the CNN model was properly trained, images in test dataset can be fed into it to create filtered images.
Detect lines influenced by motion in k-space
Filtered image was then Fourier transformed to k-space. Then the filtered k-space was compared with the original k-space line by line using peak signal to noise (PSNR) as quantitative criteria to detect lines influenced by motion.
Reconstruction of final images
Lines influenced by motion were removed from the original k-space, and the remaining data was reconstructed using split Bregman Algorithm [6]. The result was evaluated with PSNR and structure similarity (SSIM) and compared to the direct reconstruction using CS.

Results

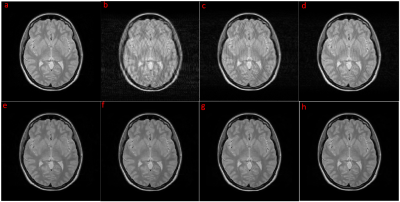
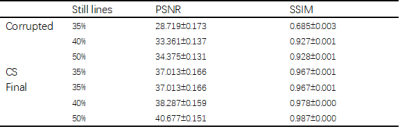
Comparison of filtered k-space with original k-space was shown in Figure 2(b). Final reconstructed images are shown in Figure 4. Table 1 lists the PSNR and SSIM values for the proposed algorithm together with those for the motion-corrupted images and images constructed using fixed 35% k-space data with CS. Since our approach detected almost all the k-space lines influenced by motion, it obtains the same result with CS on 35% data. However, when more motion-free k-space lines were detected, the result of our approach exceeded CS on 35% data.

Discussion

CNN model was used to map a motion-corrupted image to a motion-free image. Though the filtered image was far from perfect, compared with the corrupted image, it still looked more like the motion-free image. So, it is understandable its k-space was also similar to that of the reference image. Thus, k-space lines influenced by motion were more dissimilar to those of filtered k-space. This is our basic idea to use the filtered k-space to detect line influenced by motion. This is the major difference between our work and a recent study which using a motion estimation model to find corrupted lines [3]. From Figure 2(b), it can be seen clearly our approach can identify the corrupted lines with high precision, especially in the center of k-space. In future, more flexible sampling schemes can be designed to take advantage of this idea. For examples, k-space center can be repeated scanned in different time point to be used as probe for accurate detection of motion and eliminate the requirement of the patient keeping still in the first part of the scan.

Conclusion

Our approach can detect k-space lines influenced by motion and effectively remove motion artifacts from MRI images.

Acknowledgements

This project is supported by National Natural Science Foundation of China (61731009, 81771816).