Introduction

Differences in the magnetic field within a voxel result in dephasing and reduced signal. These differences within a voxel may stem from both local field inhomogeneity and induced inhomogeneity due to the imaging gradients, which interact by emphasizing or canceling each other. Even under no field inhomogeneities, imaging gradients in any gradient-encoded k-space imaging introduce dephasing which grows with increasing k-space encoding and results in apodization in k-space and spatial blurring. Given a good estimation of the field inhomogeneity, these effects can be accounted for or mitigated by various approaches, such as modelling and oversampling in space or in time^[1-4]. As non-Cartesian trajectories are commonly acquired continuously, they are more susceptible to phase evolution, and subsequently, more effort has been put by research in this field to account for field inhomogeneity effects. Recently more research in Cartesian sampling has been focused on accounting for phase evolution and signal decay - resulting in new acquisition schemes in concert with tailored reconstruction. We focus here on corrections for field inhomogeneity gradients in Cartesian sampling patterns, clarifying its implications to trajectory design, and show results in 2 Cartesian cases - Echo-Planar Time-resolved Imaging (EPTI)^[5], which provides a series of images along the acquisition, and an ultra-high-resolution ex-vivo imaging utilizing long bipolar readout gradient.

Theory

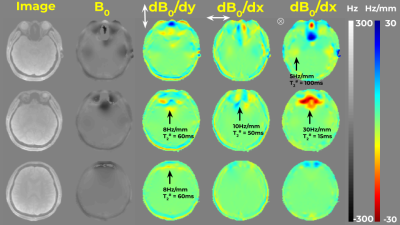
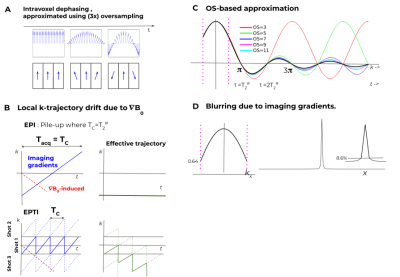
Figure 1 presents $$$B_0$$$ and $$$\nabla B_0$$$ for several slices of brain, 3T, with notable field inhomogeneities. To capture the effect of $$$\nabla B_0$$$ , we define $$${T_2^\#}_{x,y,z} := (1/\Delta) / (\partial B_0(r)/\partial \{x,y,z\})$$$, where $$$\Delta$$$ is the voxel size and $$$B_0$$$ is in Hz. Here $$$T_2^\#$$$ is the time evolution (e.g. in ms) to cause a 2𝜋 linear phase slope across the voxel, ie. complete dephasing (Fig. 2A right panel). For brain imaging at 3T at 2 mm resolution (Fig.1), $$$T_2^\#$$$ can be as short as ~30ms, implying a need to account for this effect in many typical imaging situations as illustrated in Fig.2B. Let $$$T_C$$$ be the time taken to cover k-space in a certain acquisition scheme. For EPI, $$$T_C=T_{acq}$$$ and when $$$T_2^\# =T_{acq}$$$ voxel pile-up occurs between adjacent voxels. EPTI benefits both from the utilization of parallel-imaging for increased imaging gradients/BW, and a zigzagging k-t scheme with accounting for field inhomogeneity. Still, $$$T_2^\# \approx T_C$$$ implies a trajectory drift which will result in increasing partial coverage at later echoes, and signal loss (Fig. 2B).
Assuming piecewise linear field inhomogeneity and box-car shaped voxels, the signal stemming from a single voxel is $$$s(r,t)=\Pi_dsinc(k_d(t)+\partial B_0 /dr_d \cdot t)$$$ where $$$d$$$ goes over the 3 spatial dimensions. As this involves both the spectral and the image domain, fully accounting for this term demands intensive calculations. Oversampling was suggested as an approximation^[1-4]. Oversampling approximates the effects on a voxel as the sum of the effects on its partitions (Fig.2A). As the $$$T_{acq}>>T_2^{\#}$$$, higher oversampling is needed for accurate description (Fig.2C). Apodization due to imaging-gradients-induced dephasing and the resulting blurring is shown in Fig.2D.
For EPTI, Dong et al.^[6] suggested reconstruction by multiplying with a tensor including the $$$B_0$$$ derived phase evolution per each echo. Since very few (#shots) PE k-lines are acquired per-echo, the inclusion of the predefined interaction of the PE-axis inhomogeneity derivative per echo with the associate imaging gradient for the lines acquired can be done with an only #shots-times increase in tensor size, and without an FT. For a 2D-based sequence accounting for the thorough-slice dephasing can also be incorporated into the same tensor. For the RO direction, we have approximated the effects of dephasing as a product of the separate effects of the imaging and $$$\partial B_0/\partial RO$$$.

Methods

For EPTI, subspace-constrained reconstruction^[6,7] was augmented as described above. FOV=24cm, Martix=120x120, 3-shots with R=4.
Ex-vivo^[8]: Fully sampled GRE-ME with resolution=150um, long (6.3ms) RO gradients with alternating polarity across echoes. Cartesian time-segmentation was applied on the RO direction to account for the effects of field inhomogeneity.

Results

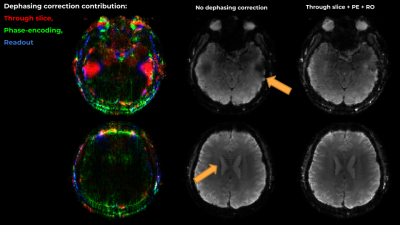
Figure 3 presents results on slices with artifacts due to through-slice dephasing and PE-direction inhomogeneity gradient induced dephasing. While the field inhomogeneity slope in PE is weaker, it results in visible model imperfection and striping artifacts, which can be much reduced. In the RO axis, accounting for inhomogeneity gradients resulted in a more complete representation of the skull, and increased sharpness due to the removal of the imaging-gradients induced apodization.

Figure 4 presents the effects of the suggested correction on 2 echoes from another representative slice. The corrections are more pronounced in the later echoes.
Figure 5 presents results on the ex-vivo data. Accounting for the field inhomogeneity induced phase evolution through Cartesian time-segmentation corrected misalignments, which allowed for multi-echo signal fitting, producing sharper, higher SNR image. $$$T_2^*$$$ map calculated after correcting the inhomogeneity-induced misalignments is more uniform and detailed.

Discussion and Conclusion

In-plane and through-plane intravoxel dephasing stemming from gradients in the field inhomogeneity in a common (healthy brain, 3T) settings result in artifacts and signal losses, under Cartesian acquisition schemes. Accounting for these, as for phase evolution effects, can be done in an efficient way and provides higher model accuracy and clearer images. This procedure is of increased significance in the frontal cortex and regions suffering artifacts in common EPI and even EPTI imaging, and in ultra-high-resolution applications.

Acknowledgements

This work was supported in part by NIH research grants: NIH R01EB019437, R01EB020613, R01 MH116173, and U01EB025162.