Introduction

A major challenge of ultra-high field MRI is the spatially inhomogeneous transmit (TX) radio frequency field ($$$B_1^+$$$) that induces spatial contrast variations. This problem has been addressed by combinations of multi-channel TX coils, spatial mapping of$$$\,B_1^+\,$$$or the flip angle (FA), and by $$$B_1$$$ shimming or parallel transmission^1,2. Mapping channel wise independent$$$\,B_1^+\,$$$maps over a 3D volume covering the human brain has been achieved by combining a single, absolute$$$\,B_1^+\,$$$map (e.g. acquired by the actual flip angle (AFI) technique³) with multiple relative maps⁴, or directly by other approaches such as DREAM⁵. In contrast, 3D mapping of$$$\,B_1^+\,$$$fields in the body is challenging, in particular due to respiration and specific absorption rate (SAR) limitations. Thus, several UHF body studies targeting the heart, aorta and other organs^6,7,8 have successfully applied a fast (breathold-long) and low power 2D technique, that derives proton-density biased, complex$$$\,B_1^+\,$$$maps from multiple gradient echo scans. The resulting relative$$$\,B_1^+\,$$$maps essentially miss a spatially constant scaling factor λ between such relative and absolute maps. Despite these limitations, the technique has proven to be highly suitable, even for parallel transmission in cardiac MRI⁷. The present work shows a novel, UHF$$$\,B_1^+\,$$$mapping technique that has three features: First, it extends the aforementioned method towards 3D$$$\,B_1^+\,$$$mapping for UHF body MRI; second it determines the scaling factor λ to obtain absolute B1+ maps and third, since the scan runs under free-breathing it yields multiple 3D $$$B_1^+$$$ maps of different respiratory states.

Methods

First,$$$\,K\times R\,$$$three-dimensional respiration-resolved relative $$$B_1^+$$$ maps $$$\,\widetilde{B_{1,k,r}^{rel}}\,$$$for each channel $$$k=1\ldots K$$$ and respiratory state $$$r=1\ldots R$$$ were derived using a technique similar to⁹. The tilde denotes, that maps are estimated/biased. To this end, a radial phase-encoded (RPE)^10,11 3D gradient-echo acquisition (RPE-GRE,cf. fig.1) was acquired$$$\,K\,$$$times and for each acquisition only one TX channel$$$\,k\,$$$transmitted while all others were inactive. The$$$\,K\times R=8\times10\,$$$gradient-echo (GRE) images$$$\,I_k\,$$$were reconstructed using self-navigation, retrospective respiratory binning (sliding window with 40% overlap) and NUFFT based on a k-t SENSE algorithm^11,12,13. Subsequently, individual maps $$ \widetilde{B_{1,k,r}^{rel}} = \frac{I_{k,r}}{(M_{z0}\sum_k\lvert I_{k,r}\rvert)^{\frac{1}{2}}} $$
were derived similar to⁹ with $$$M_{z0}$$$ proportional to proton density. Subsequently an RPE-based AFI^3,14 was acquired using a circular polarized (CP) mode$$$\,B_1^+$$$-shim yielding respiration-resolved absolute$$$\,B_1^+$$$ maps$$$\,B_{1,r}^{CP}$$$, which, however, exhibited local regions with low FA (<10degrees) that are excluded from further post processing. Such maps were merged with gradient-echo images resulting in absolute maps (with undefined regions) of channel$$$\,k$$$ and respiratory state$$$\,r$$$: $$$\widetilde{B_{1,k,r}^{abs}}=\frac{\lvert{I_{k,r}\rvert}}{\lvert{\sum_1^KI_{k,r}}\rvert}B_{1,r}^{CP}$$$ ⁴. Note, that$$$\,\lvert{\sum_1^KI_{k,r}}\rvert$$$ generates an image transmitted in CP mode. Finally the scaling factor $$$λ$$$ is calculated based on an ROI $$$\Gamma$$$ with high$$$\,B_1^+\,$$$amplitude revealing estimated, but absolute $$$B_1^+$$$ maps:$$$\widetilde{B_{1,k,r}^{abs}}=\lambda\cdot\widetilde{B_{1,k,r}^{rel}} $$$ with $$$\lambda = \frac{\widetilde{B_{1,k,r}^{abs}}}{\widetilde{B_{1,k,r}^{rel}}}\Bigg\rvert_{\Gamma}$$$.
All scans were performed at 7T (Magnetom 7T, Siemens, Germany) and in-vivo scans according to an approved IRB protocol. An initial phantom scan was performed using an 8-channel transceiver head coil using an agarose-water phantom ($$$σ=0.4\text{s}/\text{m},\, ε=79$$$) which performed a periodic ($$$f=0.15\text{Hz}$$$) translational movement in bore direction. The technique was evaluated at both extremal positions and resulting maps were compared to identical acquisitions with the phantom being static at those two positions. Five subjects were scanned using an 8-channel transceiver body coil. All reconstructed$$$\,B_1^+\,$$$maps were converted to FA maps for a reference voltage of$$$\,U_{ref} = 30\text{V}/\,160\text{V}\,$$$(phantom/in-vivo) and nominal FA = 60°/32°. Acquisition times of the RPE-GRE and RPE-AFI were 10.25 and 12.25min, reconstruction time was approximately 30min.

Results

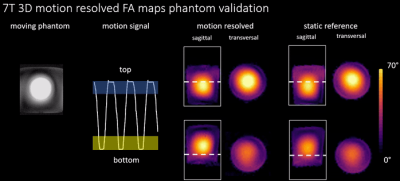
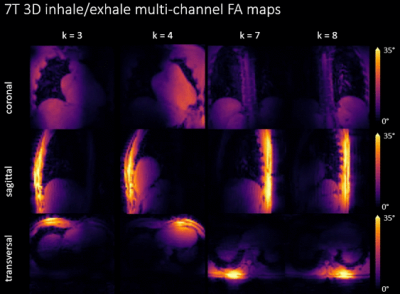
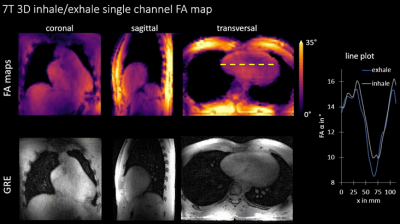
Fig.2 shows the derived phantom navigator signal and compares motion resolved 3D FA maps of two locations to a static reference measurement at same phantom locations. Quantitatively, the mean difference between static reference and dynamic measurement is$$$\,\overline{\Delta\alpha}=(0.8±12)°\,$$$(bottom) and$$$\,\overline{\Delta\alpha}=(-1.6±8)°\,$$$(top). Respiration-resolved in-vivo 3D FA maps from four out of the eight TX channels in one of the five subjects are illustrated in Fig.3. As can be seen, clean maps free from motion artifacts are obtained for the two motion states inhale and exhale. Fig.4, bottom displays RPE-GRE images obtained after homogeneous$$$\,B_1^+\,$$$shimming targeting the heart, which was performed in a single slice using an existing 2D mapping method as reported in⁷. The same shim set was retrospectively applied to the motion-resolved channel-wise FA data and the resulting FA maps after combining all TX-channels (Fig.4 top) which qualitatively agree with the obtained GRE images. Cross-sections of the FA distribution through the heart (dashed yellow line) for exhale and inhale demonstrate FA variations of up to 10% between both respiratory states, which agrees with previous work¹⁵.

Dicussion & Conclusion

In this work we present a novel technique to retrieve channel-wise, motion-resolved absolute 3D$$$\,B_1^+\,$$$maps of the human body at 7T. Although the maps inherently contain a proton density bias, similar non-respiration-resolved maps obtained in 2D have been successfully for cardiac PTX and other applications at 7T. Ideally, a direct merging of RPE-AFI and GRE-AFI is preferable, which was unfeasible because of insufficient B1+ amplitudes were present in the center of the body. The present method circumvents this limitation by using AFI data only in regions with high$$$\,B_1^+\,$$$amplitude for calibration purposes. Note, that the proposed method is not intended for online RF-pulse design, which is prevented by long acquisition and reconstruction times. Instead it allows acquiring libraries that can be used for offline RF pulse calculation¹⁶ including motion-robust RF pulses¹⁵.

Acknowledgements

Support of the German Research Foundation (DFG), project number GRK 2260, BIOQIC is acknowledged.