0658

Measurement and correction of spatiotemporal B₀ fluctuations using an FID-navigated EPI sequence

Tess E. Wallace^1,2, Jonathan R. Polimeni^2,3, Jason P. Stockmann^2,3, W. Scott Hoge^2,4, Tobias Kober^5,6,7, Simon K. Warfield^1,2, and Onur Afacan^1,2
¹Computational Radiology Laboratory, Boston Children's Hospital, Boston, MA, United States, ²Department of Radiology, Harvard Medical School, Boston, MA, United States, ³Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Boston, MA, United States, ⁴Brigham and Women's Hospital, Boston, MA, United States, ⁵Advanced Clinical Imaging Technology, Siemens Healthcare, Lausanne, Switzerland, ⁶Radiology, Lausanne University Hospital and University of Lausanne, Lausanne, Switzerland, ⁷LTS5, École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland

Synopsis

Spatiotemporal B₀ field fluctuations give rise to dynamic susceptibility-induced distortions in EPI time-series, which reduces signal stability, particularly at higher field strengths. In this work, we propose a novel method for rapid measurement of B₀ field changes from FIDnavs embedded in an EPI sequence. We demonstrate the ability of the proposed method to accurately characterize field changes up to second order in controlled phantom and volunteer experiments. Dynamic slice-wise distortion correction using FIDnav field estimates reduced normalized root-mean-square error and improved temporal SNR in volunteers performing deliberate arm motion.

Introduction

Single-shot EPI is widely used in functional and diffusion MRI studies, but suffers from susceptibility-induced geometric distortion. Static distortions can be corrected using a B₀ field map; however, this does not capture dynamic field variations that arise due to subject motion¹, respiration² and gradient heating³. Free induction decay navigators (FIDnavs) have previously been proposed to measure global frequency drifts in EPI time-series^4,5, but this is insufficient to compensate for distortions induced by spatially-varying field changes. In this work, we propose a novel method for rapid characterization of spatiotemporal B₀ fluctuations up to second order from FIDnavs using encoding information provided by a multi-channel reference image.

Methods

Theory. FIDnavs measure the integral of the excited spin distribution, modulated by field inhomogeneities and coil sensitivities at each spatial location⁶. This may be approximated by discrete summation of a complex multi-channel GRE reference image with matched contrast properties, acquired with reversed gradient polarities to compensate for gradient delays.

Dynamic changes in the B₀ field may be expressed as a series of low-order expansions over time: $$$\mathbf{\Delta{B_0^n}}=\mathbf{\Delta{B_0^0}}+\mathbf{\beta{b_n}}$$$,where $$$\mathbf{\Delta{B_0^0}}$$$ is the static field inhomogeneity, $$$\mathbf{\beta}$$$ represents spherical harmonic (SH) basis functions and $$$\mathbf{b_n}$$$ is a vector of the weighting coefficients at each time point $$$n$$$. A forward model can be generated by simulating the effect of changes in inhomogeneity coefficients on the complex FIDnav signals ($$$y_{j,n}$$$), with spatial encoding provided by the multi-channel reference image ($$$\bf{S_{j,0}}$$$):

$$\begin{bmatrix}y_{1,n}\\y_{2,n}\\.\\.\\y_{N_c,n}\end{bmatrix}=\begin{bmatrix}\bf{S_{1,0}}\\\bf{S_{2,0}}\\.\\.\\\bf{S_{N_c,0}}\end{bmatrix}\exp(i\gamma{T_{nav}}\mathbf{\beta}\bf{b_n})$$

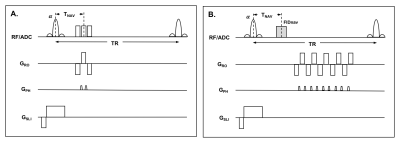
For a matrix size of 64x64 and TR of 2 s, GRE reference data for calibration would require ~4 minutes. This can be reduced to 1.2 minutes using a segmented EPI sequence with three readouts per TR and blip-up/blip-down encoding (Fig. 1A).

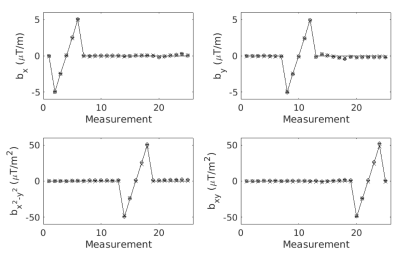
Phantom Validation. An FIDnav module was inserted between each slice-selective excitation and single-shot EPI readout (Fig. 1B). A water-bottle was scanned at 3T (MAGNETOM Trio; Siemens Healthcare, Erlangen, Germany) using a 32-channel head coil. First and second-order shim settings were systematically modified up to ±5 μT/m and ±50 μT/m². FID-navigated EPI (T_NAV=4 ms; TE=30 ms; TR=2 s; FA=90°; matrix=64x64; FOV=192 mm; 3-mm isotropic resolution; 10 slices; bandwidth=2232 Hz/px) and GRE field maps (TE₁/TE₂=4.92/7.38 ms; TR=300; FA=20°) were acquired for each shim setting. Changes in B₀ inhomogeneity coefficients up to second order were measured using a non-linear iterative algorithm⁷ to solve the inverse problem posed by the measured FIDnavs at each excitation.

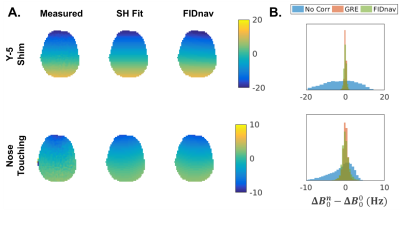
Volunteer Studies. Two subjects were scanned at 3T after providing written informed consent. Reference image data was acquired as described above. FID-navigated EPI scans (TE=30 ms; TR=2 s; FA=90°; matrix=64x64; FOV=224 mm; 3.5-mm isotropic resolution; 28 slices; bandwidth=2232 Hz/px; 10 repetitions) and ground-truth GRE field maps were acquired with changing the scanner Y-shim by 5 μT/m and while the volunteer touched their nose. FIDnav and GRE field estimates were converted into voxel-shift maps and normalized root-mean-square error (NRMSE) was calculated before and after distortion correction.

Since dynamic field changes influence the temporal stability of EPI, the efficacy of correction with our method was assessed in two volunteers imaged using an investigational whole-body 7T scanner (Siemens Healthcare). Dynamic EPI series (75 repetitions in 2.5 min) were acquired with no motion and with field changes induced by continuous hand-to-chin motion. Static and FIDnav-based dynamic distortion correction was applied to each EPI volume and temporal signal-to-noise ratio (tSNR) was computed following rigid-body registration to the reference volume.

Results

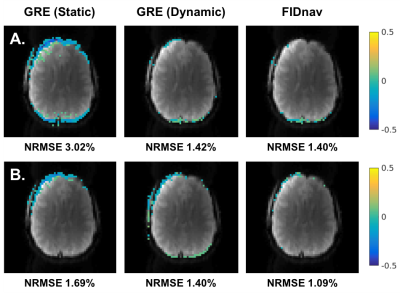
FIDnavs accurately characterized shim changes up to second order in the phantom (Fig. 2) with mean absolute errors of 0.053 ± 0.067 μT/m and 0.935 ± 0.984 μT/m².

Figure 3A shows a comparison of field changes ($$$\mathbf{\Delta{B_0^n}-\Delta{B_0^0}}$$$) measured using FIDnavs and dual-echo GRE in a volunteer. FIDnavs accounted for a substantial proportion of the variance induced by both manual shim changes and nose touching (Fig. 3B). FIDnav field measurements effectively corrected residual distortions (Fig. 4), with mean reductions in NRMSE of 56% ± 3% for changing Y-shim and 40% ± 7% for nose touching.

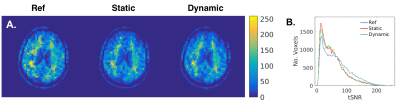
Figure 5 shows tSNR maps from a volunteer scanned at 7T. Across both volunteers performing the hand-to-chin motion, tSNR improved from 52.7 ± 1.4 to 54.8 ± 0.7 with FIDnav correction, compared to 60.6 ± 6.5 with no motion.

Discussion

Spatiotemporal B₀ fluctuations give rise to dynamic susceptibility-induced distortions in EPI time-series, which become particularly apparent with increasing field strengths. In this work, we demonstrate that FIDnavs can accurately characterize B₀ changes up to second order using the proposed method. Current state-of-the-art methods for dynamic distortion correction involve acquiring a dual-echo navigator image;⁸ however this requires ~1 second to acquire and process each volume. Our results show that FIDnav field estimates are in excellent agreement with measured dual-echo field maps in both phantom and volunteer experiments but take a fraction of the time to acquire. As FIDnavs can be inserted in each slice of the acquisition without disturbing the sequence, this facilitates continuous correction for spatiotemporal B₀ fluctuations, with potential for real-time dynamic shimming.⁹

Conclusion

Spatiotemporal B₀ variations up to second order can be rapidly and accurately characterized from FIDnavs embedded in an EPI sequence. The proposed approach facilitates slice-level dynamic distortion correction, which can be leveraged to improve the sensitivity of fMRI.

Acknowledgements

This research was supported in part by NIH grants R01 EB019483, R01 NS079788, R01 DK100404, R44 MH086984, IDDRC U54 HD090255 and P41 EB015896.

References

1. Liu, J., de Zwart, J. A., van Gelderen, P., Murphy-Boesch, J. & Duyn, J. H. Effect of head motion on MRI B0 field distribution. Magn. Reson. Med. 80, 2538–2548 (2018).

2. Van Gelderen, P., De Zwart, J. A., Starewicz, P., Hinks, R. S. & Duyn, J. H. Real-time shimming to compensate for respiration-induced B0 fluctuations. Magn. Reson. Med. 57, 362–368 (2007).

3. Foerster, B. U., Tomasi, D. & Caparelli, E. C. Magnetic field shift due to mechanical vibration in functional magnetic resonance imaging. Magn. Reson. Med. 54, 1261–1267 (2005).

4. Hu, X. & Kim, S.-G. Reduction of signal fluctuation in functional MRI using navigator echoes. Magn. Reson. Med. 31, 495–503 (1994).

5. Pfeuffer, J., Van de Moortele, P. F. De, Ugurbil, K., Hu, X. & Glover, G. H. Correction of physiologically induced global off-resonance effects in dynamic echo-planar and spiral functional imaging. Magn. Reson. Med. 47, 344–353 (2002).

6. Wallace, T. E., Afacan, O., Waszak, M., Kober, T. & Warfield, S. K. Head motion measurement and correction using FID navigators. Magn. Reson. Med. 81, 258–274 (2019).

7. Powell, M. J. D. The BOBYQA algorithm for bound constrained optimization without derivatives. (2009).

8. Alhamud, A., Taylor, P. A., van der Kouwe, A. J. W. & Meintjes, E. M. Real-time measurement and correction of both B0 changes and subject motion in diffusion tensor imaging using a double volumetric navigated (DvNav) sequence. Neuroimage 126, 60–71 (2016).

9. Stockmann, J. P. & Wald, L. L. In vivo B0 field shimming methods for MRI at 7 T. Neuroimage 168, 71–87 (2018).

Figures

Figure 1. Pulse sequence diagrams showing the segmented EPI acquisition used to acquire the reference image data (A) and FID-navigated single-shot EPI acquisition (B). The FIDnav module is inserted between the slice-selective excitation pulse and the EPI readout. The effective echo time of the reference acquisition is equal to the sampling time of the FIDnav (T_NAV), with all other imaging parameters held constant.

Figure 2. B₀ inhomogeneity coefficients measured in a phantom during manual modification of first-order (X and Y) and second-order (X²-Y² and XY) scanner shim settings. Solid line denotes applied shim currents; circles with error bars denote the mean and standard deviation of FIDnav B₀ inhomogeneity estimates; gray crosses denote results of directly fitting spherical harmonic functions up to second order to measured GRE field maps. FIDnavs embedded in the EPI sequence measure shim changes up to second-order with high accuracy using the proposed method.

Figure 3. Comparison of measured magnetic field changes (Hz) in an axial brain slice following modification of the Y-shim setting on the scanner by 5 μT/m and during nose touching (A). Residual B₀ field changes (B) with no correction (blue), ground-truth correction (red) and FIDnav correction (green). FIDnav estimates are in excellent agreement with results of direct SH fitting to measured field maps and account for a substantial proportion of the induced B₀ variance.

Figure 4. Differences in normalized signal intensity (>5%) between scans acquired after modifying the Y-shim setting by 5 μT/m (A) and during nose touching (B) following distortion correction of both scans using a static GRE field map (left); and with a dynamic GRE field map (middle) and FIDnav field estimates (right). The proposed method successfully reduces geometric distortion induced by shim changes and arm motion.

Figure 5. Temporal signal-to-noise ratio (tSNR) maps in a volunteer scanned at 7T with no motion (ref), and with repeated arm-to-chin motion with static and dynamic distortion correction (A). Histograms showing comparison of tSNR values in the masked region (B). A small improvement in tSNR is seen following dynamic distortion correction using second-order FIDnav B₀ field measurements.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

0658