Introduction

Conventional MR imaging uses linear B₀ gradients for spatial encoding, which have high cost and bulk, and lead to patient discomfort via acoustic noise and peripheral nerve stimulation. A few spatial encoding methods have been proposed that use RF gradient coils [1-4], which would not suffer the drawbacks of B₀ gradients, but these require linear RF amplitude or phase gradient coils or perform insufficient encoding. None enable quantitative MR imaging of T₁ and T₂ relaxation times. Here we propose a new RF spatial encoding method that combines B1⁺-selective excitations, MR fingerprinting (MRF) [5], and parallel transmission, to enable quantitative imaging.

Methods

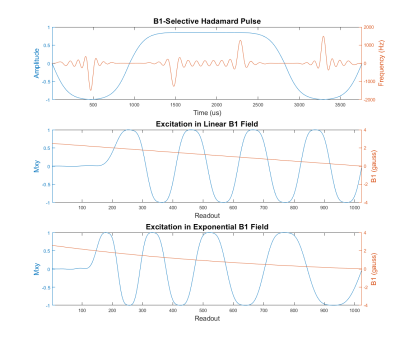
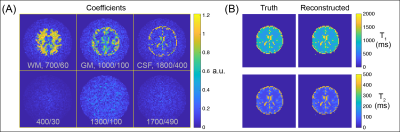
RF Pulse Design B₁⁺-Selective pulses were designed using the Shinnar-Le Roux algorithm [6], with a Hadamard beta filter design [7]. To mitigate distortions due to limited amplifier bandwidth in the experiment, the pulses’ original constant AM waveforms were tanh-modulated, and the FM waveforms were VERSE’d onto the modulated AM waveforms. Figure 1 plots a pulse designed for encoding 8 sub-slices, and the M_x profile it excites as a function of B₁⁺.

Barcoding Proof-of-Principle A simulation was performed using the B₁⁺/B₁^- maps of eight 15 cm-radius loops positioned circumferentially around a circular ROI. The maps were calculated by Biot-Savart, and the B₁⁺ maps were scaled to 0-10 Gauss inside the ROI. Then a set of 64 coil modes were defined, including individual coils and sums and differences of three and four coils. A set of 32 B₁⁺-selective Hadamard encoding excitation pulses (duration 3.8 ms) were designed to excite a slab between 0-8 Gauss with 32 sub-slices. A second set was designed with a half-slice shift, for a total of 64 pulses. This 64x64 = 4096 set of excitations were then used in an MRF Bloch simulation (TR = 4 ms, 2.5 cycles sinusoidal flip angle variation up to 90 degrees, inversion prep) to generate a dictionary of signal time courses at each spatial location for white matter (WM; T₁/T₂ = 700/60 ms), grey matter (GM; T₁/T₂ = 1000/100 ms), and cerebrospinal fluid (CSF; T₁/T₂ = 1800/400 ms), as well as three confounding signals with T₁/T₂ = 400/30, 1300/100, and 1700/490 ms. Brain WM, GM, and CSF masks and random noise were then used to generate signals for each receiver coil, and reconstruction was performed by dictionary matrix inverse.

Encoding Pulse Validation Experiment To validate the B₁⁺-selective Hadamard encoding pulses, a set of pulses were designed for 8 sub slices (Figure 1) to encode the long axis of a 10 cm-long mineral oil test tube phantom containing stacked circular disks at different radial positions (Figure 5, top). The sub slices were 0.25 gauss in width and spaced evenly between 0 and 2 Gauss. Data were acquired using a Tecmag Redstone MRI Console (Tecmag, Houston, Texas) with a single-turn 10 cm loop TR coil on a 47.5 mT whole-body permanent magnet. A 3D gradient-recalled echo sequence with a 10us hard pulse excitation was used to acquire reference images with parameters: TR = 75 ms, TE = 26 ms, Readout Bandwidth = 5 kHz, 128 readout points, and 31 by 31 phase encodes. This 3D scan was repeated using each Hadamard pulse for excitation, and the DC data were used to reconstruct the Hadamard-encoded images. A reference test tube phantom without structure was also excited with each Hadamard pulse to measure a calibrated reconstruction matrix.

Results

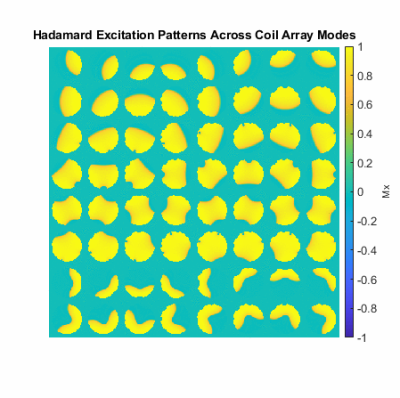
Barcoding Proof-of-Principle The GIF in Figure 2 shows the excitation patterns produced by each encoding pulse and mode. The patterns produce 0/pi phase oscillations over the excited slabs, with varying sub-slice widths, positions, and curvatures. Figure 3 shows signal correlation maps for four voxels at different radial and angular positions in the circular ROI, which reflect fine encoding resolution near the coils, where the B₁⁺ fields change the fastest and the B₁^- fields overlap the least. Resolution in the middle can be improved by increasing the number of excited sub-slices or adding excitations with sub-slice shifts. Figure 4 shows reconstructed coefficient and T₁/T₂ maps. Only one voxel inside the brain was misclassified.

Encoding Pulse Validation Experiment The phantom and coil setup for the experiment are shown at the top of Figure 5. The second row shows the hard pulse-excitation images that were obtained by summing images through the Hadamard-encoded slice widths. The third row shows the Hadamard-encoded images, which agree with the hard pulse images and have higher signal at deeper slices due to the uniform flip angles excited by the B₁⁺-selective pulse.

Conclusion

MR Barcoding was introduced as a new encoding technique based on non-linear RF magnitude gradients synthesized by an array of conventional transmit coils, combined with B₁⁺-selective Hadamard encoding pulses. Since it does not use B₀ gradients, it would be silent. It has low RFPA bandwidth requirements, so it could be implemented with low-cost on-coil amplifiers [8]. It could be applied to achieve large cost reductions in very low field systems, or to enable much larger (~1 m-wide) bores at high field. A proof-of-principle simulation showed that a 64x64 image could be reconstructed using an MRF model and a sub-30s scan duration. Experimental results validated the encoding capabilities of the B₁⁺-selective Hadamard encoding pulses.

Acknowledgements

This work was supported by NIH Grant R01 EB 016695.