0609
Time-optimized universal non-selective pulses for 7T MRI with parallel transmission1Institut Elie Cartan, Université de Lorraine, Vandoeuvre-lès-Nancy, France, 2Neurospin, CEA Saclay, Gif-sur-Yvette, France, 3INRIA Nancy Grand Est, Vandœuvre, France
Synopsis
Parallel transmission is a promising technology in high field MRI to mitigate the RF field inhomogeneity problem. In that context, the so-called Universal kT-point technique proves useful to achieve uniform spin excitation at no cost in terms of radio-frequency field calibration, although localized artefacts can occasionally appear due to the presence of very large resonance frequency offsets. By exploring more general RF pulse and magnetic field gradient waveforms than kT-points, this work introduces time-minimized universal pulses presenting better broadband behavior. In-vivo acquisitions on 5 volunteers at 7T have been performed to demonstrate the improvements.
Introduction
Parallel transmission (pTX) together with the universal pulse (UP) approach have demonstrated their potential to counteract the RF field inhomogeneity problem in high field head MRI with no need for subject-based calibration1,2. A package called PASTEUR3 exploiting kT-point UPs4, and providing MPRAGE, SPACE, FLAIR, DIR and GRE 3D sequences has been developed to enable 7T MRI brain examinations with greatly improved excitation uniformity as compared to the standard CP excitation mode. However, due to the presence of very large resonance offsets, especially in the vicinity of air tissue interfaces, the kT-point approach is not entirely immune to localized off-resonance-induced artefacts (e.g. at the sinus). It is proposed in this work to switch to a more general pulse design approach based on the Gradient Ascent Pulse Engineering (GRAPE) technique5, whereby the RF and gradient waveforms are both applied and optimized simultaneously. That approach suppresses the time needed for the gradient blips of kT-point pulses, and allows boosting the bandwidth of the pulses. These pulses are thus referred here as Time Optimized Pulses (TOP). The superior performance is illustrated with Bloch simulations and in vivo experiments on 5 volunteers at 7T.Method
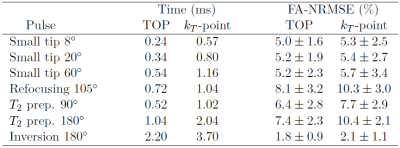
All acquisitions were performed on a 7T Siemens (Siemens Healthcare, Erlangen, Germany) equipped with the Step 2.3 pTX hardware and the Nova (Nova Medical, Wilmington, MA, USA) 8Tx-32Rx head coil. Universal TOPs were designed on the database of 20 brain field maps (ΔB0 and transmit B1 maps) used for PASTEUR. Our GRAPE implementation consists in discretizing the RF and gradient waveforms with small time steps (10 µs) and optimizing the value of the RF and gradient waveforms at all times using the second order Active-set algorithm of Matlab optimization toolbox. Explicit constraints were added to ensure that the solution satisfied the peak amplitude (165 V per TX channel), average power (1.5 W per channel and 8 W total), gradient slew rate (180 mT/m/ms) and gradient maximum amplitude (40 mT/m) constraints. The Flip Angle Normalized Root Mean Square Error (FA-NRMSE) was used as the objective function to minimize. For comparison with the PASTEUR kT-point UPs, the objective was to design TOPs that reach approximately the same FA-NRMSE as their kT-point counterparts but with minimum pulse duration. Firstly, Bloch simulations were performed on one subject field map to study the potential time gain. Then, a total of 7 universal pulses were optimized. The first 3 were scalable small FA pulses and were suitable to create uniform excitations with a FA up to 8°, 20° and 60°. The 8° TOP was designed for the MPRAGE and the GRE sequences while the others were incorporated in the GRE sequence only. A scalable 105° pulse was also designed in order to make a refocusing pulse train of variable flip angles for SPACE, FLAIR and DIR sequences7. The FLAIR sequence included a T2-preparation module that contained 90° and 180° pulses, whereby the 180° was simply obtained by concatenation of twice the 90° TOP°6. An additional inversion pulse was designed for the MPRAGE and the DIR sequences. The MPRAGE, SPACE, FLAIR and DIR sequences were applied on 5 healthy volunteers with the kT-points and with the TOPs in order to compare the two methods.Results
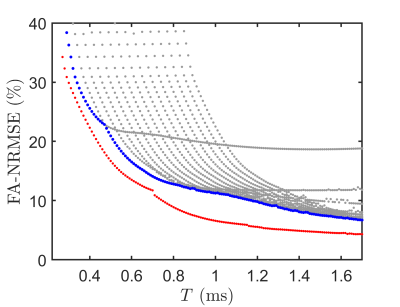
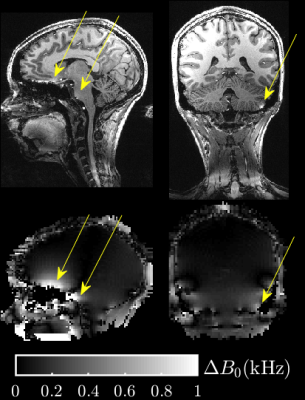
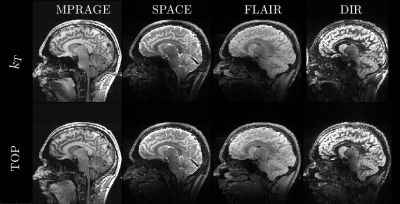
The TOPs were 31% to 57% shorter than the kT-points of the PASTEUR package, with similar FA-NRMSE, as shown in Table 1. Fig. 1 shows, for the kT-point pulse parameterization and for the TOPs, the FA-NMRSE dependence with the pulse duration T evaluated on one field map. Fig. 2 illustrates, for one MPRAGE acquisition with the kT-point UP, the occasional artefacts and the co-localized large B0 offsets causing a lack of efficiency in the sinuses, the pons and the cerebellum. Fig. 3 shows the results of the MPRAGE, SPACE, FLAIR and DIR sequences for both the TOPs and kT-points for one subject, showing good RF inhomogeneity mitigation in general for both cases. Fig. 4 emphasizes the gains obtained with the TOPs versus the kT-points with the MPRAGE and the DIR sequences, showing a great reduction of the occasionally remaining artefacts thanks to the decreased durations of the TOPs.Conclusion
We have presented a new application of the GRAPE technique to design non-selective UPs reducing pulse duration, at no expense in global FA homogeneity while still satisfying the same power limits. The larger bandwidth of TOPs as compared to kT-points allows improving the quality of the spin excitation at the locations of strong off-resonance offsets. In the current implementation, designing TOPs is computationally much more extensive than designing kT-points but this is not regarded as a major issue as long as universal solutions are targeted. For the inversion pulse used in MPRAGE and DIR, it appears that the frequency bandwidth of the pulse is still too low to completely remove the susceptibility artefacts. Decreasing further the duration would impose increasing the NRMSE. Alternatively, other metrics could be used to attempt increasing the pulse bandwidth locally where large off-resonances occur.Acknowledgements
This research has received funding from the ANR project QUACO (QUAntum COntrol: PDE systems and MRI applications) PRC ANR-17-CE40-0007-01, and the ERPT equipment program of the Leducq Foundation.References
1. Gras V, Vignaud A, Amadon A, et al., Universal pulses: A new concept for calibration-free parallel transmission, Magn Res Med. 2017;77: 635-643.
2. Gras V, Boland M, Vignaud A, et al., Homogeneous non-selective and slice-selective parallel-transmit excitations at 7 Tesla with universal pulses: A validation study on two commercial RF coils, PLoS One 2017; 12:e0183562.
3. Gras V, Mauconduit F, Vignaud A, et al., PASTeUR: Package of Anatomical Sequences using parallel Transmission UniveRsal kT-point pulses, in ISMRM 27th annual meeting & exhibition, Montréal, 2019.
4. Cloos M. A, Boulant N, Luong M, et al., kT-points: Short three-dimensional tailored RF pulses for flip-angle homogenization over an extended volume, Magn Res Med. 2012; 67:72-80.
5. Khaneja N, Reiss T, Kehlet C, et al., Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms, J Magn Res. 2005;172:296-305.
6. Gras V, Pracht E. D, Mauconduit F., et al., Robust nonadiabatic T2 preparation using universal parallel-transmit kT-point pulses for 3D FLAIR imaging at 7T, Magn Res in Med. 2019; 81:3202-3208.
7. Gras V, Mauconduit F, Vignaud A, et al., Design of universal parallel‐transmit refocusing kT‐point pulses and application to 3D T2‐weighted imaging at 7T, Magn Res Med. 2017; 80:53-65.
Figures