0607
Direct Saturation Control for Magnetization Transfer Imaging at 7T1Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2MR Research Collaborations, Siemens Healthcare Limited, Frimley, United Kingdom, 3Siemens Healthcare GmbH, Erlangen, Germany, 4Centre for the Developing Brain, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom
Synopsis
Systems with Magnetization Transfer (MT) are particularly sensitive to $$$B_1^+$$$ inhomogeneity, as the semisolid magnetization saturation is proportional to the square of $$$B_1^+$$$. This can be problematic at 7T imaging, where $$$B_1^+$$$ inhomogeneity is more severe, compromising the MT contrast obtained. This work proposes applying a composite MT prep-pulse with varying RF complex weights for each sub-pulse. These weights are optimized to deliver in the end a homogenous $$$\langle{}B_1^{+2}\rangle$$$, such that the MT contrast obtained is spatially uniform. Simulation and phantom results showed great improvement in the $$$\langle{}B_1^{+2}\rangle$$$ and MT ratio maps.
Introduction
A common method for producing Magnetization Transfer (MT) contrast in tissues with a semisolid proton fraction is to apply off-resonant RF irradiation to saturate their magnetization. The amount of saturation depends on the RF power applied off-resonance. At 7T the high degree of RF magnetic field ($$$B_1^+$$$) inhomogeneity causes saturation to be highly non-uniform spatially because RF power depends on the square of $$$B_1^+$$$. Parallel transmit (pTx) offers additional control of $$$B_1^+$$$ by creating a field that is the linear superposition of different transmit channels. Standard pTx RF pulse design methods1 are not suitable for designing pulses with uniform saturation properties because they optimize for rotation, not saturation. In this work we propose a pulse design framework for directly homogenizing RF saturation power using pTx, allowing Direct Saturation Control (DSatC) to obtain a more uniform MT contrast.Theory
Under the small tip angle approximation, the magnetization achieved by a saturation pulse in a parallel transmit system (pTx) is given by1:$$m(\mathbf{x})=\imath\gamma{}m_0\sum_{j=1}^{N_{coils}}s_j(\mathbf{x})\int_{0}^{\tau_{sat}}b(t)e^{\imath\mathbf{x}\cdot{}\mathbf{k}(t)}dt\qquad[1]$$
In a two-pool system, the magnetization vector from free water ("f") is extended to include a semisolid compartment ("s") such that $$$\vec{M}=[M_x^f M_y^f M_z^f M_z^s]^\mathsf{T}$$$. Evolution is described by the Bloch-McConnell (BM) equations:$$\frac{d\vec{M}}{dt}=\begin{bmatrix}-R_2^f&&\gamma\Delta{}B_0&&-\gamma{}B_{1,y}&&0\\-\gamma\Delta{}B_0&&-R_2^f&&\gamma{}B_{1,x}&&0\\\gamma{}B_{1,y}&&-\gamma{}B_{1,x}&&-R_1^f-k_{fs}&&k_{sf}\\0&&0&&k_{fs}&&-R_1^s-k_{sf}-W\end{bmatrix}\vec{M}+\begin{bmatrix}0\\0\\R_1^f\\R_1^s\end{bmatrix}M_0\qquad[2]$$$$W=\pi\gamma^2{B_1^{+2}g(\Delta})\qquad[3]$$
where the pulse is applied at off-resonance frequency $$$\Delta$$$ and $$$g(\Delta)$$$ is the absorption lineshape. No transverse magnetization is considered for the semisolid pool due to its very short $$$T_2$$$ ($$$\approx{}10\,\mathrm{\mu{}s}$$$). The key consideration for pulse design is that the lack of transverse components means that the semisolid magnetization does not see any applied gradients.
From [2] and [3], it is the $$$B_1^{+2}$$$ of the saturation pulse that governs the longitudinal magnetisation of the semisolid:$$B_1^{+2}(\mathbf{x},t)={\left\lvert{}\sum_{j=1}^{N_{coils}}s_j(\mathbf{x})b_j(t)\right\rvert{}}^2\qquad[4]$$
where $$$b_j$$$ are different RF pulse waveforms to play on each channel. The effect of the RF pulse can be found by integrating [2] over time; the method proposed for "pulsed" sequences (i.e. short RF pulses)2 is to consider the average saturation:$$\langle{}B_1^{+2}\rangle(\mathbf{x})=\frac{1}{\tau_{sat}}\int_{0}^{\tau_{sat}}B_1^{+2}(\mathbf{x},t)dt\qquad[5]$$such that an average saturation rate $$$\langle{}W\rangle$$$ can be applied over the duration of a whole pulse.
The method can further be simplified in the case that the overall RF pulse is made up of a train of $$$N_{sp}$$$ identical sub-pulses $$$b$$$ that are individually weighted (Figure 1). In this case the overall $$$\langle{}B_1^{+2}\rangle$$$ is determined by:$$\langle{}B_1^{+2}\rangle(\mathbf{x})=\frac{1}{N_{sp}}\sum_{i=1}^{N_{sp}}{\left\lvert\sum_{j=1}^{N_{coils}}s_j(\mathbf{x})w_{ij}\right\rvert}^2\langle{}b^2\rangle\qquad[6]$$where $$$w_{ij}$$$ is the complex weight applied to the $$$i^{th}$$$ sub-pulse and the $$$j^{th}$$$ transmit channel.
Uniform saturation power can be obtained by solving the RF optimization problem:$$w_{ij}^{opt}:=\underset{w_{ij}}{\arg\min}\,{\left\lVert\langle{}B_1^{+2}\rangle(\mathbf{x})-\mathrm{Target}\right\rVert}^2\qquad[7]$$subject to peak power, SAR, and average power constraints, where the target defines the desired $$$\langle{}B_1^{+2}\rangle$$$.
Methods
Experiments were performed on a 7T scanner (MAGNETOM Terra, Siemens Healthcare, Erlangen, Germany) in prototype research configuration, with an 8-Tx-channel head coil (Nova Medical, Wilmington MA, USA) using a prototype MT-weighted spoiled gradient-recalled-echo sequence (SPGR). Two phantoms (cross-linked egg white albumin, and water) were scanned using different number of sub-pulses and both circular-polarized (CP) and optimized shimming settings for the saturation pulse. In all cases, readout pulse was performed in CP mode. For all experiments $$$b$$$ was a Gaussian waveform applied at $$$|mathrm{1.2\,kHz}$$$ off-resonance (time-bandwidth-product of 1.92). For implementation reasons the total duration of all sub-pulses was fixed at $$$\tau_{sat}=\mathrm{10\,ms}$$$; as $$$N_{sp}$$$ was increased, the duration of each individual sub-pulse was then $$$\tau_{sat}/N_{sp}$$$. $$$B_1^+$$$ mapping was done using a pre-saturation turbo-FLASH sequence3, prior to shim optimization.The complex weights were optimized for composite pulse, varying the number of sub-pulses from one to three for a homogeneous $$$\mathrm{Target}=16\,\mathrm{\mu{}T}^2$$$.
To visualize the MT effects, a reference SPGR image with no MT prep-pulse ($$$M_{ref}$$$) was acquired in order to calculate the Magnetization Transfer Ratio (MTR):$$\mathrm{MTR}(\%)=100\times\frac{M_{ref}-M_{sat}}{M_{ref}}\qquad[8]$$where $$$M_{sat}$$$ is the image acquired with the saturation pulse.
Bloch-McConnell simulations were performed using measured $$$B_1^+$$$ maps and optimized complex weights from the phantom scanning to reproduce the experimental findings.
Results
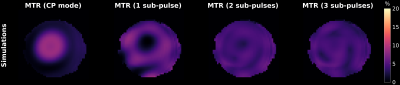
Figure 2 shows the $$$\langle{}B_1^{+2}\rangle$$$ of each sub-pulse for all optimized composite pulses, and the final $$$\langle{}B_1^{+2}\rangle$$$ achieved by each composite pulse, showing a decrease in the coefficient of variation (CoV) with increasing number of sub-pulses. Phantom scanning results (Figure 4) show that virtually no MT effects nor direct effect are observed in a water phantom, while in the MT phantom the MTR maps become more homogeneous for composite pulses with increasing number of sub-pulses. The Bloch-McConnell simulations (Figure 3) show a good agreement with the phantom results, especially for the CP mode and with 1 sub-pulse.Discussion and Conclusion
The optimization results showed that the $$$\langle{}B_1^{+2}\rangle$$$ produced by a composite pulse with more than one sub-pulse can deliver a much more homogeneous power distribution. The resulting improvement in uniformity of saturation was confirmed with phantom MTR measurements.Although other pTx based saturation pulse designs have been proposed in the past4,5 these still applied to systems with transverse magnetization, so gradients encoding could be employed. Our work aims to provide a framework for the design of uniform saturation of semisolids, which can only be influenced by spatial-temporal modulation of the $$$B_1^+$$$ field. Though this work demonstrates a "saturation only" design, composite pulse designs considering the effect on free water and semisolids together, effectively by jointly performing a classic RF shimming/pulse design with the $$$\langle{}B_1^{+2}\rangle$$$ optimization would be a generalized extension of this.Acknowledgements
This work was funded by the King’s College London & Imperial College London EPSRC Centre for Doctoral Training in Medical Imaging [EP/L015226/1] and supported by a Wellcome Trust Collaboration in Science Award [WT 201526/Z/16/Z] and the Wellcome/EPSRC Centre for Medical Engineering [WT 203148/Z/16/Z].References
1. Grissom W, Yip CY, Zhang Z, Stenger VA, Fessler JA, Noll DC. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn. Reson. Med. 2006;56:620–629 doi: 10.1002/mrm.20978.
2. Graham S, Henkelman, R. Understanding Pulsed Magnetization Transfer. J. Magn. Reson. Imaging. 1997; 7:903:912.
3. Fautz H P, Vogel M, Gross P, Kerr A, Zhu Y. B1 mapping of coil arrays for parallel transmission. Proc. Intl. Soc. Mag. Reson. Med. 16 (2008).
4. Tse DHY, Poser BA, Shah NJ. 1 Inhomogeneity Mitigation in CEST Using Parallel Transmission. 2017;2225:2216–2225 doi: 10.1002/mrm.26624.
5. Schneider R, Haueisen J, Pfeuffer J. Shaped Saturation with Inherent Radiofrequency- Power-Efficient Trajectory Design in Parallel Transmission. 2014;1027:1015–1027 doi: 10.1002/mrm.25016.
Figures
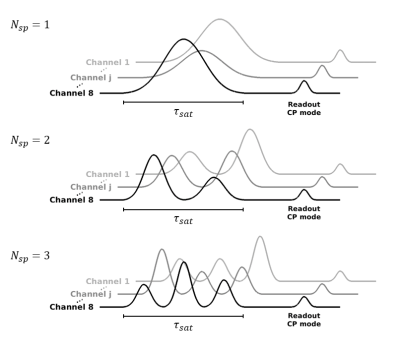
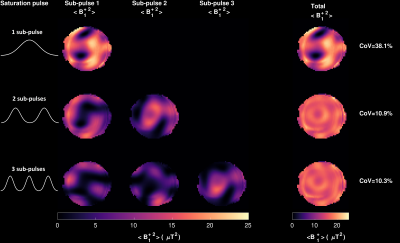
Figure 2: Optimized $$$\langle{}{B_1^{+2}}{}\rangle$$$ maps for each sub-pulse of several composite saturation pulses and their total $$$\langle{}{B_1^{+2}}{}\rangle$$$, where the coefficient of variation (CoV) represents the ratio between its standard deviation and the mean.