0604
Velocity encoded/compensated asymmetric multi-spoke RF pulses1Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany, 2Physikalisch-Technische Bundesanstalt (PTB), Braunschweig and Berlin, Germany
Synopsis
In this work, we investigate the feasibility of velocity encoded/compensated asymmetric multi-spoke RF pulses. Bloch simulations, phantom studies, and in-vivo measurements are conducted to characterize the pulse performance. Compared to conventional multi-spoke RF pulses, the results indicate that asymmetric multi-spoke RF pulses are suitable for both 2D and 3D acquisitions and can significantly reduce the repetition time without compromising on velocity quantification. The hereby gained acceleration can be additionally combined with techniques such as GRAPPA or compressed-sensing to further decrease the total acquisition time.
Introduction
It has been shown that time-resolved phase-contrast-based velocity quantification performed at 7T substantially benefits from a 2.2-2.6-fold SNR increase compared to 3T1,2, enabling isotropic spatial resolutions of 0.5mm in the brain at 7T. At 7T, however, significant variations in the transmit B1 field, particularly occurring when investigating the heart and great vessels, can impact velocity quantification3. In order to solve the latter problem, a variant of three-dimensional tailored “multi-spoke” RF pulses4-6 has been recently reported that allows for correct velocity quantification. Multi-spokes consist of a train of slice-selective RF pulses separated by small gradient pulses, and in the case of pTx, each spoke is applied with an individual B1+ shim setting.Two challenges exist when applying multi-spokes for velocity quantification/compensation. First, the inter-pulse duration between the RF pulses (ΔTE) has an impact on velocity-induced artifacts, and thus a minimal ΔTE is desired. Second, the total excitation duration increases, prolonging TR.
In this work, we investigate asymmetric multi-spoke RF pulses7 (asym-spokes) to address both issues. In general, asymmetric pulses (asym-pulses), which are typically generated by the Shinnar-Le-Roux (SLR) algorithm8, allow shorter TE and shorter TR than conventional sinc-shaped pulses. Here, we use asym-pulses for single- and multi-spoke excitation and compare their performance to a sinc-shaped pulse in the presence of flow. Since the asym-pulses generate a nonlinear phase along the slice, Bloch simulations and phantom measurements are performed to characterize their behavior under defined flow conditions and to evaluate the resulting slice profiles when applied in a multi-spoke fashion. Finally, the 2-spoke pulses are applied for in-vivo velocity quantification targeting the aorta at 7T.
Methods
An asym-pulse was compared to a Hanning-filtered sinc-shaped pulse (BWTP=7), both having a duration of 800µs (Fig.1A). Bloch simulations of an isochromat ensemble moving along the slice-selection axis with constant velocity were performed in MATLAB over a range of v=[-5:0.05:5]m/s for four different excitations: conventional and 2-spoke excitation using both sinc-shaped and asym-pulses. For the asym-2-spoke case, the second asym-pulse was reflected (see Fig.2D) to minimize ΔTE. The four excitations were implemented into a custom 4D flow sequence and applied at 7T (Magnetom 7T, Siemens, Germany). First, measurements were performed using a 28-channel knee coil (Quality Electrodynamics, USA) and an agarose-filled cylindrical phantom containing four pipes (diameters: 4.2/7.8/12.1/11.5mm) with water flowing through the two largest pipes. The slice profiles of all excitations were measured using a 3D acquisition corrected for coil sensitivities (parameters see Fig.3). Furthermore, velocity encoded 2D acquisitions were performed to evaluate the quantified velocities within three ROIs (50 repetitions were performed to improve statistical power). Then, in-vivo scans of a healthy volunteer targeting an axial slice of the ascending and descending aorta superior to the heart were performed according to an IRB-approved protocol using a custom-built 8-channel transceiver coil in pTx mode. The in-vivo measurements were performed using ECG gating and during breath-hold with parameters given in Fig.5.Results
The slice profile produced by the asym-pulse has a non-zero imaginary part (Fig.1B), which leads to 6% signal reduction due to through-slice dephasing for a 2D acquisition. By applying an asym-2-spoke excitation, consisting of an asym-pulse with a second but reflected asym-pulse, the imaginary part in the slice profile can be eliminated in the absence of flow (Fig.1C). However, if the relative scaling of the two asym-pulses' amplitudes is unequal, the slice profile still shows a residual imaginary part (Fig.1D). Fig.2 shows the results of the Bloch simulations for the investigated velocities. For physiologically relevant velocities (approx. 0-2 m/s), the asym-pulse’s slice profiles appear unaffected. In the asym-2-spoke case, the flow leads to a non-zero imaginary part of the slice profile, even if both asym-pulses are scaled identically, of up to 6% of the real part. The simulation results are supported by the measured slice profiles (Fig.3). The velocities quantified in the flow phantom (Fig.4) agree for all excitations within the three ROIs, and the maximum deviation between mean velocities obtained with different excitation schemes is 0.7cm/s. In-vivo results are shown in Fig.5 for 2-spoke excitations using sinc-shaped and asym-pulses, optimized for flip-angle homogeneity. Qualitatively, velocity maps during peak systole (Fig.5B-C) and time-resolved mean velocities (Fig.5D) agree. Quantitatively, the mean difference of the latter throughout the cardiac cycle was -1.4cm/s$$$\pm$$$5.5cm/s (Fig.5E) and the differences in peak velocity in the ascending and descending aorta were 9% and 2%, respectively. The temporal resolution was improved by using an asym-2-spoke excitation from 39.1ms to 33.9ms (13.3% reduction), while ΔTE was lowered from 2.8ms to 1.4ms.Discussion
In this work, we demonstrated the potential of velocity encoded/compensated asymmetric multi-spoke RF pulses that can be applied for velocity quantification in-vivo at 7T, in particular when targeting the heart or aorta. As shown here, asym-pulses can significantly reduce TR without compromising the velocity quantification. For 2-spoke excitations, the use of asym-pulses has the additional advantage of decreasing the inter-pulse duration, which is assumed to decrease flow-related slice profile degradation9. We conclude that asymmetric multi-spoke RF pulses are generally suitable for both 2D and 3D acquisitions; however, in the 2D case, the non-zero imaginary part along the slice profile generates a signal loss of up to 6%.Acknowledgements
No acknowledgement found.References
1. Hess AT, Bissell MM, Ntusi NAB, Lewis AJM, Tunnicliffe EM, Greiser A, Stalder AF, Francis JM, Myerson SG, Neubauer S, Robson MD. Aortic 4D Flow: Quantification of Signal-to-Noise Ratio as a Function of Field Strength and Contrast Enhancement for 1.5T, 3T, and 7T. Magnetic Resonance in Medicine 2015; 73(5):1864-1871.
2. van Ooij P, Zwanenburg JJM, Visser F, Majoie CB, vanBavel E, Hendrikse J, Nederveen AJ. Quantification and visualization of flow in the Circle of Willis: Time-resolved three-dimensional phase contrast MRI at 7 T compared with 3 T. Magnetic Resonance in Medicine 2013; 69(3):868-876.
3. Schmitter S, Schnell S, Ugurbil K, Markl M, Van de Moortele PF. Towards high-resolution 4D flow MRI in the human aorta using kt-GRAPPA and B1+shimming at 7T. Journal of Magnetic Resonance Imaging 2016;44(2):486-99.
4. Saekho, S., Yip, C.-y., Noll, D. C., Boada, F. E. and Stenger, V. A. (2006), Fast-kz three-dimensional tailored radiofrequency pulse for reduced B1 inhomogeneity. Magn Reson Med, 55: 719–724. doi: 10.1002/mrm.20840
5. Setsompop, K., Alagappan, V., Gagoski, B., Witzel, T., Polimeni, J., Potthast, A., Hebrank, F., Fontius, U., Schmitt, F., Wald, L. L. and Adalsteinsson, E. (2008), Slice-selective RF pulses for in vivo B1 image inhomogeneity mitigation at 7 tesla using parallel RF excitation with a 16-element coil. Magn. Reson. Med., 60: 1422–1432. doi:10.1002/mrm.21739
6. Schmidt, S., Flassbeck, S., Bachert, P., Ladd, M. E., Schmitter, S. (2019), Velocity encoding and velocity compensation for multi-spoke RF excitation. Magn. Reson. Imaging, in press
7. Cloos, M. A., Lee, W., Wiggins, G. C., Sodickson, D. (2013), Asymmetric Spokes: a demonstration of free-breathing pTX in the human torso at 7T. In Proceedings of the 21st Annual Meeting of the ISMRM, Salt Lake City, USA, 2012. Abstract 4258.
8. Pauly, J.M., Le Roux, P., Nishimura, D.G., Macovski, A. (1991), Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm. IEEE Trans. Med. Imaging 10, 53.65
9. Schmidt, S., Flassbeck, S., Breithaupt, M., Ladd, M. E., Schmitter, S. (2016), On the Performance of Multi-Spoke RF Pulses in the Presence of Laminar Flow - a Simulation Study. Magn. Reson. Mat. Phys. Biol. Med., 29(1 Supplement), 2016. ESMRMB 2016, 33rd Annual Scientific Meeting, Vienna, AT, September 29 - October 1, contribution no. 381.
Figures
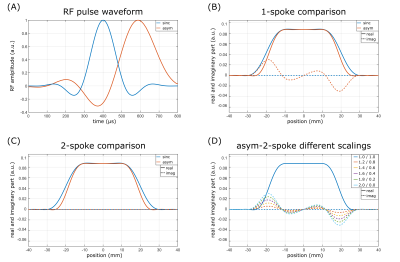
Figure 1:
A) RF waveforms of the sinc and the asym-pulse. B) The sinc pulse was chosen to match the slice profile created by the asym-pulse. C) Applying two asym-pulses (2nd pulse reflected) leads to a vanishing imaginary part of the slice profile and thereby to increased edge sharpness. D) If the amplitudes of the two asym-pulses are not equal, the resulting slice profile shows a non-zero imaginary part.
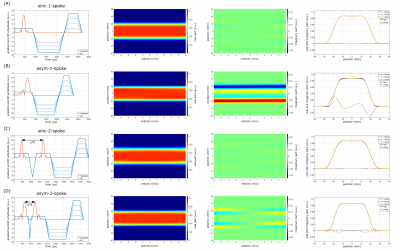
Figure 2:
Left: RF and gradient waveforms of the four different excitations (A-D). Note that the use of asym-pulses shortens the total duration needed for excitation and gradient rewinding.
Mid-left/Mid-right: Slice profile magnitude/phase as a function of velocity.
Right: Real and imaginary part of the slice profile for three example velocities.
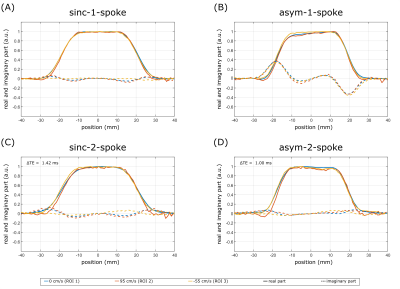
Figure 3:
Measured slice profiles for the different excitations. While sinc pulses do not show a difference between 1-spoke and 2-spoke excitation (A, C), the non-zero imaginary part in the asym-1-spoke case (B) vanishes for the asym-2-spoke excitation (D). Overall, the measured slice profiles fit the simulation results and no significant slice profile degradation due to flow is visible. Acquisition parameters: FOV=128x128x120mm³; resolution=1x1x1mm³; FA=5° (2.5°+2.5° for 2-spoke); TR=50ms; ΔTE according to the information in the figure.
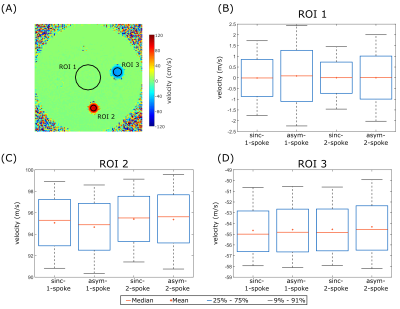
Figure 4:
Velocity quantification in the flow phantom using the four different excitation schemes. A) Example velocity map showing the flow phantom and the three ROIs used for the evaluation. The maximum deviations between the mean velocities obtained with the four different excitations for the three ROIs are 0.1cm/s (B), 0.7cm/s (C), and 0.3cm/s (D).
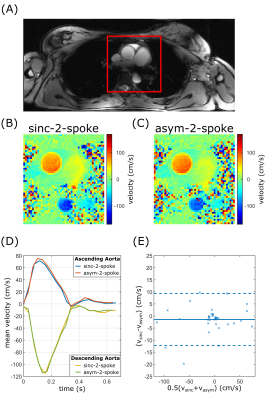
Figure 5:
A) Example timeframe of a 2D cine. B), C) Velocity maps in mid-systole of a 2-spoke excitation with sinc and asym-pulses, respectively. Note that B) and C) only show the image portion marked in A). D) Mean velocity in the ascending and descending aorta over the cardiac cycle with corresponding Bland-Altman plot E). The solid line indicates the mean value of -1.4cm/s and the dashed lines mark the 95% confidence interval. FOV=192x84x8mm³; res.=2x2mm²; slice thickness=8mm; GRAPPA=2; venc=170cm/s; pulse duration=800µs; acq. window=750ms; 2 lines per cardiac phase.