0602
On the Influence of Prior Knowledge in Learning Non-Cartesian 2D CINE Image Reconstruction1Department of Computing, Imperial College London, London, United Kingdom, 2School of Biomedical Engineering and Imaging Sciences, Kings College London, London, United Kingdom
Synopsis
In this work, we study the influence of prior knowledge in learning-based non-Cartesian 2D CINE MR image reconstruction. The proposed approach uses a novel minimal deep learning setup to embed the acquired non-Cartesian multi-coil data and conventional spatio-temporal (3D and 2D+t) Fields-of-Experts regularization in a proximal gradient variational network, achieving promising results for up to 12-fold retrospectively undersampled tiny golden-angle radial CINE imaging.
Introduction
Cardiac CINE MRI is the gold-standard technique for cardiac functional assessment. Parallel Imaging1-5 (PI) and Compressed Sensing6-9 (CS) reconstruction techniques have greatly enhanced image quality and reduced acquisition time for cardiac CINE imaging. Recently developed deep learning (DL) techniques have the potential to further reduce acquisition time and enable high-quality image reconstruction. However, many techniques require huge amounts of training data and complex network architectures with an enormous number of parameters, and are deployed regardless of available prior knowledge about the acquisition physics and the images themselves. Prior knowledge becomes even more important if only small amounts of data are available, as in cardiac MRI. In the field of dynamic MRI, mostly Cartesian undersampling was studied in a single-coil10,11 and multi-coil12 DL setting. Non-Cartesian undersampling strategies were used for 2D reconstruction13, as a post-processing network14,15 or formulated as deep image prior16.Tailored non-Cartesian undersampling strategies with golden-angle steps have been proposed to exploit both spatial and temporal redundancies in cardiac CINE MRI, but the reconstruction quality highly depends on the type of prior knowledge imposed within the reconstruction. In this work, we explore the influence of incorporating prior knowledge in learning-based reconstructions12,17. We show the performance of 3D and 2D+t regularization embedded in a novel Proximal Gradient Variational Network (PG-VN) for multi-coil tiny golden-angle radial18 cardiac CINE imaging.
Methods
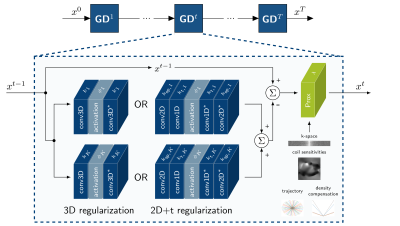
Proximal Gradient Variational Network (PG-VN)We consider the variational problem$$\min_x\frac{\lambda}{2}\Vert{Ax - y}\Vert^2_2+\mathcal{R}(x),$$to reconstruct the image$$$~x$$$ based on k-space data$$$~y$$$ using the non-Cartesian sampling operator$$$~A$$$, involving a non-uniform Fourier transform, undersampling trajectory, density compensation function and sensitivity maps. The regularizer$$$~\mathcal{R}(x)$$$ imposes prior knowledge on the reconstructions, and its strength is balanced by the parameter$$$~\lambda$$$. Above problem can be formulated as a learned VN12,17. In this work, we propose a PG-VN $$x^{t}=\text{Prox}_{\frac{\lambda}{2}\Vert{A\cdot-y}\Vert^2_2}(x^{t-1}-{\nabla}\mathcal{R}(x)).$$The proximal mapping is defined as$$x^{t}=\text{Prox}_{\frac{\lambda}{2}\Vert{A\cdot-y}\Vert^2_2}(\hat{x})=\arg\min_x\frac{1}{2}\Vert{x-\hat{x}}\Vert^2_2+\frac{\lambda}{2}\Vert{Ax-y}\Vert^2_2.$$However, no closed-form solution exists due to the structure of$$$~A$$$ and the proximal mapping has to be solved numerically19.
Using Fields-of-Experts17,20 regularization for$$$~\mathcal{R}(x)$$$, we obtain the PG-VN structure presented in Figure 1, involving complex convolutions, trainable non-linear activation functions and adjoint complex convolutions. In this work, we compare the impact of 3D and 2D+t complex convolutions. The 3D convolutions are performed with $$$k_\text{sp}{\times}k_\text{sp}{\times}k_\text{t}$$$ filters with spatial filter size$$$~k_\text{sp}$$$ and temporal filter size$$$~k_\text{t}$$$. For the 2D+t convolutions, we first apply spatial convolutions with $$$k_\text{sp}{\times}k_\text{sp}{\times}1$$$ filter, followed by temporal convolutions with $$$1{\times}1{\times}k_\text{t}$$$ filter. The same activation function$$$~\phi$$$ is applied to the real and imaginary part.
Data Acquisition and Processing
Eight short-axis slices of seven healthy subjects were scanned at 1.5T (Philips Ingenia) under breath-hold with a 2D radial bSSFP CINE. The acquisition parameters are as follows: Field-of-view$$${=}256{\times}256~\text{mm}^2$$$; resolution$$${=}2{\times}2~\text{mm}^2$$$; $$$8~\text{mm}$$$ slice thickness; TE/TR$$${=}1.16/2.30~\text{ms}$$$; tiny golden-angle radial18; 60º flip angle; 8960 k-space profiles acquired. Coil sensitivity maps were estimated using ESPIRiT21. The data were binned to $$$50~\text{ms}$$$ temporal resolution and different numbers of radial spokes were considered to achieve the desired retrospective undersampling factors for the individual experiments.
Experimental Setup
The PG-VN was trained for $$$T{=}5$$$ steps on 32 slices of size$$$~256{\times}256{\times}10$$$ from 4 different subjects using the ADAM optimizer with block pre-conditioning (1000 back-propagations) and a normalized mean-squared error $$$\min_{a,b}\frac{\Vert{ax+b–x_{\text{gt}}}\Vert^2_2}{\Vert{x_{\text{gt}}}\Vert^2_2}.$$$ We learned the weight$$$~\lambda>0$$$, activation functions based on linear interpolation ($$$N_w{=}31$$$) and $$$K{=}32$$$ 3D convolution kernels of size $$$5{\times}5{\times}3$$$ and 2D+t convolution kernels of size $$$5{\times}5{\times}1$$$ and $$$1{\times}1{\times}3$$$. This amounts to 5794 parameters for 3D regularization, and 2786 parameters for 2D+t regularization. The parameters were shared over the steps$$$~T$$$. Testing was performed on the remaining 3 subjects with full temporal coverage. The results were compared to inverse gridding, linear CG-SENSE1 and spatio-temporal TV6.
Implementation
Iterative schemes usually require a self-adjoint operator$$$~A$$$ fulfilling$$$~{\langle}Ax,y{\rangle}={\langle}x,A^*y{\rangle}$$$. Furthermore, a fast GPU implementation is required. The gpuNUFFT22 fulfills both conditions. We implemented a Python wrapper to use the gpuNUFFT in pytorch. This can be easily extended to other DL libraries such as tensorflow. For PI-CS, we used a spatio-temporal TV implementation23, which also requires gpuNUFFT22.
Results
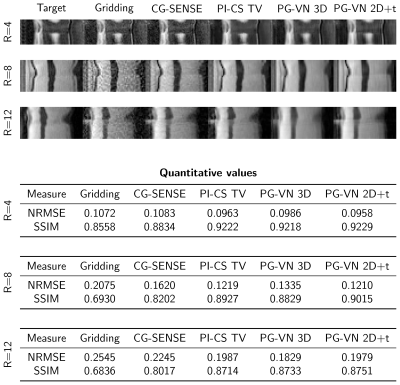
Qualitative results for 3 different cases and acceleration factors R=4,8,12 are shown in Figure 2-4. Time profiles along with quantitative values for the individual cases are depicted in Figure 5. CG-SENSE performs only slice-wise reconstruction and does not exploit any temporal redundancies. PI-CS TV performs well for R=4 and R=8, however, for R=12 it becomes more challenging to cope with the streaking artifacts. Additionally, we observe the typical block/staircasing artifacts. In all cases, we observe that PG-VN 3D introduces some blurring. For high acceleration factors (R=12), PG-VN 3D can deal better with the low contrast variation due to aliasing compared to all other approaches. PG-VN 2D+t has a much lower number of parameters and can exploit the spatio-temporal redundancies better than PG-VN 3D, resulting in more textured images. Similar observations are made for the time profiles.Discussion and Conclusion
In this work, we show the influence of 3D and 2D+t Fields-of-Experts regularization in a learning-based PG-VN reconstruction framework. Using a minimal PG-VN architecture, we achieve results on par with PI-CS by using prior knowledge from non-Cartesian sampling and complex 2D+t convolutions for the reconstruction of tiny golden-angle radial CINE MRI, even for higher acceleration factors. The results suggest incorporating even more available knowledge about the physics of data acquisition and improved spatio-temporal regularization in DL approaches.Acknowledgements
The work was funded by EPSRC Program Grant (EP/P001009/1).References
1. Klaas P. Pruessmann, Markus Weiger, Peter Börnert, Peter Boesiger. Advances in sensitivity encoding with arbitrary k‐space trajectories. Magnetic Resonance in Medicine, 46:638-651, 2001.
2. Hong Jung, Kyunghyun Sung, Krishna S. Nayak, Eung Yeop Kim,and Jong Chul Ye. k-t FOCUSS: A general compressed sensing framework for high resolution dynamic MRI. Magnetic Resonance in Medicine, 61(1):103-116, 2009.
3. Felix A. Breuer, Peter Kellman, Mark A. Griswold, Peter M. Jakob. Dynamic autocalibrated parallel imaging using temporal GRAPPA (TGRAPPA). Magnetic Resonance in Medicine, 53(4):981-985, 2005.
4. Peter Kellman, Frederick H. Epstein, and Elliot R. McVeigh. Adaptive sensitivity encoding incorporating temporal filtering (TSENSE). Magnetic Resonance in Medicine, 45(5):846-852, 2001.
5. Jeffrey Tsao, Peter Boesiger, Klaas P. Pruessmann. k-t BLAST and k-t SENSE: Dynamic MRI with high frame rate exploiting spatiotemporal correlations. Magnetic Resonancein Medicine, 50(5):1031-1042, 2003.
6. Ricardo Otazo, Daniel Kim, Leon Axel, and Daniel K. Sodickson. Combination of Compressed Sensing and Parallel Imaging for Highly Accelerated First-Pass Cardiac Perfusion MRI. Magnetic Resonance in Medicine, 64(3):767-776, 2010.
7. Ganesh Adluru, Suyash P. Awate, Tolga Tasdizen, Ross T. Whitaker, Edward V.R. DiBella. Temporally constrained reconstruction of dynamic cardiac perfusion MRI. Magnetic Resonance in Medicine, 57(6):1027-1036, 2007.
8. Li Feng, Monvadi B. Srichai, Ruth P. Lim, Alexis Harrison, Wilson King, Ganesh Adluru, Edward VR. Dibella, Daniel K. Sodickson, Ricardo Otazo, and Daniel Kim. Highly accelerated real-time cardiac cine MRI using k-t SPARSE-SENSE. Magnetic Resonance in Medicine, 70(1):64-74, 2013.
9. Michael Lustig, Juan M Santos, David L Donoho, and John Pauly. k-t SPARSE: High frame rate dynamic MRI exploiting spatio-temporal sparsity. In ISMRM 14th Annual Meeting, p. 2420, 2006.
10. Jo Schlemper, Jose Caballero, Joseph V Hajnal, Anthony N Price, and Daniel Rueckert. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Transactions on Medical Imaging, 37(2):491-503, 2017.
11. Chen Qin, Jo Schlemper, Jose Caballero, Anthony N Price, Joseph V Hajnal, and Daniel Rueckert. Convolutional recurrent neural networks for dynamic MR image reconstruction. IEEE Transactions on Medical Imaging, 38(1):280-290, 2018.
12. Kerstin Hammernik, Matthias Schloegl, Rudolf Stollberger, and Thomas Pock. Dynamic Multicoil Reconstruction using Variational Networks. In ISMRM 27th Annual Meeting, p.4297, 2019.
13. Jo Schlemper, Seyed Sadegh Mohseni Salehi, Prantik Kundu, Carole Lazarus, Hadrien Dyvorne, Daniel Rueckert, Michal Sofka. Nonuniform Variational Network: Deep Learning for Accelerated Nonuniform MR Image Reconstruction. In Medical Image Computing and Computer Assisted Intervention - MICCAI, pp. 57-64, 2019.
14. Andreas Hauptmann, Simon Arridge, Felix Lucka, Vivek Muthurangu, and Jennifer A. Steeden. Real‐time cardiovascular MR with spatio‐temporal artifact suppression using deep learning-proof of concept in congenital heart disease. Magnetic Resonance in Medicine, 81:1143-1156, 2019.
15. Andreas Kofler, Marc Dewey, Tobias Schaeffter, Christian Wald, Christoph Kolbitsch. Spatio-Temporal Deep Learning-Based Undersampling Artefact Reduction for 2D Radial Cine MRI with Limited Training Data. In IEEE Transactions on Medical Imaging, 2019.
16. Kyong Hwan Jin, Harshit Gupta, Jerome Yerly, Matthias Stuber, and Michael Unser. Time-Dependent Deep Image Prior for Dynamic MRI. arXiv preprint arXiv:1910.01684, 2019.
17. Kerstin Hammernik, Teresa Klatzer, Erich Kobler, Michael P. Recht, Daniel K. Sodickson, Thomas Pock, and Florian Knoll. Learning a variational network for reconstruction of accelerated MRI data. Magnetic Resonance in Medicine, 79:3055-3071, 2018.
18. Stefan Wundrak, Jan Paul, Johannes Ulrici, Erich Hell, Margrit‐Ann Geibel, Peter Bernhardt, Wolfgang Rottbauer, Volker Rasche. Golden ratio sparse MRI using tiny golden angles. Magnetic Resonance in Medicine 75:2372-2378, 2016.
19. Hemant Kumar Aggarwal, Merry Mani, and Mathews Jacob. MoDL: Model-based deep learning architecture for inverse problems. IEEE Transactions on Medical Imaging, 38:394-405, 2017.
20. Stefan Roth, Michael J. Black. Fields of Experts: A Framework for Learning Image Priors. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pp. 860-867, 2005.
21. Martin Uecker, Peng Lai, Mark J. Murphy, Patrick Virtue, Michael Elad, John M. Pauly, Shreyas S. Vasanawala, and Michael Lustig. ESPIRiT - an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic Resonance in Medicine, 71(3):990-1001, 2014.
22. Florian Knoll, Andreas Schwarzl, Clemens Diwoky, and Daniel K Sodickson. gpuNUFFT - An Open-Source GPU Library for 3D Gridding with Direct Matlab Interface. In ISMRM 23rd Annual Meeting, p.4297, 2014.
23. Matthias Schloegl, Martin Holler, Andreas Schwarzl, Kristian Bredies, and Rudolf Stollberger. Infimal convolution of total generalized variation functionals for dynamic MRI. Magnetic Resonance in Medicine, 78(1):142-155, 2017.
Figures