0601

A Novel Image Reconstruction Algorithm for Radial MRI Data Acquired with a Rotating Radio-frequency Coil (RRFC)
Andrew Phair1, Michael Brideson1, Jin Jin2,3,4, Mingyan Li2, Stuart Crozier2, and Lawrence Forbes1
1School of Natural Sciences, University of Tasmania, Hobart, Australia, 2School of Information Technology and Electrical Engineering, University of Queensland, Brisbane, Australia, 3ARC Training Centre for Innovation in Biomedial Imaging Technology, University of Queensland, Brisbane, Australia, 4Mark and Mary Stevens Neuroimaging and Informatics Institute, University of Southern California, Los Angeles, CA, United States

Synopsis

We present WARF, a novel reconstruction algorithm for radial MRI data acquired with a rotating radio-frequency coil (RRFC). The algorithm reconstructs each pixel as a weighted sum of all acquired data, with the weights determined by the k-space sampling pattern. The theory behind WARF leading to the derivation of appropriate weights is presented, and then WARF is applied to both simulated and experimental data sets. The results indicate WARF is achieving an improved robustness to RRFC angular velocity variability and k-space trajectory deviation compared with existing reconstruction methods.

Introduction

The rotating radio-frequency coil (RRFC) for MRI is an alternative to a multi-coil array that achieves sensitivity over the entire subject region through mechanical rotation during data acquisition whilst avoiding issues such as coil-size restrictions and fabrication complexity1-6. Recently, the RRFC has been combined with a radial k-space trajectory to allow self-calibration through oversampled k-space centres7. Ideally, the angular velocity and repetition time would be chosen to ensure that acquisitions occur at several discrete and equidistant coil positions, allowing the data to be treated as parallel array data. However, pneumatic actuation of the rotation results in variation in the angular velocity, and acquisition positions become dispersed. Jin et al.7 thus segmented spokes according to coil position, allowing segments of data to be treated as ‘pseudo-coils’ for parallel MRI reconstruction. Another approach, dynamic sensitivity averaging8, relies on the assumption that a relatively uniform net sensitivity profile is formed by the averaging of individual profiles, and reasons that by gridding with a large-enough kernel a net sensitivity-weighted image can be obtained. Both methods are sensitive to variation in coil velocity, and to deviation in k-space sample locations, caused by rapidly switching gradient coils. Herein, we present a weighted-sum approach to radial MRI image reconstruction with an RRFC (WARF), which produces good quality images while providing improved robustness to angular velocity variation and deviations in the k-space trajectory.

Method

We propose to calculate each of the $$$N$$$ pixels in the reconstruction, $$$\tilde{\rho}_n$$$, as a weighted sum of radial k-space samples $$$b_r$$$, $$\tilde{\rho}_n=\sum_{r=1}^Rw_{rn}b_r,$$ where $$$w_{rn}$$$ are weights that must be solved for. Each sample is allocated to one of $$$N_{c}$$$ pseudo-coils according to the coil position during acquisition, with $$$R_m$$$ points in the $$$m$$$th pseudo-coil. Utilising a discrete approximation, we write each k-space sample as the Fourier transform of the sensitivity-weighted image, $$b_r=\sum_{t=1}^{N}e_{rt}S^{(m_r)}_t\rho_t.$$ Here, $$$e_{rt}$$$ is a Fourier coefficient and $$$S^{(m_r)}_t$$$ is the sensitivity of the $$$m_r$$$th pseudo-coil at the $$$t$$$th pixel. Supposing the weights can be chosen such that $$L_{nt}=\sum_rw_{nr}e_{rt}=\begin{cases}1,&t=n\\0,&t\neq n\end{cases}$$ for every pseudo-coil, then the first two equations yield $$\tilde{\rho}_n=\sum_{t=1}^NL_{nt}U_t\rho_t=U_n\rho_n,$$ where $$$U_n$$$ is the net sensitivity at the nth pixel. Thus, finding weights to satisfy the $$$L_{nt}$$$ equation will yield an appropriate, sensitivity-weighted solution to the reconstruction problem. Applying a Tikhonov regularisation yields, for every pseudo-coil and every pixel, $$(E^*E+\lambda{I})\mathbf{w}_n=E^*\mathbf{L}_n,$$ where $$$E$$$ is an $$$N\times{R_m}$$$ matrix of Fourier coefficients, $$$\lambda$$$ is a regularisation parameter, $$$\mathbf{L}_n$$$ is zero vector with a 1 in the $$$n$$$th position and $$$\mathbf{w}_n$$$ is a vector containing weights for the $$$n$$$th pixel. This is a straightforward, albeit computationally expensive, equation to solve $$$N_{c}\times{N}$$$ times. However, as the weights depend only on the k-space sample locations, they can be stored and need not be recalculated for every scan.
WARF was implemented in MATLAB (MathWorks, USA) and applied to RRFC data simulated on an $$$804\times{134}$$$ radial trajectory, utilising a simulated sensitivity profile (Figure 1) produced with FEKO (Altair, USA) for a coil with diameter 40mm, length 25.5mm and open angle 60°. Using a homogenous phantom and a mouse head image, seventeen sets of simulations were performed; one with ideal parameters, eight using variable velocity profiles, and eight with deviated k-space trajectories.
The method was also applied to experimental scans of a shrew and a mouse acquired on a 9.4T Bruker BioSpec 94/30 pre-clinical MRI Scanner with a UTE sequence.
For comparison, four pre-existing reconstruction methods were applied to each data set.

Results

Figures 2 and 3 display the reconstructions for the ideal simulation, and one example each of a variable velocity and deviated trajectory simulation (corresponding to the velocity profile and trajectory in Figure 1). Figure 3 also displays the difference between the deviated trajectory reconstructions and the original image, clearly demonstrating WARF artefacts are of a lower magnitude than those of other methods. Mean square error (MSE) and structural similarity (SSIM), as compared to the sensitivity-weighted original image, are plotted for all seventeen simulations in Figure 4. These show WARF often outperforms the other methods and is particularly apt at supressing artefacts that result from trajectory deviations, achieving the lowest MSE value in every such simulation considered, along with the highest SSIM value in 11 of the 16 simulations. The reconstructions from the experimental scans are presented in Figure 5, where WARF reconstructions appear to have less artefacts than those from GRAPPA, SENSE and SENSE+L1, while being of similar quality to dynamic sensitivity averaging reconstructions.

Discussion

Reconstruction quality is affected by the parameter $$$\lambda$$$, with larger values resulting in reduced artefacts at the cost of additional smoothing. Here, a value of $$$\lambda=0.3$$$ has been used, but this can be adjusted depending on the relative importance of artefact suppression and image sharpness. Although WARF was designed for the radial RRFC imaging scheme described, this is not explicitly introduced into the underlying theory. Thus, future work will consider extending WARF to rotating arrays, stationary parallel MRI and arbitrary k-space trajectories.

Conclusion

We have introduced WARF, a new reconstruction algorithm for radial MRI with an RRFC, and demonstrated it for both simulated and experimental data sets, where it was seen to provide an improved robustness to variation in coil velocity and deviations in k-space sample locations.

Acknowledgements

This work was supported by the Australian Research Council Linkage Projects (LP120200375), an Australian Government Research Training Program (RTP) Scholarship, and was carried out using the Tasmanian Partnership for Advanced Computing high-performance computing clusters.

References

  1. Trakic, B. K. Li, E. Weber, H. Wang, S. Wilson, and S. Crozier, “A rapidly rotating RF coil for MRI,” Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering: An Educational Journal, vol. 35, no. 2, pp. 59–66, 2009.
  2. A. Trakic, E. Weber, B. K. Li, H. Wang, F. Liu, C. Engstrom, and S. Crozier, “Electromechanical design and construction of a rotating radio-frequency coil system for applications in magnetic resonance,” IEEE Transactions on Biomedical Engineering, vol. 59, no. 4, pp. 1068–1075, 2012.
  3. A. Trakic, J. Jin, M. Li, D. McClymont, E. Weber, F. Liu, and S. Crozier, “A comparative numerical study of rotating and stationary RF coils in terms of flip angle and specific absorption rate for 7 T MRI,” Journal of Magnetic Resonance, vol. 236, pp. 70–82, 2013.
  4. A. Trakic, H. Wang, E. Weber, B. Li, M. Poole, F. Liu, and S. Crozier, “Image reconstructions with the rotating RF coil,” Journal of Magnetic Resonance, vol. 201, no. 2, pp. 186–198, 2009.
  5. M. Li, J. Jin, A. Trakic, F. Liu, E. Weber, Y. Li, and S. Crozier, “High acceleration with a rotating radiofrequency coil array (RRFCA) in parallel magnetic resonance imaging (MRI),” in Engineering in Medicine and Biology Society (EMBC), 2012 Annual International Conference of the IEEE, pp. 1098–1101, IEEE, 2012.
  6. M. Li, Z. Zuo, J. Jin, R. Xue, A. Trakic, E. Weber, F. Liu, and S. Crozier, “Highly accelerated acquisition and homogeneous image reconstruction with rotating RF coil array at 7 T - A phantom based study,” Journal of Magnetic Resonance, vol. 240, pp. 102–112, 2014.
  7. J. Jin, E. Weber, Y. Tesiram, T. Hugger, M. Li, M. Fuentes, P. Ullmann, S. Stark, S. Junge, F. Liu, et al., “Image reconstruction for a rotating radiofrequency coil (RRFC) using self-calibrated sensitivity from radial sampling,” IEEE Transactions on Biomedical Engineering, vol. 64, no. 2, pp. 274–283, 2017.
  8. M. Li, E. Weber, J. Jin, T. Hugger, Y. Tesiram, P. Ullmann, S. Stark, M. Fuentes, S. Junge, F. Liu, et al., “Radial magnetic resonance imaging (MRI) using a rotating radiofrequency (RF) coil at 9.4 T,” NMR in Biomedicine, vol. 31, no. 2, p. e3860, 2018.

Figures

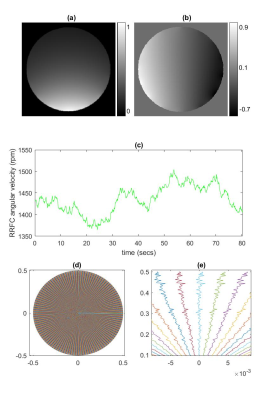
Figure 1: (a) Magnitude of coil sensitivity profile used in simulation. (b) Phase of coil sensitivity profile used in simulation. (c) Variable RRFC velocity profile for the simulations seen in the second rows of Figures 2 and 3. (d) Deviated k-space trajectory used for the simulations seen in the third rows of Figures 2 and 3. (e) A close-up view of the trajectory in (d).

Figure 2: Reconstructions of the homogeneous phantom for simulated data acquired under ideal conditions (top row), with the variable velocity profile seen in Figure 1 (c) (middle row), and with the deviated trajectory seen in Figure 1 (d) (bottom row). The original images are presented in (a), and (b)-(f) contain the reconstructions using: (b) dynamic sensitivity averaging, (c) GRAPPA, (d) SENSE, (e) SENSE+L1 and (f) WARF.

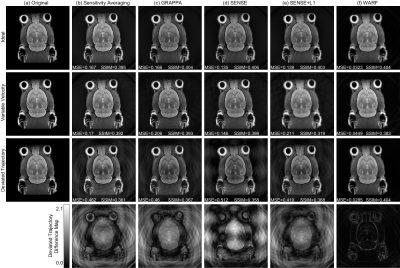
Figure 3: Reconstructions of the mouse head image for simulated data acquired under ideal conditions (top row), with the variable velocity profile seen in Figure 1 (c) (second row), and with the deviated trajectory seen in Figure 1 (d) (third row), and difference maps for the deviated trajectory reconstructions (fourth row). The original images are presented in (a), and (b)-(f) contain the reconstructions using: (b) dynamic sensitivity averaging, (c) GRAPPA, (d) SENSE, (e) SENSE+L1 and (f) WARF.

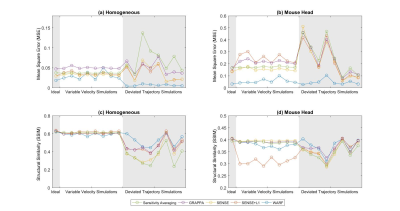
Figure 4: The Mean Square Error (top row) and Structural Similarity (bottom row) achieved using WARF and four pre-existing reconstruction methods on each of the 17 sets of simulated data with the homogeneous phantom ((a) and (c)) and the mouse head image ((b) and (d)).

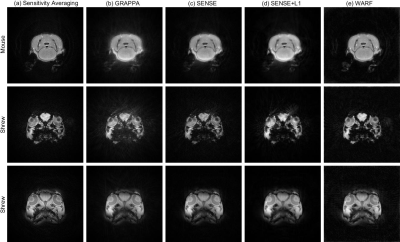
Figure 5: Reconstructions from experimental scans of a mouse (top row) and a shrew (bottom two rows) using (a) sensitivity averaging, (b) GRAPPA, (c) SENSE, (d) SENSE+L1 and (e) WARF.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
0601