0599

Deep subspace learning: Enhancing speed and scalability of deep learning-based reconstruction of dynamic imaging data

Christopher M. Sandino¹, Frank Ong¹, and Shreyas S. Vasanawala²
¹Department of Electrical Engineering, Stanford University, Stanford, CA, United States, ²Department of Radiology, Stanford University, Stanford, CA, United States

Synopsis

Unrolled neural networks (UNNs) have surpassed state-of-the-art methods for dynamic MR image reconstruction from undersampled k-space measurements. However, 3D UNNs suffer from high computational complexity and memory demands, which limit applicability to large-scale reconstruction problems. Previously, subspace learning methods have leveraged low-rank tensor models to reduce their memory footprint by reconstructing simpler spatial and temporal basis functions. Here, a deep subspace learning reconstruction (DSLR) framework is proposed to learn iterative procedures for estimating these basis functions. As proof of concept, we train DSLR to reconstruct undersampled cardiac cine data with 5X faster reconstruction time than a standard 3D UNN.

Introduction

Unrolled neural networks (UNNs) have surpassed state-of-the-art methods for recovering dynamic MR images from undersampled measurements by synergistically leveraging physics-based models and deep priors for reconstruction^1–4. In particular, many unrolled methods utilize 3D convolutional neural networks (CNNs) to learn deep spatiotemporal priors from historical dynamic imaging data. Compared to their 2D counterparts, however, 3D CNNs are computationally and memory expensive leading to relatively long reconstruction times and limited network depth. Thus, more scalable UNN architectures are necessary to apply these methods to higher-dimensional reconstruction problems^5–8.

Previously, subspace learning methods^9–12 have leveraged low-rank tensor models to not only regularize dynamic image reconstruction problems, but also reduce their memory footprint by reconstructing simpler spatial and temporal basis functions. Recently, 2D CNNs were used to learn and accelerate procedures for estimating spatial basis functions for 5D cardiac multi-tasking¹³. In this work, a deep subspace learning reconstruction (DSLR) framework is proposed to learn iterative procedures for jointly estimating both spatial and temporal basis functions for dynamic image reconstruction. As a proof of concept, we train our DSLR network to reconstruct vastly undersampled 2D cardiac cine data, and show that it can accelerate reconstruction time by a factor of 5 compared to a 3D UNN⁴ without significantly compromising image quality.

Theory

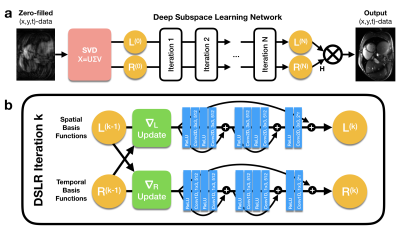
A partially separable function model⁹ is used to factorize dynamic data into a product of two matrices $$$X=LR^H$$$ (Fig. 1). $$$L$$$ and $$$R$$$ can be jointly estimated by iteratively solving the following optimization problem:$$\underset{L,R}{\text{arg min }}||Y-ALR^H||_F^2+\Psi(L)+\Phi(R)\text{ [Eq.1]}$$where $$$Y$$$ is the raw k-space data and $$$A$$$ is the sensing matrix comprised of coil sensitivity maps, Fourier transform, and k-space sampling mask. In general, this problem is ill-posed and requires regularization functions $$$\Psi$$$ and $$$\Phi$$$ to converge. An alternating minimization approach can be used to iteratively minimize the objective function in Eq. 1 by repeatedly fixing one variable and solving for the other¹⁴:$$L^{(k+1)}=\underset{L}{\text{arg min }}||Y-ALR^{(k)H}||_F^2+\Psi(L)\text{ [Eq.2]}$$$$R^{(k+1)}=\underset{R}{\text{arg min }}||Y-AL^{(k)}R^H||_F^2+\Phi(R)\text{ [Eq.3]}$$Each of these sub-problems is convex with respect to the optimization variable, and therefore, can be solved using proximal gradient descent:
$$L^{(k+1)}=\text{prox}_\Psi\big(L^{(k)}-\alpha^{(k)}A^H(Y-AL^{(k)}R^{(k)H})R^{(k)}\big)\text{ [Eq.4]}$$$$R^{(k+1)}=\text{prox}_\Phi\big(R^{(k)}-\alpha^{(k)}(Y-AL^{(k)}R^{(k)H})^HAL^{(k)}\big)\text{ [Eq.5]}$$where $$$\text{prox}_\Psi$$$ and $$$\text{prox}_\Phi$$$ are the proximal operators of $$$\Psi$$$ and $$$\Phi$$$ respectively. Previous works^10,11 have proposed hand-crafted regularization functions (i.e. temporal sparsity, nuclear norm) to solve this problem. Inspired by recent works on UNNs, we propose to implicitly learn these functions by explicitly learning their proximal operators with 2D and 1D CNNs.

Methods

Network architecture: The proposed DSLR network architecture iteratively estimates spatial and temporal basis functions by unrolling the algorithm in Eqs. 4&5 and replacing the proximal basis updates with 2D spatial and 1D temporal residual networks¹⁵ (Fig. 2). The entire network is trained end-to-end in a supervised fashion using a pixel-wise L₁-loss between the DSLR network output and fully-sampled reference images. The network is implemented in TensorFlow, and trained using the Adam optimizer¹⁶ on an NVIDIA Tesla V100 16GB graphics card.

Training data: With IRB approval, fully sampled balanced SSFP 2D cardiac cine datasets were acquired from 15 volunteers at different cardiac views and slice locations on 1.5T and 3.0T GE (Waukesha, WI) scanners using a 32-channel cardiac coil. All datasets are coil compressed¹⁷ to 8 virtual channels for speed and memory considerations. For training, 12 volunteer datasets are split slice-by-slice to create 190 unique cine slices, which are further augmented by random flipping, cropping along readout, and applying many variable-density undersampling masks (R=12). Two volunteer datasets are used for validation, and the remaining dataset for testing.

Evaluation: We compare three different reconstruction methods with respect to reconstruction speed and standard image quality metrics (PSNR,SSIM):

l₁-ESPIRiT¹⁸: Spatial and temporal total variation priors, 200 iterations (Implemented in BART¹⁹)
DL-ESPIRiT⁴: Deep 3D CNN prior, 10 iterations, 175 filters/conv
DSLR: Deep 2D/1D CNN basis priors, 16 basis functions, 10 iterations, 512 filters/conv

Networks 2&3 are trained using the same dataset described previously. All reconstructions are performed on an NVIDIA 1080 Ti 11GB graphics card.

Results

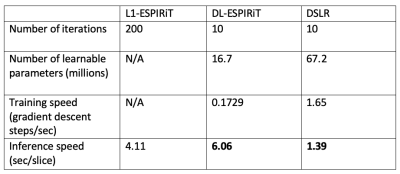
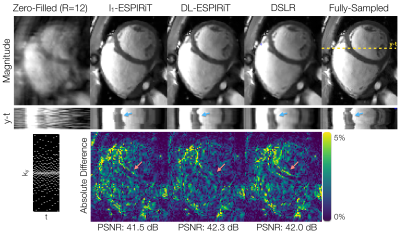
The proposed DSLR network shows 10X accelerated training speed, and 5X accelerated reconstruction time compared to the DL-ESPIRiT network (Fig. 3). DSLR and DL-ESPIRiT show comparable image quality in test reconstructions of 12X accelerated data (Fig. 4). They are also comparable with respect to PSNR; however, DL-ESPIRiT slightly outperforms DSLR with respect to SSIM (Fig. 5).

Discussion & Conclusion

The DSLR framework combines ideas from subspace learning methods and UNNs to produce a scalable and efficient technique for reconstructing high-dimensional MRI data. Due to lower memory demand, larger DSLR networks with >4X learnable parameters than DL-ESPIRiT can be trained on a single GPU. Furthermore, both training and reconstruction speeds are enhanced due to simpler 2D and 1D CNNs within the DSLR network architecture. DL-ESPIRiT and DSLR reconstructions depict similar image quality, although DSLR images are slightly blurred in localized areas with faster dynamics. Globally low-rank models⁹, such as the one used in this work, have been shown to produce temporal blurring in datasets with rapidly varying dynamics. Integrating more generalized models such as locally low-rank²⁰ for improved temporal sharpness will be the subject of future work. Furthermore, the low-rank tensor model allows the number of learnable parameters to scale linearly with data dimensionality. High-dimensional DSLR for 4D/5D cardiac imaging⁷ will also be investigated in the future.

Acknowledgements

NIH R01EB009690-05, GE Healthcare, National Science Foundation Graduate Research Fellowship

References

1. Schlemper J, Caballero J, Hajnal JV, Price A, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging. 2018;37(2):491–503. doi:10.1007/978-3-319-59050-9_51

2. Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, Rueckert D. Convolutional recurrent neural networks for dynamic MR image reconstruction. IEEE Trans Med Imaging. 2019;38(1):280–290. doi:10.1109/TMI.2018.2863670

3. Biswas S, Aggarwal HK, Jacob M. Dynamic MRI using model-based deep learning and SToRM priors: MoDL-SToRM. Magn Reson Med. 2019;82(1):485-494. doi:10.1002/mrm.27706

4. Sandino CM, Lai P, Vasanawala SS, Cheng JY. DL-ESPIRiT: Improving robustness to SENSE model errors in deep learning-based reconstruction. In: Proceedings of 27th Annual Meeting of the International Society of Magnetic Resonance in Medicine. Montreal, Quebec, Canada; 2019.

5. Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn Reson Med. 2016;75(2):775-788. doi:10.1002/mrm.25665

6. Tamir JI, Uecker M, Chen W, et al. T2 Shuffling: Sharp, Multi-Contrast, Volumetric Fast Spin-Echo Imaging. Magn Reson Med. 2017;77(1):180-195. doi:10.1002/mrm.26102

7. Cheng JY, Zhang T, Alley MT, et al. Comprehensive Multi-Dimensional MRI for the Simultaneous Assessment of Cardiopulmonary Anatomy and Physiology. Sci Rep. 2017;7(1):1-15. doi:10.1038/s41598-017-04676-8

8. Ong F, Zhu X, Cheng JY, et al. Extreme MRI: Large-Scale Volumetric Dynamic Imaging from Continuous Non-Gated Acquisitions. ArXiv:1909.13482 Phys. September 2019. http://arxiv.org/abs/1909.13482.

9. Liang ZP. Spatiotemporal imaging with partially separable functions. In: Proceedings of the 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro. ; 2007. doi:10.1109/NFSI-ICFBI.2007.4387720

10. Lingala SG, Jacob M. Blind compressive sensing dynamic MRI. IEEE Trans Med Imaging. 2013;32(6):1132–45. doi:10.1109/TMI.2013.2255133

11. Mardani M, Mateos G, Giannakis GB. Subspace Learning and Imputation for Streaming Big Data Matrices and Tensors. IEEE Trans Signal Process. 2015;63(10):2663-2677. doi:10.1109/TSP.2015.2417491

12. Christodoulou AG, Shaw JL, Nguyen C, et al. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nat Biomed Eng. 2018;2(4):215-226. doi:10.1038/s41551-018-0217-y

13. Chen Y, Shaw JL, Xie Y, Li D, Christodoulou AG. Deep Learning Within a Priori Temporal Feature Spaces for Large-Scale Dynamic MR Image Reconstruction: Application to 5-D Cardiac MR Multitasking. Medical Image Computing and Computer Assisted Intervention – MICCAI 2019. Lecture Notes in Computer Science. Cham: Springer International Publishing; 2019:495-504. doi:10.1007/978-3-030-32245-8_55

14. Udell M, Horn C, Zadeh R, Boyd S. Generalized Low Rank Models. Found Trends® Mach Learn. 2016;9(1):1-118. doi:10.1561/2200000055

15. He K, Zhang X, Ren S, Sun J. Deep Residual Learning for Image Recognition. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR). ; 2016. doi:10.1109/CVPR.2016.90

16. Kingma DP, Ba JL. Adam: A method for stochastic gradient descent. In: Proceedings of the 3rd International Conference on Learning Representations. San Diego, CA, United States; 2015.

17. Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn Reson Med. 2013;69(2):571-582. doi:10.1002/mrm.24267

18. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT - An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990–1001. doi:10.1002/mrm.24751

19. Uecker M, Ong F, Tamir JI, et al. Berkeley advanced reconstruction toolbox. In: Proceedings of 23rd Annual Meeting of the International Society of Magnetic Resonance in Medicine. Toronto, Ontario, Canada; 2015.

20. Trzasko JD, Manduca A. Local versus global low-rank promotion in dynamic MRI series reconstruction. In: Proceedings of the 19th Annual Meeting of the International Society of Magnetic Resonance in Medicine. Montreal, Quebec, Canada; 2011.

Figures

Figure 1: Low-rank tensor factorization of cardiac cine data (animated GIF). A dynamic dataset $$$X$$$ is decomposed into a product of two matrices $$$L\in\mathbb{C}^{mn\times r}$$$ and $$$R\in\mathbb{C}^{t\times r}$$$ comprised of r spatial r and temporal basis functions respectively. We propose a novel UNN architecture to directly estimate the compressed representations L and R using simpler 2D and 1D networks. Images above show the magnitude of complex-valued basis functions derived using the proposed DSLR algorithm. Only a subset of the total 16 basis functions are shown.

Figure 2: DSLR network architecture. (a) A zero-filled reconstruction is decomposed using the singular value decomposition (SVD) to initialize the basis vectors as $$$L^{(0)}=U\Sigma^{1/2}$$$ and $$$R^{(0)}=V\Sigma^{1/2}$$$ where $$$U$$$ and $$$V$$$ are the truncated left and right singular vectors respectively. (b) $$$L$$$ and $$$R$$$ are iteratively updated by gradient updates (green) and residual CNNs (blue). Prior to each CNN update, each complex-valued basis function is separated into real and imaginary components and stacked along the feature dimension.

Figure 3: Table comparing computational complexity between l₁-ESPIRiT, DL-ESPIRiT, and DSLR networks. Inference speed benchmarks were obtained by averaging reconstruction times of 10 slices with 224x168 matrix size, 8 virtual coils, and 20 cardiac phases on an NVIDIA GTX 1080 Ti. DL-ESPIRiT reconstruction times were slightly slower than L1-ESPIRiT, while DSLR reconstruction times were faster than both other methods.

Figure 4: Reconstruction comparison. A fully-sampled, short-axis view acquired on a 1.5T scanner is retrospectively undersampled by a factor of 12, and reconstructed with l₁-ESPIRiT, DL-ESPIRiT, DSLR algorithms. Both DL-ESPIRiT and DSLR reconstructions show realistic cardiac motion and good agreement with fully-sampled images. Slight temporal blurring is apparent in the DSLR images along the septum, which is evident in the y-t profile (blue arrows), and absolute differences images (red arrows).

Figure 5: Image quality metrics. Peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) are shown for each of the ten test slices. Both DL-ESPIRiT and DSLR networks consistently outperform l₁-ESPIRiT with respect to both PSNR and SSIM. DSLR outperforms DL-ESPIRiT for certain slices with respect to PSNR. However, DL-ESPIRiT slightly outperforms DSLR for all slices with respect to SSIM. Because it attempts to capture changes in structural information through 2D space and time, SSIM may be more sensitive to temporal blurring in the DSLR images compared to PSNR.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

0599