0598
Real-time 3D respiratory motion estimation for MR-guided radiotherapy using low-rank MR-MOTUS1Computational Imaging Group for MR diagnostics and Therapy, Center for Image Sciences, University Medical Center Utrecht, Utrecht, Netherlands, 2Department of Radiology, Division of Imaging and Oncology, University Medical Center Utrecht, Utrecht, Netherlands
Synopsis
We propose low-rank MR-MOTUS, a framework for real-time reconstructions of 3D respiratory motion-fields for MR-guided radiotherapy. Low-rank MR-MOTUS factorizes space-time motion-fields into static spatial components and dynamic temporal components. This allows to 1) exploit spatial and temporal correlations in motion, and 2) split the reconstruction into a large-scale off-line training phase, and a small-scale on-line inference phase. Results show that in the on-line inference phase 3D respiratory motion can be estimated in 130ms, from data acquired in 24ms. This yields a total latency of 154ms, and low-rank MR-MOTUS thereby paves the way for real-time MR-guided radiotherapy on the MR-linac.
Introduction
The MR-linac[1], a combination of an MRI-scanner and linear accelerator, can enable real-time MR-guided radiotherapy (MRgRT) when given a continuous stream of high-quality and low-latency tumor motion estimates[2]. Focusing on the latter, we previously introduced MR-MOTUS[3]: a $$$k$$$-space domain framework which provides high-quality motion-fields with high temporal resolution (>10Hz)[4]. However, MR-MOTUS has relatively long reconstruction times ($$$\sim$$$minutes) and is therefore unable to meet the low-latency requirement for real-time MRgRT.In this work we propose low-rank MR-MOTUS, which does meet the low-latency requirement. Low-rank MR-MOTUS factorizes space-time motion-fields into fixed spatial components and dynamic temporal components. This allows to 1) exploit spatial and temporal correlations in motion, and 2) split the reconstruction into a large-scale off-line training phase, and a small-scale on-line inference phase. In the on-line phase the temporal components are estimated with a latency of 155ms, thereby paving the way for real-time MRgRT on the MR-linac.
Theory
MR-MOTUSThe MR-MOTUS forward model[3] explicitly relates dynamic motion-fields $$$\mathbf{T}_t\in\mathbb{R}^{3N}$$$ and a reference image $$$\mathbf{q}_0\in\mathbb{C}^N$$$ to the dynamic $$$k$$$-space measurements $$$s_t$$$: $$s_t[\mathbf{k}]=F(\mathbf{T}_t|\mathbf{q}_0)[\mathbf{k}]=\int_\Omega q_0(\mathbf{r}_0)e^{-i2\pi\mathbf{k}\cdot\mathbf{T}_t(\mathbf{r}_0)}\ \text{d}\mathbf{r}_0.\quad\quad\quad(1)$$Space-time motion-fields can be reconstructed from minimal $$$k$$$-space snapshots $$$s_t$$$ by solving the inverse problem while exploiting the correlations of motion in both space and time, with appropriate regularization $$$\mathcal{R}$$$:$$\min_{\mathbf{T}} \ \frac{1}{M}\sum_{t=1}^M \left\lVert \mathbf{F}( \mathbf{T}_t ) - \mathbf{s}_t \right\rVert_2^2 + \lambda \mathcal{R}(\mathbf{T}).\quad\quad\quad(2)$$However, the number of parameters and reconstruction time of (2) scale with the required number of dynamics $$$M$$$ (~102). Consequently, the reconstruction times are in the order of minutes which limits the applicability to low-latency processes such as real-time MRgRT.
Low-rank MR-MOTUS
We propose to factorize $$$\mathbf{T}_t$$$ in spatial ($$$\mathbf{\Phi}$$$) and temporal components ($$$\mathbf{\Psi}$$$):$$\mathbf{T}_t(\mathbf{r})=\sum_{q=1}^R \mathbf{\Phi}^q(\mathbf{r})\Psi^q(t).\quad\quad\quad(3)$$Here $$$\mathbf{\Phi}^q$$$ denote the voxel-by-voxel principal direction and magnitude, and $$$\Psi^q$$$ denote the temporal scaling (see Fig. 2a). Mathematically, (3) can be interpreted as the explicit constraint $$$\textrm{rank}(\mathbf{T})\le R$$$, which has appeared previously for image reconstruction[5]. The factorization naturally leads to two phases in the motion-field reconstruction: 1) an off-line training phase which solves Equation (2) with $$$\textrm{rank}(\mathbf{T})\le R$$$, and 2) an on-line inference phase which reconstructs the time-dependent factor $$$\mathbf{\Psi}_t$$$:
Off-line training:
$$\mathbf{\Phi}^*,\mathbf{\Psi}^*=\text{argmin}_{\mathbf{\Phi},\mathbf{\Psi}}\quad\frac{1}{M_\text{train}}\sum_{t=1}^{M_{\text{train}}} \left\lVert \mathbf{F}\left( \mathbf{\Phi}\mathbf{\Psi}^T_t \right) - \mathbf{s}_t \right\rVert_2^2 + \lambda \mathcal{R}(\mathbf{\Phi},\mathbf{\Psi}).\quad\quad\quad(4)$$
On-line inference:
$${\mathbf{\Psi}_t} = \text{argmin}_{\mathbf{\Psi}_t}\label{eq:onlineinference} \ \left\lVert \mathbf{F}\left( \mathbf{\Phi}^*\mathbf{\Psi}^T_t \right) - \mathbf{s}_t \right\rVert_2^2, \qquad t>M_\text{train}.\quad\quad\quad(5)$$
In addition to the explicity low-rank constraint, (4) was regularized by enforcing orthonormal and orthogonal columns in $$$\mathbf{\Phi}$$$ and $$$\mathbf{\Psi}$$$, respectively. Here $$$\mathbf{\Psi}_t\in\mathbb{R}^R$$$, where typically $$$R\le3$$$ suffices. Hence, (5) is very small-scale and can be solved in under 130ms for $$$R=1$$$.
Methods
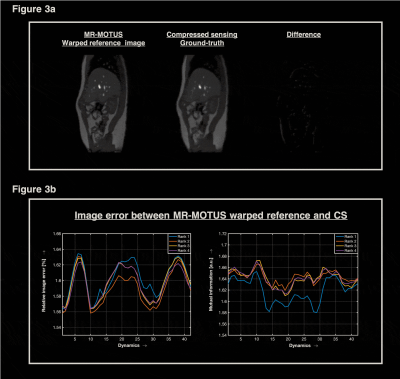
Low-rank motion analysis on 2D dataTwo-dimensional $$$k$$$-space data were acquired in a single volunteer using a continuous 2D sagittal golden-angle radial readout and a spoiled gradient echo sequence. The volunteer was instructed to start with 10 second breath-hold and then continue breathing. From the breath-hold data we reconstructed a reference image $$$\vec{q}_0$$$ and motion-fields were reconstructed off-line from all free-breathing data using 5 spokes/dynamic. The motion-field reconstructions were performed with different ranks ($$$R=1,\dots,4)$$$ and compared with ground-truth images reconstructed with 25 spokes/dynamic using compressed sensing[6].
Real-time 3D respiratory motion-field reconstructions
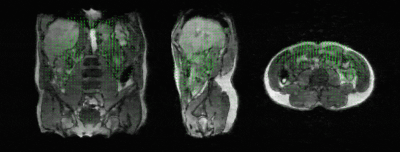
3D respiratory motion-fields were reconstructed from prospectively undersampled non-Cartesian $$$k$$$-space data with a rank-1 motion model. Data was continuously acquired during breath-hold and free-breathing using a spoiled gradient echo with a 3D golden mean cone trajectory[7]. From $$$\sim$$$30s breath-hold a reference image was reconstructed. First, the off-line large-scale problem (4) was solved using 96 dynamics and 40 cones/dynamic. Subsequently, the on-line small-scale problem (5) was solved in 130ms/dynamic, using a total of only 6 $$$k$$$-space points/dynamic extracted from 3 different cones. See Fig. 2b for a complete overview of the low-rank reconstructions.
Results
The low-rank analysis for $$$R=1,\dots,4$$$ is shown in Fig. 3. All reconstructions show good correspondence to the ground-truth compressed sensing reconstruction and minimal differences can be observed between the different ranks.Fig. 4 shows 3D rank-1 respiratory motion-fields that were reconstructed in 130ms/dynamic in the on-line training phase, from data acquired in 24ms/dynamic. The temporal resolution was decreased for visualization purposes.
Discussion & Conclusion
We have enhanced MR-MOTUS with an explicit low-rank representation to reconstruct time-dependent motion-fields. Results confirm the validity of the low-rank representation. Reconstructions in the on-line phase show promising results with reconstruction times of about 130ms/dynamic. The required data was acquired in just 24ms/dynamic, yielding a total reconstruction latency of 154ms.In practice we envision the following workflow. A reference image could be obtained with a respiratory-sorted 3D golden-mean-cone acquisition of 2-3 minutes. This same data can be used to train the low-rank model. Finally, motion-fields can be inferred from continuously acquired data during free-breathing with a latency of 154ms and a temporal resolution of 40Hz. Thus, low-rank MR-MOTUS can thereby open the window for real-time MRgRT on the MR-linac.
Acknowledgements
This research is funded by the Netherlands Organisation for Scientific Research, domain Applied and Engineering Sciences, Grant number 15115.References
- Raaymakers, B., Lagendijk, J., Overweg, J., Kok, J., Raaijmakers, A., Kerkhof,E., Van der Put, R., Meijsing, I., Crijns, S., Benedosso, F., et al. Integrating a 1.5T MRI scanner with a 6 MV accelerator: proof of concept. Physics in Medicine & Biology 54,12, 2009.
- Glitzner, M., Woodhead, P. L., Borman, P. T., Lagendijk, J. J., and Raaymakers,B. W. MLC-tracking performance on the Elekta unity MRI-linac. Physics in Medicine & Biology, 2019.
- Huttinga, N.R.F., van den Berg, C.A.T., Luijten, P.R., and Sbrizzi, A. MR-MOTUS: Model-based non-rigid motion estimation for MR-guided radiotherapy using a reference image and minimal k-space data. Physics in Medicine & Biology (in press), 2019.
- Huttinga, N.R.F., Bruijnen, T., van den Berg, C.A.T., Luijten, P.R. and Sbrizzi, A. Prospective 3D+t non-rigid motion estimation at high frame-rate from highly undersampled k-space data: validation and preliminary in-vivo results, Proceedings 27th annual meeting ISMRM, Montréal, Canada, 2019.
- Ong, F., Zhu, X., Cheng, J. Y., Johnson, K. M., Larson, P. E., Vasanawala, S. S., & Lustig, M. Extreme MRI: Large-Scale Volumetric Dynamic Imaging from Continuous Non-Gated Acquisitions. arXiv preprint arXiv:1909.13482, 2019.
- Uecker, M., Ong, F., Tamir, J. I., Bahri, D., Virtue, P., Cheng, J. Y., Zhang, T.,and Lustig, M. Berkeley advanced reconstruction toolbox. Proc. Intl. Soc. Mag. Reson.Med 2015, vol. 23, p. 2486.
- Johnson, K. M. Hybrid radial-cones trajectory for accelerated MRI. Magnetic resonance in medicine 77, 3,1068–1081, 2017.
Figures
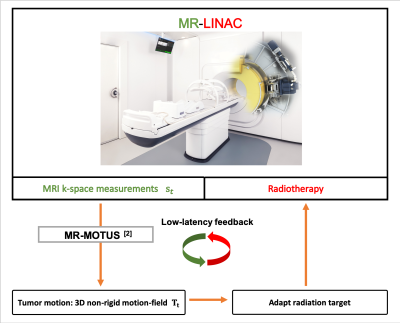
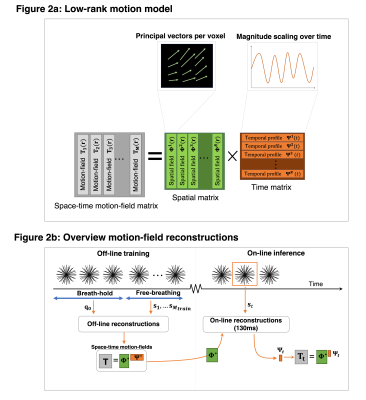
Figure 2a: Illustration of the low-rank motion model. Time-dependent motion-fields are factorized in static spatial components and dynamic temporal components.
Figure 2b: Overview of low-rank reconstructions. First, a reference image is reconstructed from breath-hold data. Next, in the off-line training phase both spatial and temporal components of the motion model are reconstructed. Finally, in the on-line inference phase the trained spatial components are fixed and only temporal components are reconstructed.