0596

3D-BUDA Enables Rapid Distortion-Free QSM Acquisition

Berkin Bilgic¹, Benedikt A Poser², Christian Langkammer³, Kawin Setsompop¹, and Congyu Liao¹
¹Martinos Center for Biomedical Imaging, Charlestown, MA, United States, ²Maastricht University, Maastricht, Netherlands, ³Department of Neurology, Medical University of Graz, Graz, Austria

Synopsis

We introduce 3D blip-up and -down acquisition (3D-BUDA) for 3D echo planar imaging (3D-EPI). We acquire two-shots of 3D-EPI with alternating phase-encoding to estimate B₀ information. Incorporating this into the joint reconstruction of the shots eliminates distortion and enables signal averaging, permitting a 22-second, high-SNR acquisition at 1 mm³ resolution. While shifted sampling between the shots provides complementary k-space coverage, using low-rank regularization eliminates shot-to-shot variations. SNR gain of 7T allows for additional partition acceleration, enabling a 9-second whole-brain scan at R_inplane×R_z=5×2. These are combined with a self-supervised dipole inversion algorithm for Quantitative Susceptibility Mapping (QSM) which outperforms state-of-the-art reconstructions.

Introduction

3D-Gradient Echo (GRE) is the workhorse sequence for susceptibility imaging. As the optimal phase contrast-to-noise ratio (CNR) is achieved at late echo times (TE=T₂*)(1), the repetition time (TR) is routinely pushed beyond 35–40 msec at high field. A fully sampled, whole-brain acquisition at 1 mm³ resolution will thus necessitate ~20 min of scan time. Controlled aliasing can employ acceleration rates of up to R_y×R_z = 3×3-fold, thus lowering the scan time to 2–3 min (2,3).
Going faster is possible through 3D-EPI (4,5), which can provide whole-brain coverage at 1 mm isotopic resolution in 10 seconds (6), but comes at the cost of geometric distortion and requires a couple of averages to boost SNR. While ultra-high field may obviate the need for averaging, distortion is further aggravated and can only be partially mitigated using high R_inplane.
We introduce 3D-BUDA to eliminate distortion in 3D-EPI. We jointly reconstruct two shots made with alternating phase-encoding polarities and incorporate B₀ information into the parallel imaging model. Shifting the k-space pattern of the shots enables high R_inplane without noise amplification. Joint reconstruction averages the shots in k-space, eliminating the need for additional signal averaging. We exploit the SNR benefit of 7T to enable partition acceleration, so that 1 mm³ QSM acquisition becomes possible in 9 seconds at R_inplane×R_z = 5×2. We finally propose BM4D-QSM, a self-supervised dipole inversion algorithm, to accompany this efficient acquisition.

3D-BUDA Acquisition and Reconstruction

Fig1 shows 3D-BUDA acquisition, where two 3D-EPI volumes are collected with blip-up and -down polarity with a ∆k_y shift. Each volume is reconstructed using SENSE (7), where pile-ups and stretching are visible (yellow and blue arrows). FSL topup (8,9) uses these volumes to estimate a field map, which is incorporated in the 3D-BUDA joint reconstruction:
$$min_{\bf x} \sum_{t=1}^2 \parallel F_t E C x_t - d_t \parallel _2^2 +\lambda\parallel \mathcal{H}(\bf x)\parallel_*$$
where $$$F_t$$$ is the undersampled Fourier operator in $$$t$$$^th shot, $$$E$$$ is the field map, and $$$C$$$ are the ESPIRiT sensitivities estimated from a 2-second FLASH prescan (included in the reported scan times). $$$x_t$$$ is the distortion-free image and $$$d_t$$$ are the k-space data for shot $$$t$$$. The constraint $$$\parallel \mathcal{H}(\bf x)\parallel_*$$$ enforces low-rank prior on the block-Hankel representation of the two-shot data $$$\bf x$$$, which is applied in k-space using 11x11 blocks.

Data Acquisition at 3T

3D-BUDA were acquired using R_inplane=4 with ∆k_y=2 shift. Matrix size was 224×224×144 at 1 mm³ resolution using TE/TR=36/72 msec with selective excitation at the Ernst angle on a Siemens Trio equipped with a 32-chan head coil. Fat signal was mitigated using water selective excitation to reduce the TR.

Fig2a shows SENSE reconstructions, each of which took 10 seconds to acquire (+2 second prescan). The 22-second 3D-BUDA was able to eliminate distortion and improve SNR.

Data Acquisition at 7T

To mitigate the increased distortion at 7T (Siemens Magnetom), R_inplane was increased to 5 with ∆k_y=3 shift. This permitted TE/TR=25/50 msec, thus reducing the acquisition time to 9 seconds (7+2) per volume.
Fig2b: Strong physiologic variations and distortion affected SENSE reconstructions. 16-second 3D-BUDA eliminated the distortion and improved the SNR.
Fig3a: Compares hybrid-SENSE (10) (jointly reconstruct the blip-up/down shots without low-rank constraint) and 3D-BUDA. Hankel regularization mitigated artifacts (yellow arrows) and improved SNR.
Fig3b: R_inplane×R_z=5×2 acceleration brought the total scan time to 9 seconds, where 3D-BUDA continued to provide noise and artifact mitigation compared to hybrid-SENSE.

BM4D-QSM: Self-supervised Dipole Inversion

We propose to learn a tailored regularizer for dipole inversion from the susceptibility map itself using BM4D block-matching (11) with a decoupled algorithm where the following updates are applied iteratively (12):

$$\hat\chi_i=argmin_{\chi}\parallel F^{-1}DF\chi -\phi \parallel_2^2+\alpha\parallel \chi-\chi_{i-1} \parallel_2^2$$
$$\chi_i=argmin_{\chi}\parallel \chi -\hat\chi_i \parallel_2^2+\beta\parallel \Psi_i\chi \parallel_1$$
where $$$D$$$ is the dipole kernel, $$$F$$$ is a 3D-DFT operator, $$$\phi$$$ is the tissue phase and $$$\hat \chi_i$$$ is an interim map in iteration $$$i$$$. This is used for creating an adaptive sparse transform $$$\Psi_i$$$, which is used in soft-thresholding to yield $$$\chi_i$$$.

We validated BM4D-QSM on the QSMnet dataset (13) against a 5-direction COSMOS (14) based on GRE data at 1 mm³ resolution. Fig4 shows that BM4D outperformed the state-of-the-art FANSI (15), and eliminated streaking artifacts without oversmoothing. All methods were optimized for best RMSE. BM4D used $$$\alpha$$$=0.1 and $$$\beta$$$ was reduced from 1 to 0.002 over 5 iterations.

Rapid BM4D-QSM Acquisition using 3D-BUDA

The same BM4D parameters were applied on the 3D-BUDA data in Fig5. Phase was processed using Laplacian unwrapping (16) and V-SHARP (17,18).

Discussion

We presented 3D-BUDA for rapid and distortion-free acquisition and combined it with a new dipole inversion algorithm for high-quality QSM. Rather than collecting multiple averages of 3D-EPI with the same polarity to increase SNR, BUDA averages two-shots with inverted polarity in k-space with the aid of a B₀ map. This simultaneously mitigates g-factor penalty and eliminates distortion.
Going to 7T allows for partition acceleration as the intrinsic $$$\sqrt{R_z}$$$ SNR loss is accounted for by the signal boost. This permitted 1 mm³ whole-brain acquisition in 9 seconds. However, increased physiologic variations adversely affected image quality. While BUDA mitigated these and eliminated distortion, it is unable to address the worsened intravoxel dephasing. Increased field inhomogeneity also affected the QSM quality (last two rows of Fig5). To help address this, rapid 3D-BUDA could largely facilitate multi-head orientation acquisition to further improve the conditioning of dipole inversion.

Acknowledgements

This work was supported by:

NIBIB Award Number: P41 EB015896, R01 EB017337, R01 EB019437, R01 EB020613 and U01 EB025162;

NIMH, Award Number: R01 MH116173 and R24 MH106096;

Shared instrumentation grants S10-RR023401 and S10- RR023043; and

NVIDIA GPU grants.

References

1. Wu B, Li W, Avram AV, Gho S-M, Liu C. Fast and tissue-optimized mapping of magnetic susceptibility and T2* with multi-echo and multi-shot spirals. Neuroimage 2012;59:297–305 doi: 10.1016/j.neuroimage.2011.07.019.

2. Breuer FA, Blaimer M, Mueller MF, et al. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA). Magn. Reson. Med. 2006;55:549–556 doi: 10.1002/mrm.20787.

3. Bilgic B, Gagoski BA, Cauley SF, et al. Wave-CAIPI for highly accelerated 3D imaging. Magn. Reson. Med. 2015;73:2152–2162 doi: 10.1002/mrm.25347.

4. Poser BA, Koopmans PJ, Witzel T, Wald LL, Barth M. Three dimensional echo-planar imaging at 7 Tesla. Neuroimage 2010;51:261–266 doi: 10.1016/j.neuroimage.2010.01.108.

5. Zahneisen B, Ernst T, Poser BA. SENSE and simultaneous multislice imaging. Magn. Reson. Med. 2015;74:1356–1362 doi: 10.1002/mrm.25519.

6. Langkammer C, Bredies K, Poser BA, et al. Fast quantitative susceptibility mapping using 3D EPI and total generalized variation. Neuroimage 2015;111 doi: 10.1016/j.neuroimage.2015.02.041.

7. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 1999;42:952–962.

8. Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 2003;20:870–888 doi: 10.1016/S1053-8119(03)00336-7.

9. Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004;23:S208–S219 doi: 10.1016/j.neuroimage.2004.07.051.

10. Zahneisen B, Aksoy M, Maclaren J, Wuerslin C, Bammer R. Extended hybrid-space SENSE for EPI: Off-resonance and eddy current corrected joint interleaved blip-up/down reconstruction. Neuroimage 2017;153:97–108 doi: 10.1016/J.NEUROIMAGE.2017.03.052.

11. Maggioni M, Katkovnik V, Egiazarian K, Foi A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 2013;22:119–133 doi: 10.1109/TIP.2012.2210725.

12. Eksioglu EM. Decoupled Algorithm for MRI Reconstruction Using Nonlocal Block Matching Model: BM3D-MRI. J. Math. Imaging Vis. 2016;56:430–440 doi: 10.1007/s10851-016-0647-7.

13. Yoon J, Gong E, Chatnuntawech I, et al. Quantitative susceptibility mapping using deep neural network: QSMnet. Neuroimage 2018;179:199–206 doi: 10.1016/J.NEUROIMAGE.2018.06.030.

14. Liu T, Spincemaille P, de Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): A method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn. Reson. Med. 2009;61:196–204 doi: 10.1002/mrm.21828.

15. Milovic C, Bilgic B, Zhao B, Acosta-Cabronero J, Tejos C. Fast nonlinear susceptibility inversion with variational regularization. Magn. Reson. Med. 2018;80:814–821 doi: 10.1002/mrm.27073.

16. Li W, Wu B, Liu C. Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition. Neuroimage 2011;55:1645–1656 doi: 10.1016/j.neuroimage.2010.11.088.

17. Wu B, Li W, Guidon A, Liu C. Whole brain susceptibility mapping using compressed sensing. Magn. Reson. Med. 2012;67:137–147 doi: 10.1002/mrm.23000.

18. Schweser F, Sommer K, Deistung A, Reichenbach JR. Quantitative susceptibility mapping for investigating subtle susceptibility variations in the human brain. Neuroimage 2012;62:2083–100 doi: 10.1016/j.neuroimage.2012.05.067.

Figures

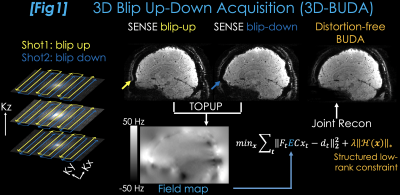
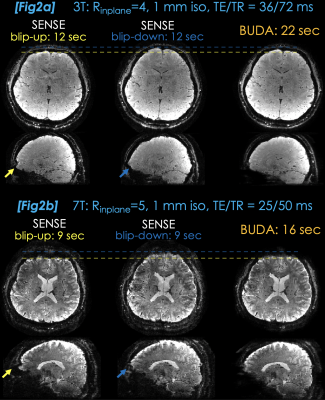
Fig1. 3D-BUDA acquires two shots of 3D-EPI data with opposite phase encoding directions using a $$$\Delta$$$k_y k-space shift between the shots. The individual shots are reconstructed using SENSE, which allows us to obtain a field map estimate using FSL's topup. This is then incorporated into the 3D-BUDA reconstruction where the two-shots are jointly reconstructed with Hankel low-rank regularization to provide distortion-free, high-SNR data.

Fig2a. SENSE reconstructions at R_inplane=4 suffer from distortion (yellow & blue arrows). These acquisitions take 12 sec (2 sec FLASH prescan included) at 1 mm³ resolution. 3D-BUDA reconstruction from a 22-sec total scan improves SNR and eliminates distortion.

Fig2b. Distortion, intravoxel dephasing and physiologic phase variations are more severe in the SENSE reconstructions at 7T. R_inplane=5 helps mitigate the distortion and reduces TR, so that each scan is completed in 9 sec. 3D-BUDA eliminates distortion and improves image quality using two-shots from a 16 sec scan.

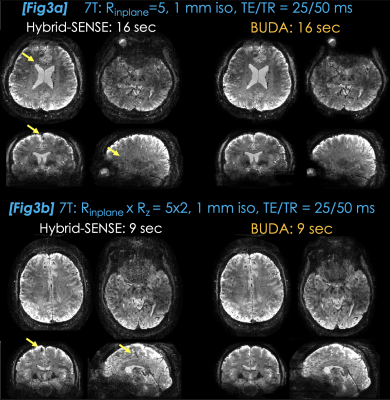
Fig3a. Hybrid-SENSE uses field map information in the parallel imaging forward model to eliminate distortion. It requires an explicit shot-to-shot phase variation estimate and suffers from reconstruction artifacts (arrows). 3D-BUDA obviates the need for phase navigation, improves SNR and better mitigates artifacts.

Fig3b. Intrinsic SNR at 7T allowed for further reducing the scan time using R_z=2 acceleration. This allowed 3D-BUDA to provide distortion-free, 1 mm isotropic GRE data from a 9 sec scan, with improved image quality over hybrid-SENSE.

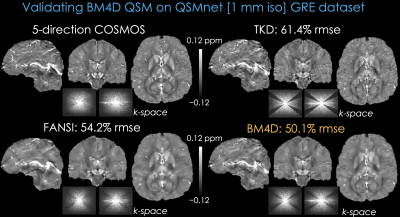
Fig4. We employed the QSMnet dataset with 5-direction COSMOS data at 1 mm isotropic resolution to validate the proposed BM4D-QSM reconstruction. Compared to the TKD benchmark and state-of-the-art FANSI algorithm, BM4D was able to improve RMSE and mitigate streaking without oversmoothing artifacts.

Fig5. Applying BM4D-QSM on the 3D-BUDA data yielded the susceptibility maps on the left, where the top row corresponds to the 22-second 3T acquisition. Middle and bottom rows depict QSM results from the 16- and 9-second 7T acquisitions, where the residual field inhomogeneity led to some artifacts.

Tissue phase data are depicted on the right, which were obtained using Laplacian unwrapping and V-SHARP filtering (25 mm largest kernel size). Despite high-SNR, some residual background field was visible in the 7T results.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

0596