Introduction

Conventional autocalibrating parallel imaging methods require autocalibrating signals (ACS) for coil sensitivity estimation¹. However, acquiring sufficient ACS data in spiral MRI prolongs the acquisition window, which can lead to blurring and artifacts due to off-resonance effect.
On the other hand, typical clinical scans collect multiple 2D slices to provide a volume coverage. The coil sensitivity varies smoothly within the image planes and along slice direction, and adjacent slices have similar coil sensitivity maps. With adjacent slices having interleaved sampling pattern, the ACS data can be obtained by combining central k-space lines from multiple adjacent slices². The adjacent slices also have similar image content due to the slow spatial variations of the subject, especially when the slice thickness/gap is sufficiently small³. These information can be incorporated into calibrationless parallel imaging reconstruction by extending the existing low rank matrix completion approaches^4-6 with tensorial expressions⁷.
In this study, we proposed to simultaneously reconstruct multiple adjacent slices through a block-wise Hankel tensor completion framework (MS-HTC) for spiral MRI, where the spiral data were undersampled using complementary sampling patterns across difference slices. The proposed approach can inherently exploit the coil sensitivity, spatial support, and image content similarities, and provide better performance over single-slice reconstruction with simultaneous autocalibrating and k-space estimation (SAKE)⁴.

Method

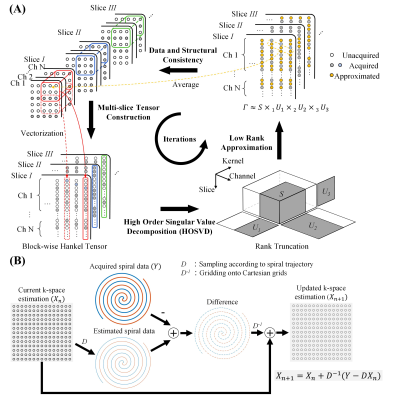
The proposed calibrationless reconstruction using low rank tensor completion consists of the following steps (Figure 1). First, multi-channel k-space data from each slice were structured into a block-wise Hankel matrix, and then stacked along a third dimension, forming a 3-order tensor, termed as multi-slice tensor in this study. As revealed in autocalibrating parallel imaging reconstruction, each k-space sample can be linearly fitted from its neighborhood within a compact kernel, and such linear dependency should be consistent across the whole k-space¹. This implies that a block-wise Hankel matrix should be inherently low-rank⁴. Due to aforementioned similarities across adjacent slices, the multi-slice tensor should be even more rank-deficient compared to the Hankel matrix constructed from a single slice. Therefore, the multi-slice tensor can be decomposed using high-order SVD (HOSVD) and approximated with rank truncation. Last, the k-space was recovered from the approximated tensor, with data and structural consistency promoted. Specifically, the multi-slice tensor elements corresponding to the same k-space sample were averaged and used as k-space estimation (structural consistency). After that, the k-space data on spiral trajectories were calculated using non-uniform FFT (NUFFT)⁸, and subtracted from the acquired spiral data. The difference was then mapped onto Cartesian grids using inverse NUFFT, and added to the current k-space estimation. This procedure minimizes the difference between estimated k-space and acquired spiral data (data consistency). Note that with such strategy, acquisition imperfections which can cause mismatch within each slice can also be compensated before NUFFT operation by considering the motion induced effect, such as phase difference in multi-shot diffusion imaging or bulk motion. These steps were repeated to update the k-space estimation iteratively until convergence.


Human brain data were acquired on a 3T Philips scanner equipped with an 8-channel head coil using a multi-slice 8-shot spin-echo (SE) regular spiral sequence, with acquisition window=21ms, TR/TE=2700/54ms, FOV=220×220mm², slice thickness/gap=4/1mm, matrix size=220×220, and SPIR (spectral pre-saturation with inversion recovery) used for fat suppression. Undersampling (R=2, 4) was performed by discarding the spiral shots in an interleaved way. The multi-slice nature of 2D acquisition allows different slices having complementary sampling pattern. In this case, the sampling for different slices complements each other by choosing the spiral shots with different rotation angles. The proposed method was compared to SAKE reconstruction, which was independently applied for single-slice data. The iteration process stopped when the update of k-space data estimation was lower than 0.1‰.

Results

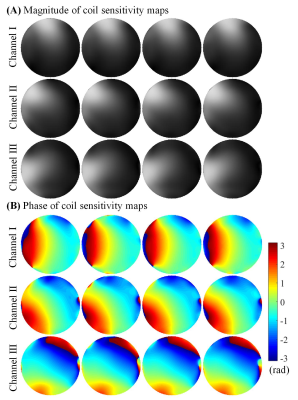
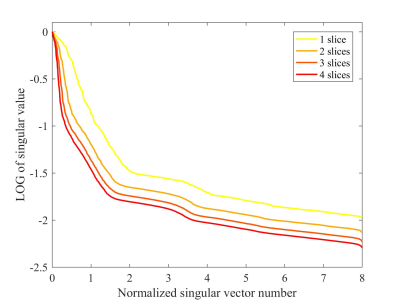
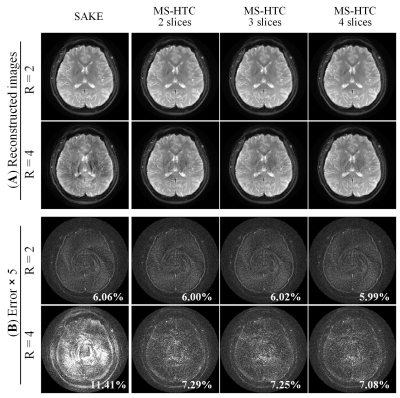
Figure 2 compares the 4 adjacent slices from MS-HTC and SAKE reconstruction at R=4. These slices have similar coil sensitivity maps in terms of their magnitude and phase (Figure 3). Fully sampled and four-fold undersampled data were also directly reconstructed using NUFFT. Direct reconstruction from four-fold undersampled data suffers from severe aliasing artifacts, which cannot be fully suppressed with SAKE. With 4 slices reconstructed together using MS-HTC, these artifacts can be significantly eliminated.
With increased number of slices being reconstructed together, the constructed tensor is more rank-deficient (Figure 4), which can lead to improved reconstruction performance, especially at high accelerations. As shown in Figure 5, at R=2, MS-HTC does not have major advantage over SAKE. However, at R=4, MS-HTC results have significantly reduced residual artifacts, and 4-slice reconstruction can provide better performance over 2-slice/3-slice reconstruction.

Discussion and Conclusions

The proposed approach outperforms existing single-slice spiral MRI reconstruction. This is achieved for the following reasons. First, spiral trajectory creates a pseudo 2D random sampling, and selecting spiral shots with different rotation angles for adjacent slices can provide complementary information. Second, the MS-HTC exploits the similar coil sensitivity, spatial support, and image content across adjacent slices through a low rank tensor completion framework. The results show that increasing the slice number can reduce the residual error. Note that the similarities among selected slices will reduce with larger slice gap or increased slice number, and the decreased similarities may undermine the performance of MS-HTC. Optimal number of slices to be reconstructed together will be studied in the future.

Acknowledgements

This study is supported in part by Hong Kong Research Grant Council (C7048-16G and HKU17115116 to E.X.W.), Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001) and Guangdong Key Technologies for Alzheimer's Disease Diagnosis and Treatment (2018B030336001) to E.X.W.