Introduction

Group-wise spatial normalization of fiber orientation distribution functions (fODF) ¹ is an important step in studies involving fixel-based analysis (FBA). ² Registration methods that aim to spatially match fODFs have been developed but have not been compared to the previous, thoroughly characterized standard, namely diffusion tensor-based registration. ^3-5 The aim of this work was to compare the accuracy in matching fODFs using fODF-based and tensor-based transformations. To also evaluate the robustness of the two registration approaches, the analysis was conducted not only using diffusion data with high angular resolution (more optimal for fODF reconstruction) but also using data with low angular resolution (less optimal for fODF reconstruction; more appropriate for tensor reconstruction). Finally, the spatial transformations derived from the two registration methods were applied to corresponding structural images to evaluate how fODF matching translated into structural matching. This project was conducted using data from older adults, as it is part of a larger effort to evaluate FBA in studies of aging.

Methods

Data
Two datasets, one with high and one with low angular resolution, were used in this work. Dataset 1 contained high angular resolution data from 24 non-demented participants of the Alzheimer’s Disease Neuroimaging Initiative 3 (ADNI3) (68.8-84.6 years of age, male:female=1:1) collected using 3T MRI scanners and the following protocol: T1w MPRAGE: 1 mm³ voxel-size; diffusion-weighted imaging (DWI): 126 diffusion directions, b=2000 s/mm², 2 mm isotropic voxels.
Dataset 2 contained low angular resolution data from 24 non-demented older adults (66.0-84.6 years of age, male:female=1:1) collected using a 3T MRI scanner and the following protocol: T1w MPRAGE: 1 mm³ voxel-size; DWI: 41 directions, b=1000 s/mm², 2 mm isotropic voxels.

Processing
The same data processing pipeline was applied to both datasets. Bias field corrections and brain masking were performed on the T1w images (MASS). ⁶ DWI preprocessing and tensor fitting was performed using TORTOISE.⁷ Intensity-inverted T1w images were used for distortion correction of the DWI data. Multi-tissue constrained spherical deconvolution (MSMT-CSD) ⁸ was used to estimate the fODF of the preprocessed DWI data, with I(max)=8.

Spatial normalization
Iterative fODF-based registration was conducted for group-wise spatial normalization in both datasets, separately, using a symmetric diffeomorphic fODF registration approach. ⁵ Iterative tensor-based registration was also performed in both datasets using DR-TAMAS, one of the top-performing tensor-based registration algorithms. ⁴ The transformations generated from tensor-based registration were applied to the corresponding fODF data.

Analysis
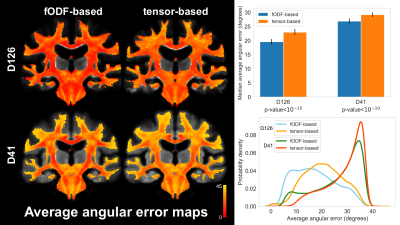
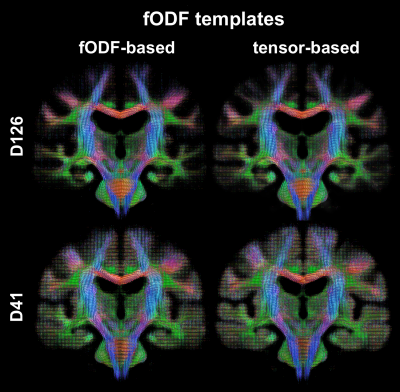
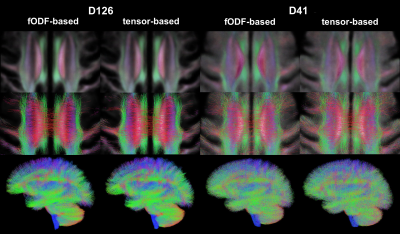
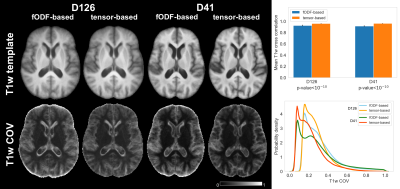
To assess the spatial matching of fODFs after spatial normalization, the angular error between corresponding peaks of fODFs from two participants was calculated in each voxel and was averaged over all possible pairs of participants. Maps of the average angular error were compared across registration approaches. To further assess fODF spatial matching, mean fODF templates were generated, white matter tractography with 500,000 streamlines was performed in the mean fODF templates, and the tractography results were compared across registration approaches. To assess how spatial matching of diffusion information achieved with fODF-based and tensor-based registration translated into matching of brain structural information, the spatial transformations derived from the two registration approaches were applied to corresponding T1w images. Average cross correlations of T1w images over all pairs of participants, as well as the coefficient of variation (COV) of normalized T1w signals were calculated and compared across registration approaches. The above analysis was repeated in both datasets.

Results and Discussion

The average angular error across fODFs was generally lower throughout the brain when using fODF-based compared to tensor-based registration, suggesting superior matching of fODFs when using fODF-based registration (Fig.1). This was anticipated since fODF-based registration aims at minimizing the differences in fODFs across participants, while tensor-based registration does not include fODF information in the cost function. The above was true in both datasets, however the improvement in fODF matching with fODF-based registration was lower in the low angular resolution dataset. fODF templates from different registration methods had few small differences, but were largely similar otherwise, demonstrating that fODF features were generally preserved even with tensor-based registration (Fig.2). Tractography results were more robust and less noisy when using the template developed with fODF-based compared to tensor-based registration. This was true in both high and low angular resolution datasets (Fig.3). Application of the fODF-based and tensor-based transformations onto the corresponding T1w images showed that tensor-based registration resulted in higher average cross correlation of T1w images over all pairs of participants, and lower COV of normalized T1w signals compared to fODF-based registration (Fig.4). This suggests superior structural matching for tensor-based compared to fODF-based registration, which may be due to better spatial matching near the cortex and ventricles facilitated by means of the trace of the diffusion tensor used in tensor-based registration.

Conclusion

This work has achieved a number of goals. First, it increases our confidence in fODF-based registration through comparison to thoroughly evaluated tensor-based registration. Second, it demonstrates that fODF-based registration is robust even in conditions that are optimal for tensor but not fODF reconstruction. Third, it shows that tensor-based registration has the ability to spatially match fODF features rather well, though less accurately than fODF-based registration. Fourth, there is still room for improvement in fODF-based registration, since the generated transformations resulted in worse matching of structural information than tensor-based transformations.

Acknowledgements

This study was supported by National Institutes of Health grant R01AG052200.