Introduction

In the last decade, cardiac MRI became the imaging modality of choice for myocardial function measurements as well as locally resolved tissue characterization. Here, quantitative methods like T₁ and T₂ mapping are useful tools for a precise tissue characterization. Recently, numerous studies explored the alternative contrast mechanism of the spin-lattice relaxation time T_1ρ [1,2,3]. Due to the high sensitivity to low frequency processes at the molecular and cellular level, native T_1ρ-mapping might be superior for accurate tissue characterization. Moreover, T_1ρ gives the possibility for dispersion measurements by manipulation of the effective spin-lock (SL) pulse amplitude, which enables additional contrast mechanisms. However, due to cardiac and respiratory motion, the generation of single myocardial T_1ρ-maps is very time consuming. In consequence, the investigation of myocardial T_1ρ dispersion is not feasible in the limited measurement time of a common in vivo experiment.
In this work, we present a novel concept for myocardial T_1ρ dispersion quantification. Our measurements are based on an accelerated cardiac T_1ρ-mapping sequence and a new approach called dispersion reconstruction.

Theory

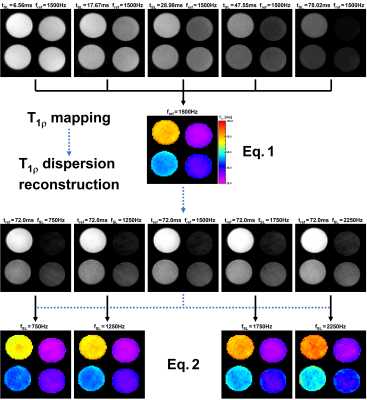
For T_1ρ dispersion imaging, one typically needs to acquire a series of T_1ρ-maps with various SL amplitudes f_SL. With the new T_1ρ dispersion reconstruction approach, a T_1ρ dispersion image can be reconstructed by only acquiring a single T_1ρ-map and a series of dispersion-weighted images (different f_SL, constant SL time t_SL). The concept is illustrated in Fig. 1. First, a reference T_1ρ-map is acquired by varying t_SL (constant amplitude f_SL,const) and fitting a mono-exponential function:
$$I_{map}=I\left(t_{SL},f_{SL,const}\right)=I_0\cdot\text{exp}\left[-\frac{t_{SL}}{T_{1\rho}(f_{SL,const})}\right]\;\;\;\;\;\text{Eq. 1}$$
Subsequently, several dispersion-weighted images are generated by the variation of f_SL at a constant SL time t_SL,const.
$$I_{disp}=I\left(t_{SL,const},f_{SL}\right)=I_0\cdot\text{exp}\left[-\frac{t_{SL,const}}{T_{1\rho}(f_{SL})}\right]$$
It is crucial that one of these images is acquired using the amplitude of the reference T_1ρ-map.
$$I_{ref}=I\left(t_{ref},f_{ref}\right)=I_0\cdot\text{exp}\left[-\frac{t_{ref}}{T_{1\rho}(f_{ref})}\right],\,\,\,t_{ref}=t_{SL,const},\,\,\,f_{ref}=f_{SL,const}$$
Under this condition, a new synthetic T_1ρ-map can be reconstructed from each dispersion-weighted image using the following equation:
$$T_{1\rho}(f_{disp})=\left(\frac{1}{T_{1\rho}(f_{ref})}-\frac{1}{t_{ref}}\cdot\text{log}\left[\frac{I_{disp}}{I_{ref}}\right]\right)^{-1}\;\;\;\;\;\text{Eq. 2}$$
The information thus obtained can then be used to calculate a dispersion map by pixel-wise fitting a suitable dispersion model (e.g. linear function).

Methods

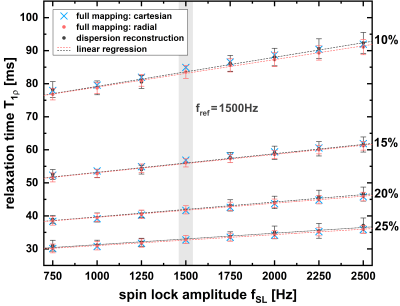
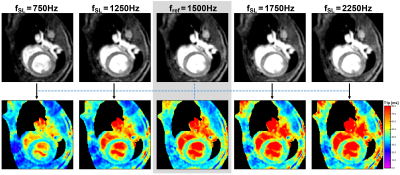
All measurements were performed on a 7.0T small animal imaging system (Bruker BioSpec 70/30, BioSpin MRI GmbH, Ettlingen, Germany). Our novel dispersion reconstruction approach was validated in phantom as well as in in vivo experiments. T_1ρ preparation was performed by totally-balanced-spin-locking (TB-SL) [4]. Acquisition of k-space was optimized for very fast myocardial imaging using a radial spoiled gradient echo readout (T_E=1.9ms, T_R=4.7ms). For every T_1ρ-prepared image, data acquisition was segmented into 13 preparation experiments (identical t_SL and f_SL), each separated by a waiting time t_rec for magnetization recovery. Depending on the imaging mode, 8 different SL-prepared images with different t_SL (T_1ρ-mapping) respectively f_SL (dispersion-weighting) were acquired.
In the phantom measurements, 4 cylindrical sample tubes with various BSA concentrations were investigated and the dispersion reconstruction approach was compared with two common full-mapping techniques, once using the accelerated radial readout and once a conventional cartesian readout (in which 8 complete T_1ρ-maps needs to be acquired). The waiting time t_rec was adjusted to 1000ms resulting in total measurement times of 3.5min (novel approach), 13.9min (full-mapping radial method) and 25.6min (full-mapping cartesian method). For the in vivo measurements, one SL preparation was performed in one heart beat (during end diastole) per respiratory cycle. Here, t_rec resulted in approximately 1100ms. A T_1ρ-map and a synthetic T_1ρ dispersion image was generated for testing the practicability and for investigation of the achievable image quality in vivo.

Results

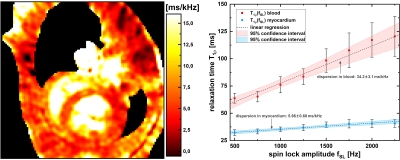
Fig. 2 shows the results of the phantom measurements. It is apparent that the common full-mapping cartesian and radial T_1ρ dispersion methods as well as the novel dispersion reconstruction approach produce identical results with high reproducibility and accuracy. Mean deviation was 0.82%, 0.91%, 1.23% and 1.63% for the four different BSA phantoms. In Fig. 3 and 4 the results of the in vivo measurements are shown. In Fig. 3 the dispersion-weighted images and the reconstructed synthetic T_1ρ-maps are depicted. Fig. 4 shows a synthetic T_1ρ dispersion image and the determined dispersion behaviour of blood and myocardium. In myocardial tissue, T_1ρ values increased from a minimum of 29.5ms to a maximum of 44.3ms with a mean slope of 5.66±0.60ms/kHz. The mean slope in the blood pool was determined to be 34.2±3.1ms/kHz.

Discussion

In this work, a new synthetic dispersion imaging method is presented that is multiple times faster than common full-mapping techniques by comparable accuracy and usability. This acceleration is based on two steps. First, an acceleration of data sampling using optimized radial imaging, and second the implementation of the dispersion reconstruction procedure. Compared to the common cartesian full-mapping method, an acceleration by a factor of 7.4 was achieved. Furthermore, the experiments confirm the applicability of our new method in vivo, which enables the inclusion of T_1ρ dispersion imaging in a conventional MRI study protocol. Due to the promising results using our new method, further studies on mice are in preparation for investigating the dispersion character of healthy and various diseased tissues. Moreover, our novel method is also feasible in clinical human MRI examinations, which are also planned in the near future.

Acknowledgements

This work was supported by the Federal Ministry for Education and Research of the Federal Republic of Germany (BMBF 01EO1504, MO6)