0521

OG-DNN: Orientation-Grasp Deep Neural Network for Quantitative Susceptibility Mapping
Kuo-Wei Lai1,2, Jeremias Sulam1, Manisha Aggarwal3, Peter van Zijl2,3, and Xu Li2,3
1Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, United States, 2F.M. Kirby Research Center for Functional Brain Imaging, Kennedy Krieger Institute, Baltimore, MD, United States, 3Department of Radiology and Radiological Sciences, Johns Hopkins University, Baltimore, MD, United States

Synopsis

We designed a method called Orientation-Grasp Deep Neural Network (OG-DNN) for Quantitative Susceptibility Mapping (QSM). OG-DNN has dynamically adaptive convolutional filters that adjust themselves according to the input B0 orientation in the subject frame of reference. Our experimental results demonstrate that OG-DNN can reconstruct high-quality and consistent susceptibility maps from MR phase data acquired at different head orientations with respect to B0 within a consistent subject frame of reference. OG-DNN is expected to provide improved flexibility in practice and may potentially facilitate the development of deep learning-based Susceptibility Tensor Imaging (STI) reconstructions.

Introduction

Quantitative Susceptibility Mapping (QSM) aims at imaging the tissue magnetic susceptibility from MR phase measurements by solving an ill-posed dipole inversion problem.1, 2 Conventional methods either utilize multiple phase measurements at different head orientations to fill in the region with singularity in the dipole kernel, i.e. the COSMOS method,3 or use regularized iterative methods to mitigate the streaking artifacts induced by direct dipole inversion using single orientation phase data.4-6 COSMOS QSM exhibits excellent image quality, but is expensive in terms of data acquisition, while single orientation iterative methods usually need parameter tuning and may introduce extra smoothing effects according to the regularization constrains. Recently, deep learning-based QSM methods e.g. QSMnet7 and DeepQSM8 have shown the capability of performing QSM dipole inversion to generate high-quality, e.g. COSMOS like, QSM reconstruction, using phase maps from only a single orientation. However, all these approaches are constrained to training the neural network model with a fixed dipole kernel, i.e. with a fixed B0 orientation in the lab frame of reference, which limits the flexibility in practical use. In this work, we present an orientation-adaptive alternative which adapts to different dipole kernels corresponding to different orientations of the main magnetic field in the subject frame. This method achieves comparable reconstruction performance compared to QSMnet. In addition, this method may be useful in the potential design of deep learning-based reconstruction with more complex models such as STI.9

Methods

For training and testing data pairs, we collected a total of 31 MR phase measurements acquired at 7T (Philips Achieva, 32 channel head coil) with two 3D GRE sequences with 1 mm isotropic resolution on 7 healthy subjects (5 orientations for 3 subjects with TR=28 ms, TE1/ΔTE=5/5 ms, 5 echoes, 4 orientations for another 4 subjects with TR=45 ms, TE1/ΔTE=2/2 ms, 9 echoes). The study was IRB approved and informed consent was obtained from all participants. The corresponding COSMOS were reconstructed for each subject after multiple steps of phase preprocessing including best-path based phase unwrapping10 and V-SHARP11 for removing the background and echo averaging for echoes with TEs between 10 ms and 30 ms. We also augmented our dataset by generating 31 simulated local phase maps at random head orientations (within ±45° to z-axis) using the 7 COSMOS. For this stage of our study, five subjects were used for training, and two subjects for validation. Full leave-one-out cross-validation will be employed in follow-up work. Inspired by studies on image super-resolution and dynamic filter learning,12, 13 we included a dedicated adaptable module capable of handling different B0 orientations in the subject frame, i.e. different dipole kernels, making the overall architecture more applicable in practice. The proposed OG-DNN model (Figure 1) contains a primary fully convolutional neural network and an Orientation-Grasp Module. The primary fully convolutional neural network is composed of stacks of wide-dropout residual blocks14 and takes local phase measurements as input. The Orientation-Grasp Module, by taking different B0 directions as input, predicts varying weights of orientation-adaptive convolutional filters after the primary neural network. We trained our OG-DNN with an L1 loss and Stochastic Gradient Descent (SGD) using 3D patch data with a size of 64×64×64 voxels. The training time is approximately 48hr and the reconstruction time is 8s per image. We compared the results of our method with QSMnet and conventional methods including TKD4 and MEDI15 using the validation set in the next section.

Results

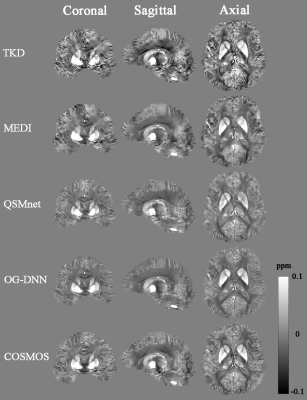
Table 1 summarizes the QSM reconstruction results on our validation set using different methods evaluated by quantitative performance metrics, Normalized Root Mean Square Error (NRMSE), Peak Signal-to-Noise Ratio (PSNR), High Frequency Error Norm (HFEN), and Structural Similarity Index (SSIM). COSMOS is treated as the gold standard reconstruction ground-truth for all metric evaluations. These results show that our OG-DNN achieves a PSNR of 39.24dB which is comparable to QSMnet performance. Figure 2 displays the three plane views of QSM maps from one subject in the validation set reconstructed using different methods. The result of OG-DNN has significantly less artifacts and is also the closest to COSMOS. Figure 3 displays results of one validation example with input local phase acquired at 5 different head orientations using different methods, demonstrating that the results from OG-DNN are consistent across different orientations.

Discussion

Compared to current deep learning-based QSM methods, our OG-DNN QSM method not only learns the dipole kernel inversion, but also provides more flexibility in training and deployment. It can be directly trained and applied on registered phase data in a consistent subject frame. On the contrary, previous methods, e.g. such as QSMnet, assume a fixed B0 direction, e.g. in the z-axis, thus only learn the deconvolution of a fixed dipole kernel. Additionally, the proposed OG-DNN should be tested with more diverse orientations with large rotation angles to further demonstrate the capability of the Orientation-Grasp Module.

Conclusion

We have developed an OG-DNN model for QSM reconstruction, and demonstrated its capability of adapting to different orientations of the main magnetic field in the subject frame of reference, thus different dipole kernels. Such network design might facilitate future development of deep learning-based STI which has to incorporate MR phase data acquired at different head orientations to estimate tissue susceptibility tensors.

Acknowledgements

Funding support: NCRR and NIBIB (P41 EB015909).

References

1. Yi Wang and Tian Liu. Quantitative susceptibility mapping (qsm): decoding mri data for a tissue magnetic biomarker. Magnetic resonance in medicine, 73(1):82–101, 2015.

2. Chunlei Liu, Wei Li, Karen A Tong, Kristen W Yeom, and Samuel Kuzminski. Susceptibility-weighted imaging and quantitative susceptibility mapping in the brain. Journal of magnetic resonance imaging, 42(1):23–41, 2015.

3. Tian Liu, Pascal Spincemaille, Ludovic De Rochefort, Bryan Kressler, and Yi Wang. Calculation of susceptibility through multiple orientation sampling (cosmos): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in mri. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 61(1):196–204, 2009.

4. Karin Shmueli, Jacco A de Zwart, Peter van Gelderen, Tie-Qiang Li, Stephen J Dodd, and Jeff H Duyn. Magnetic susceptibility mapping of brain tissue in vivo using mri phase data. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 62(6):1510–1522, 2009.

5. Christian Langkammer, Ferdinand Schweser, Karin Shmueli, Christian Kames, Xu Li, Li Guo, Carlos Milovic, Jinsuh Kim, Hongjiang Wei, Kristian Bredies, et al. Quantitative susceptibility mapping: report from the 2016 reconstruction challenge. Magnetic resonance in medicine, 79(3):1661–1673, 2018.

6. Andreas Deistung, Ferdinand Schweser, and Ju¨rgen R Reichenbach. Overview of quantitative susceptibility mapping. NMR in Biomedicine, 30(4):e3569, 2017.

7. Jaeyeon Yoon, Enhao Gong, Itthi Chatnuntawech, Berkin Bilgic, Jingu Lee, Woojin Jung, Jingyu Ko, Hosan Jung, Kawin Setsompop, Greg Zaharchuk, et al. Quantitative susceptibility mapping using deep neural network: Qsmnet. NeuroImage, 179:199–206, 2018.

8. Steffen Bollmann, Kasper Gade Bøtker Rasmussen, Mads Kristensen, Rasmus Guldhammer Blendal, Lasse Riis Østergaard, Maciej Plocharski, Kieran O’Brien, Christian Langkammer, Andrew Janke, and Markus Barth. Deepqsm-using deep learning to solve the dipole inversion for quantitative susceptibility mapping. NeuroImage, 195:373–383, 2019.

9. Wei Li, Chunlei Liu, Timothy Q Duong, Peter CM van Zijl, and Xu Li. Susceptibility tensor imaging (sti) of the brain. NMR in Biomedicine, 30(4):e3540, 2017.

10. Hussein Abdul-Rahman, Munther Gdeisat, David Burton, and Michael Lalor. Fast three-dimensional phase-unwrapping algorithm based on sorting by reliability following a non-continuous path. In Optical Measurement Systems for Industrial Inspection IV, volume 5856, pages 32–40. International Society for Optics and Photonics, 2005.

11. Bing Wu, Wei Li, Arnaud Guidon, and Chunlei Liu. Whole brain susceptibility mapping using compressed sensing. Magnetic resonance in medicine, 67(1):137–147, 2012

12. Xuecai Hu, Haoyuan Mu, Xiangyu Zhang, Zilei Wang, Tieniu Tan, and Jian Sun. Meta-sr: A magnification-arbitrary network for super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 1575–1584, 2019.

13. Xu Jia, Bert De Brabandere, Tinne Tuytelaars, and Luc V Gool. Dynamic filter networks. In Advances in Neural Information Processing Systems, pages 667–675, 2016.

14. Sergey Zagoruyko and Nikos Komodakis. Wide residual networks. arXiv preprint arXiv:1605.07146, 2016.

15. Jing Liu, Tian Liu, Ludovic de Rochefort, James Ledoux, Ildar Khalidov, Weiwei Chen, A John Tsiouris, Cynthia Wisnieff, Pascal Spincemaille, Martin R Prince, et al. Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map. Neuroimage, 59(3):2560–2568, 2012.

Figures

Figure 1: Network architecture of OG-DNN. The Primary fully convolutional neural network contains one convolutional layer and one ReLU at the beginning followed by 9 stacks of residual blocks with wide-dropout design. Each residual block contains 2 convolutional layers, 2 batch normalization layers, and 2 ReLU layers with 1 skip connection for residual learning. The Orientation-Grasp Module is a 4-layer Multi-Layer Perceptron (MLP). The output of the Orientation-Grasp Module is the orientation-adaptive convolutional filter added at the end of the OG-DNN.

Table 1: Quantitative performance metrics, Normalized Root Mean Square Error (NRMSE), Peak Signal-to-Noise Ratio (PSNR), High Frequency Error Norm (HFEN), and Structural Similarity Index (SSIM), for QSM reconstruction performance evaluation of different methods using the validation set. All metrics use COSMOS as gold standard ground-truth to calculate quantitative indexes. OG-DNN shows comparable performance with QSMnet and outperforms TKD and MEDI.

Figure 2: Three plane views of example QSM maps reconstructed using different methods. OG-DNN result shows high-quality COSMOS-like reconstruction performance. The TKD reconstruction suffers from streaking artifacts, while MEDI shows some over smoothing.

Figure 3: Coronal view of the QSM maps reconstructed from MR phase measurements collected at five head orientations of a single subject using different methods. The TKD results show streaking artifacts while MEDI shows less clear anatomical contrast especially around the cortical regions. On the other side, OG-DNN and QSMnet show consistent COSMOS-like results for different orientations.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
0521