0519
A non-local filtering based approach for high quality quantitative susceptibility mapping reconstruction1Radiology, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, United States, 2Bioengineering, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, United States, 3Psychiatry, University of Pennsylvania, Philadelphia, PA, United States
Synopsis
This abstract presents a novel non-local filtering based reconstruction approach for high quality quantitative susceptibility mapping (QSM). Popular QSM techniques that use fixed sparsity priors such as total variation or total generalized variation often suffer from blurring of fine features (e.g. edges). Since QSM images have non-local spatial redundancies in the form of self-similarity, we develop an approach that uses non-local grouping by 4D cube-matching and collaborative filtering in a plug-and-play (PnP) alternating direction method of multiplier (ADMM) framework. We show that the proposed non-local filtering based reconstruction approach achieves sharper edges and better preservation of fine features.
Introduction
Quantitative susceptibility mapping (QSM) [1,2] is non-invasive imaging technique that maps tissue magnetic properties and has been applied to stroke [1], impaired tissue oxygen consumption and neuronal demyelination research [1]. QSM reconstruction remains challenging as it requires finding the solution to an ill-posed inverse problem. Although several techniques use sparsifying constraints such as total variation (TV) [3] and total generalized variation (TGV) [4,5], QSM images are highly textured and these techniques can cause smoothing of edges, blurring of fine features and loss of contrast. Patch-based denoising techniques leverage non-local spatial redundancies to remove noise [6-10]. Recently, a plug-and-play (PnP) alternating direction method of multipliers (ADMM) [11] technique was developed to allow the use of denoising priors for ill-posed inverse problems. We use 4D block matching and collaborative filtering (BM4D) [9] as the non-local filtering technique and combine it with PnP-ADMM approach to achieve a novel non-local filtering reconstruction for QSM. We compared its performance to multi-orientation QSM (COSMOS) and several compressive sensing (CS) algorithms [3-5] using the ISMRM 2016 challenge dataset and in patients with hemorrhagic glioblastoma with scoring by an expert radiologist and quantitative image metrics.Methods
The constrained reconstruction formulation we aim to minimize is $$min_{\chi} \theta (\chi) \textit{ s.t. } ||M(F^{H}DF\chi-\phi)||^{2}_{2} \leq \sigma ^{2} \textit{(1)}$$Here M is a spatially varying weight, D is the dipole kernel in Fourier domain, χ the magnetic susceptibility, F is the Fourier operator, FH is the inverse Fourier operator, ϕ is the tissue phase, σ is the noise standard deviation and θ(χ) is a data regularization term. Using Bregman iterations [12], Eq. (1) can be rewritten as
$$min_{\chi} \theta (\chi) + \frac{\mu}{2}||M(F^{H}DF\chi-\phi^{k+1})||^{2}_{2}\textit{(2)}$$
$$\phi^{k+1}=\phi^{k}+(\phi - F^{H}DF\chi^{k})\textit{(3)}$$
The iterative update of ϕ in Eq. (3) is the “adding noise back” step [12], which helps prevent smoothing edges and fine features due to regularization. Using a PnP-ADMM framework [11], enforcing variable substitution and using denoiser (D) instead of the spatial prior θ(χ); Eq. 2 can be written as
$$\chi=min_{\chi} \frac{\alpha}{2}||\chi-v+u||^{2}_{2} + \frac{\mu}{2}||M(F^{H}DF\chi-\phi^{k+1})||^{2}_{2}\textit{(4)}$$
$$v=min_{v} D_{\sigma}(\chi+u)\textit{(5)}$$
$$u^{n+1}=u^{n}+(\chi^{n+1}-v^{n+1})\textit{(6)}$$
Here D is the BM4D collaborative filtering denoiser [9] and u is a scaled Lagrange multiplier [11]. We compare the results of our proposed collaborative filtering approach (PnP-BM4D) to thresholded k-space division (TKD) [3], closed-form L2-regularized inversion [3], morphology enabled dipole inversion (MEDI) [4,13] and non-linear MEDI with TGV constraints (FANSI-TGV) [4]. Performance of the recosntruction techniques were tested on the 2016 ISMRM QSM challenge data using several global image quality metrics [5] and quantification of mean susceptibilities from ROI’s. Results from the single-echo gradient-echo MRI obtained on 4 patients with tumor lesions were scored by an expert reviewer (Scale 1-3; 1= least, 3=most) for overall image quality (IQ), vessel sharpness (VS), and sharpness of features in the tumor (TS). Amount of blurring was quantified using blur metric [14].
Results
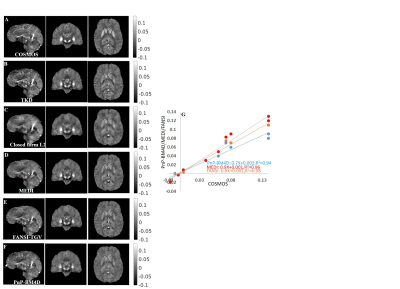
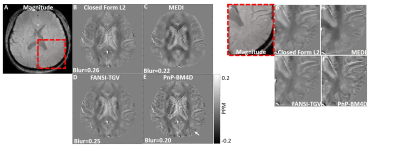
A comparison of the different reconstructions techniques on the 2016 ISMRM QSM challenge data are shown in Fig (1). TKD (SSIM=0.75,RMSE=73.1,HFEN=66.7) and closed-form L2 reconstructions (SSIM=0.81,RMSE=70.1,HFEN=65.1) performed poorly when compared to multi-orientation COSMOS. PnP-BM4D (SSIM=0.85,RMSE=61.9,HFEN=59.1,MI=0.47) and FANSI-TGV (SSIM=0.85,RMSE=61.2,HFEN=61.1,MI=0.46) had improved performance as compared to MEDI (SSIM=0.84,RMSE=60.1,HFEN=65.9,MI=0.45), though sharp features such as veins were better preserved in PnP-BM4D. Overall, the mean magnetic susceptibilities calculated from PnP-BM4D, FANSI-TGV and MEDI exhibit good correlation with the multi-orientation COSMOS. In patient with tumor lesions (Fig. 2) PnP-BM4D (IQ=3,VS=3,TS=3) outperformed closed-form L2 (IQ=1.75±0.43,VS=1.25±0.43,TS=1.5±0.5), MEDI (IQ=2.25±0.43,VS=2.5±0.5,TS=2.5±0.5) and FANSI-TGV (IQ=2.25±0.43,VS=2.25±0.43,TS=2.5±0.5). As seen in Fig 3, PnP-BM4D (blur=0.21±0.01) achieved sharper reconstruction with high vessel conspicuity and excellent contrast when compared closed-form L2 (blur=0.29±0.03), MEDI (blur=0.24±0.01) and FANSI-TGV (blur=0.26±0.02) reconstructions.Discussion
Non-local filtering using 4D block matching showed good recovery of magnetic susceptibility compared to the multi-orientation standard while preserving high resolution features such as vessels without degradation. The effectiveness of 4DBM appears to be closely related to the structural similarity of remote cortical grey and white matter structures. Similar 3D QSM image patches appear to show a highly sparse representation that can be exploited using non-local filtering and reducing artifacts associated with the ill-posed inverse problem. Existing QSM techniques use spatial edge-priors extracted from T2* magnitude images to prevent smoothing of edges. These images may have distinct morphology compared to the reconstructed susceptibility maps and the mismatch can cause smoothing of features. The proposed technique does not use spatial gradients as sparsifying transform and also does not depend on spatial edge-priors from magnitude images to prevent smoothing of edges. Instead, we use non-local redundancies and similarities among various parts of the image. The adding-noise-back step (Eq. 3) helps ensure that features lost to filtering are added back to the reconstruction formulation. The PnP-ADMM formulation allows for the use of this collaborative filtering approach in a CS framework for QSM.Conclusion
We developed a novel non-local filtering approach for high quality QSM reconstructions. We used a state-of-the-art denoising technique, BM4D, in a QSM reconstruction framework using a PnP ADMM implementation. The proposed technique does not need spatial edge-priors extracted from the magnitude image to improve QSM reconstructions. High image quality reconstructions with improved vessel conspicuity, better preservation of fine features in the tumoral region and improved contrast near remote cortical grey and white matter structures is enabled by the proposed non-local filtering based formulation.Acknowledgements
This work is supported by R00-HL108157, McCabe Foundation, and W.W. Smith Foundation.References
1.Chang S,
Zhang J, Liu T, Tsiouris A J, Shou J, Nguyen T and Kovanlikaya I. (2016).
Quantitative Susceptibility Mapping of Intracerebral Hemorrhages at Various
Stages. JMRI, 44(2), 420–425.
2. Wang Y
and Liu T. (2015), Quantitative susceptibility mapping (QSM): Decoding MRI data
for a tissue magnetic biomarker. Magn. Reson. Med., 73: 82–101.
doi:10.1002/mrm.25358.
3. Bilgic B, Chatnuntawech I, Fan A P, Setsompop K, Cauley S F, Wald L L and Adalsteinsson E. (2014), Fast image reconstruction with L2-regularization. J. Magn. Reson. Imaging, 40: 181–191. doi:10.1002/jmri.24365.</p>
4. Milovic
C, Bilgic B, Zhao B, Acosta-Cabronero J and Cristian Tejos, Fast nonlinear
susceptibility inversion with variational regularization, Magn. Reson. Med. 2018:
80(2):814-821, doi: 10.1002/mrm.27073.
5. Langkammer C, Schweser F, Shmueli K, Kames C, Li X, Guo L, Milovic C, Kim J., Wei H, Bredies K, Buch S, Guo Y, Liu Z, Meineke J, Rauscher, A., Marques, J. P. and Bilgic, B. (2017), Quantitative susceptibility mapping: Report from the 2016 reconstruction challenge. Magn. Reson. Med. doi:10.1002/mrm.26830.
6. Buades A, Coll B and Morel J-M. A non-local algorithm for image
denoising. Proceedings of the 2005 IEEE Computer Society Conference on Computer
Vision and Pattern Recognition (CVPR'05),V2;P60-65.
7. Awate S, Whitaker R. Higher-Order Image Statistics for Unsupervised, Information-Theoretic, Adaptive Image Filtering IEEE Computer Vision & Pattern Recognition (CVPR), June 2005, vol 2, pp 44-5.
8. Dabov K, Foi A, Katkovnik V, and Egiazarian K. Image denoising with block-matching and 3D filtering. Proc. SPIE Electronic Imaging '06, no. 6064A-30, San Jose, California, USA, January 2006.
9. Maggioni M, Katkovnik V, Egiazarian K, and Foi A. A Nonlocal Transform-Domain Filter for Volumetric Data Denoising and Reconstruction. IEEE Trans. Image Process., vol. 22, no. 1, pp. 119-133, January 2013.
10. Alkinani M, El-Sakka M. Patch-based models and algorithms for image denoising: a comparative review between patch-based images denoising methods for additive noise reduction. J Image Video Proc. 2017, 58 (2017) doi:10.1186/s13640-017-0203-.
11. Chan S, Wang X, Elgendy O, "Plug-and-Play ADMM for image restoration: Fixed point convergence and applications," IEEE Transactions on Computational Imaging, Nov. 2016.
12.
Goldstein T, Osher S. The Split Bregman Method for L1-Regularized
Problems, SIAM Journal on Imaging
Sciences 2009 2:2, 323-343.
13. Liu T, Liu J, de Rochefort L, Spincemaille P, Khalidov I, Ledoux JR, Wang Y. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: comparison with COSMOS in human brain imaging. Magnetic Resonance in Medicine. 2011; 66(3):777–783.
14. Crete F, Dolmiere T, Ladret P, and Nicolas M. The blur effect: perception and estimation with a new no-reference perceptual blur metric. Proc. SPIE 6492, Human Vision and Electronic Imaging XII, 64920I.
Figures