0517
Correcting gradient chain-induced fat quantification errors in multi-echo SoS acquisition using the gradient impulse response function1Department of Diagnostic and Interventional Radiology, School of Medicine, Technical University of Munich, Munich, Germany, 2Philips Research Laboratory, Hamburg, Germany
Synopsis
Multi-echo Stack-of-stars-type radial k-space trajectories employing golden-angle ordering have been becoming popular for abdominal fat quantification. Gradient chain imperfections including eddy currents and gradient delays are known to affect the image quality of radial imaging. Most methods for compensating radial k-space trajectory errors are based either on the acquisition of calibration lines with opposite polarity or on the processing of approximately anti‐parallel spokes from the actual radial acquisition. This work shows that a trajectory correction based on a gradient system impulse response function improves fat quantification in gated golden-angle radial Dixon imaging.
Purpose
Phase errors induced by eddy currents have been shown to induce a bias in abdominal fat quantification using Cartesian complex-based chemical shift encoding-based water–fat separation techniques [1-3]. Multi-echo radial stack-of-stars (SoS) acquisitions have been recently applied for abdominal fat quantification in patients with difficulty in performing breath-holds [4-5]. Gradient chain imperfections including eddy currents and gradient delays are known to affect the image quality of radial imaging [6, 7]. When radial k-space trajectories are used for chemical shift encoding-based water-fat separation, gradient chain imperfections are expected to affect both the image quality of the source multi-echo images and induce bias in the fat fraction. Previous methods for compensating for such gradient chain imperfections in radial water-fat imaging have mainly focused on the determination of gradient timing errors based on the acquisition of calibration lines with opposite polarity [4]. However, the acquisition of such calibration lines would need to be repeated for every scan. An alternative approach to correct for gradient chain errors would be the acquisition of the gradient system impulse response function (GIRF) [8] based on a calibration measurement performed once for the system [9, 10]. The purpose of the present work is to correct gradient chain-induced fat quantification errors in multi-echo radial stack-of-stars acquisition based on the GIRF measured using a thin slice method.Methods
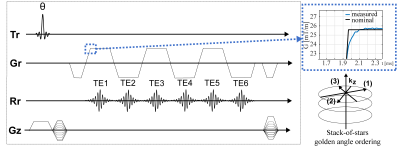
Trajectory Correction:Figure 1 shows the employed stack-of-stars six-echo pulse sequence. A phantom-based measurement of the GIRF using a thin-slice method as proposed in [11] was used to characterize the gradient system. The magnitude and phase of the first order components of the GIRF were used for the correction of the readout gradient by convolving the GIRF with the input gradient waveform (Figure 1).
Simulation:
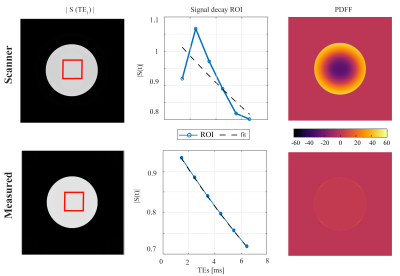
Simulated k-space data of a circular numerical phantom was generated by using the NUFFT (BART, https://mrirecon.github.io/bart/) based on the measured, GIRF corrected, k-space trajectories according to the 6-echo sequence from Figure 1. Including a 20 ms T2* decay, the images were reconstructed using the default scanner k-space trajectory and the measured trajectory. Complex-based water–fat separation was performed using a multi-peak fat spectrum and a single T2* decay [12] and PDFF maps were determined subsequently using the magnitude discrimination approach [13].
Phantom measurement:
A water bottle phantom was scanned with a 3D SoS bipolar 6-echo gradient-echo sequence (Figure 1) using a 16-channel anterior coil with TE: [1.5/2.6/3.7/4.8/5.9/7.0] ms, TR: 14 ms, flip angle: 3°, in-plane resolution: 1.5x1.5x3 mm3, FOV: 300x300x200 mm3
In vivo measurement:
A gated 3D SoS bipolar 6-echo gradient-echo (Figure 1) abdominal measurement was performed on three volunteers using a 16-channel anterior coil with TE: [1.4/2.4/3.4/4.5/5.5/6.6] ms, TR: 10 ms, flip angle: 10°, in- plane resolution: 1.5x1.5x3 mm3, FOV: 450x450x100 mm3, duration: 7 min. A single-min-cut graph-cut with variable layer graph construction [14] was used to estimate the field map to initialize a complex-based water–fat separation. Cartesian breath-hold scans were used as a reference for generated PDFF maps.
Results
Simulation:Figure 2 shows the effect of the trajectory imperfections on the magnitude of the echo images. The echo magnitude images reconstructed with the uncorrected trajectories appeared less homogeneous than the GIRF-corrected ones. The magnitude signal decay over echo time was also better fitted by an exponential decay for the GIRF-corrected case, resulting in an incorrect water–fat separation result for the uncorrected echo data and large PDFF errors up to 45% in the simulation.
Phantom measurement:
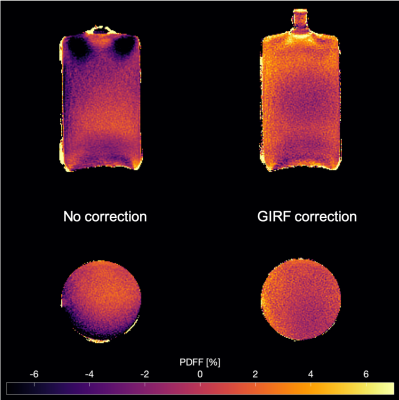
Figure 3 shows PDFF maps of the water bottle phantom scanned in transversal and coronal orientation. PDFF maps from the uncorrected scans showed significant intensity inhomogeneities over the whole FOV, extending to negative PDFF values down to -11%. Correcting the trajectory with the measured GIRF resulted in a more homogeneous PDFF and close to zero within the bottle.
In vivo measurement:
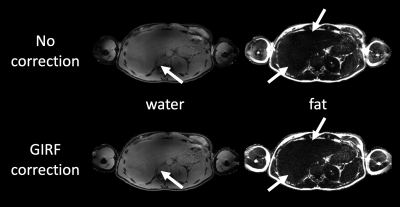
The effect of the GIRF correction on water–fat separation results is shown in Figure 4 for one subject. The GIRF-corrected water image illustrates the deblurring by the GIRF correction. Intensity inhomogeneities in the fat image were also adjusted by the proposed method. Figure 5 shows abdominal PDFF maps for three volunteers. Negative underestimations of the PDFF down to -30% towards the liver edge could be adjusted with the GIRF. Comparison of ROIs showed that the corrected PDFF maps agreed better to the PDFF from reference cartesian breath hold scans.
Discussion & Conclusion
Eddy currents and system delays lead to artifacts in radially sampled images and induce a bias in the PDFF estimation. The present work shows that GIRF-corrected SoS trajectories improve blurring caused by trajectory imperfections as well as PDFF estimation by removing biases induced by the different radial k-space trajectory polarity between odd and even echoes. However, the proposed GIRF correction does no correct for phase errors due to motion. A GIRF-based correction of the SoS trajectory should therefore be considered as a fast and reliable principle to increase water-separated image quality and maintain PDFF mapping accuracy when performing gated or free-breathing SoS Dixon acquisitions.Acknowledgements
The present work was supported by the German Research Foundation (SFB824/A9), the European Research Council (grant agreement No 677661, ProFatMRI) and Philips Healthcare. This work reflects only the authors view and the funders are not responsible for any use that may be made of the information it contains.References
[1] H. Yu, A. Shimakawa, C. A. McKenzie, W. Lu, S. B. Reeder, R. S. Hinks, and J. H. Brittain, “Phase and amplitude correction for multi-echo water-fat separation with bipolar acquisitions.,” J Magn Reson Imaging, vol. 31, no. 5, pp. 1264–1271, May 2010.
[2] D. Hernando, C. D. G. Hines, H. Yu, and S. B. Reeder, “Addressing phase errors in fat‐water imaging using a mixed magnitude/complex fitting method,” Magn Reson Med, vol. 67, no. 3, pp. 638–644, Mar. 2012.
[3] S. Ruschke, H. Eggers, H. Kooijman-Kurfuerst, M. N. Diefenbach, T. Baum, A. Haase, E. J. Rummeny, H. H. Hu, and D. C. Karampinos, “Correction of phase errors in quantitative water–fat imaging using a monopolar time-interleaved multi-echo gradient echo sequence,” Magn Reson Med, vol. 78, no. 3, pp. 984–996, Sep. 2017.
[4] T. Armstrong, I. Dregely, A. Stemmer, F. Han, Y. Natsuaki, K. Sung, and H. H. Wu, “Free‐breathing liver fat quantification using a multiecho 3D stack‐of‐radial technique,” Magn Reson Med, vol. 34, p. 274, Apr. 2017.
[5] T. Armstrong, K. V. Ly, S. Murthy, S. Ghahremani, G. H. J. Kim, K. L. Calkins, and H. H. Wu, “Free-breathing quantification of hepatic fat in healthy children and children with nonalcoholic fatty liver disease using a multi-echo 3-D stack-of-radial MRI technique,” Pediatr Radiol, vol. 48, no. 7, pp. 941–953, Jul. 2018.
[6] D. C. Peters, J. A. Derbyshire, and E. R. McVeigh, “Centering the projection reconstruction trajectory: Reducing gradient delay errors,” Magn Reson Med, vol. 50, no. 1, pp. 1–6, Jul. 2003.
[7] K.T. Block, M. Uecke, "Simple method for adaptive gradient‐delay compensation in radial MRI", Proc Intl Soc Mag Reson Med, Montreal. 2011;2816.
[8] S. J. Vannesjo, M. Haeberlin, L. Kasper, M. Pavan, B. J. Wilm, C. Barmet, and K. P. Pruessmann, “Gradient system characterization by impulse response measurements with a dynamic field camera,” Magn Reson Med, vol. 69, no. 2, pp. 583–593, Feb. 2013.
[9] J. Rahmer, P. Mazurkewitz, P. Börnert, and T. Nielsen, “Rapid acquisition of the 3D MRI gradient impulse response function using a simple phantom measurement.,” Magn Reson Med, vol. 28, no. 90, p. 141, Jul. 2019.
[10] J. H. Duyn JH,, Y. Yang Y,, J. A. Frank JA, Van Der, and J. W. van der Veen JW. , “Simple Correction Method for kfork-Space Trajectory Deviations in MRI.,” J. Magn. Reson.., vol. 132, no. 1, pp. 150–153, May 1998;132(1):150-153. doi:10.1006/jmre.1998.1396.
[11] P. Mazurkewitz, J. Rahmer, P. Börnert P. "GIRF measurement using a combination of triangular and chirp waveform input functions," Proc. Joint Annual Meeting ISMRM-ESMRMB, Paris. 2011;0169. [12] Yu, Multiecho Water-Fat Separation and Simultaneous R*2 Estimation With Multifrequency Fat Spectrum Modeling
[12] H. Yu, A. Shimakawa, C. A. McKenzie, E. Brodsky, J. H. Brittain, and S. B. Reeder, “Multiecho water‐fat separation and simultaneous R 2* estimation with multifrequency fat spectrum modeling,” Magn Reson Med, vol. 60, no. 5, pp. 1122–1134, Nov. 2008.
[13] Fat Quantification WithC.-Y. Liu, C. A. McKenzie, H. Yu, J. H. Brittain, and S. B. Reeder, “Fat quantification with IDEAL Gradient Echo Imaginggradient echo imaging: Correction of Bias Frombias from T1 and Noisenoise,” Magn Reson Med, vol. 58, no. 2, pp. 354–364, Aug. 2007.
[14] C. Böhm, M. N. Diefenbach, A. Haase, and D. C. Karampinos, "Accelerated Single-Min-Cut Graph-Cut Algorithm Using a Variable-Layer Graph Construction Improves Field-Mapping in Water–Fat Regions," Proc Intl Soc Mag Reson Med, Montreal. 2019;4007.
Figures