Introduction

Chemical exchange saturation transfer (CEST) imaging [1] enables in vivo detection of intracellular metabolites. While compensation for B₀ inhomogeneity is routine, CEST contrast is highly sensitive to B₁ variations ([2]; see also abstract #5033) for which compensatory approaches are only recently emerging. Parallel transmit methods have been developed but require specialized hardware, while post-processing corrections [3,4] require steady saturation conditions and knowledge of chemical pool parameters, and their efficacy depends on the specific saturation and imaging parameters. Here we propose a new approach, which is to use a tailored spectral-spatial pulse to produce a flat flip angle profile in the presence of B₁ inhomogeneity for more uniform saturation in the heart at 3T.

Methods

RF Pulse Design: Figure 1 illustrates the tailored spectral-spatial pulse construction. The pulse comprises a train of identical spatially-selective subpulses played during trapezoidal gradients. The subpulse is designed by solving:
$$\hat{\textbf{b}} = argmin_{\textbf{b}}{\|1-\textbf{Ab}\|_2+\lambda\|\textbf{b}\|_2}$$
where $$$\textbf{b}$$$ contains samples of the subpulse and $$$\textbf{A}$$$ is a system matrix of size $$$N_s\times N_t$$$, $$$ a_{ij}= S(\overrightarrow{x_i})e^{i\overrightarrow{x_i}\cdot\overrightarrow{k}(t_j)}$$$, N_s is the number of spatial locations, N_t is the number of time points, $$$S(\overrightarrow{x_i})$$$ is the measured B₁ amplitude at spatial location $$$\overrightarrow{x_i}$$$, $$$\overrightarrow{k}(t_j)$$$ is the excitation k-space trajectory traced out by the trapezoid gradient waveform, and $$$\lambda\|\textbf{b}\|_2$$$is a Tikhonov regularization term. The gradient direction is also optimized, and the subpulse duration is determined by spectral sampling requirements. Once the subpulse is designed, it is duplicated and weighted by a Gaussian or other spectral envelope.
Given a measured 3T cardiac B₁ map, an RF subpulse was computed with the following parameters: maximum duration = 250μs, maximum magnitude = 4G/cm, maximum slew rate = 14000G/cm/s, dwell time(dt) = 4µs, g_x = 0.22G/cm and g_y= 0.39G/cm. The subpulse was duplicated 145 times for a total pulse duration of 36ms. For comparison, a conventional 36 ms Gaussian pulse was also simulated. The pulses were scaled to a flip angle of 208°. The B₁ map was measured in vivo on a Siemens 3T scanner using a Turbo FLASH sequence proceeded by a 50° saturation pulse. Other B₁ mapping parameters were field of view (FOV) = 24.3×30cm², matrix = 156×192, slice thickness = 8mm, TE = 2.12ms, TR = 3.07s.
Numerical Simulations: Z-spectra were calculated by solving the Bloch-McConnell equations [5] using the ode45 function in MATLAB, for a two-pool model with a bulk water pool (Pool a) and a myocardial creatine pool (Pool b). The simulation parameters were: B₀ = 3T, T_1a = 2s , T_2a =120ms, Δω_a=0 ppm, T_1b =1.4s , T_2b =50ms , K_ba = 200Hz, Δω_b=1.8ppm and pool size ratio (b/a) f_b = 0.0018. Both pulses were repeated 25 times for saturation in the simulations, and the interpulse time delay was 21ms.

Results

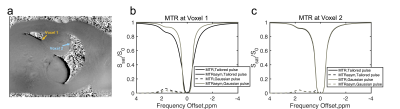
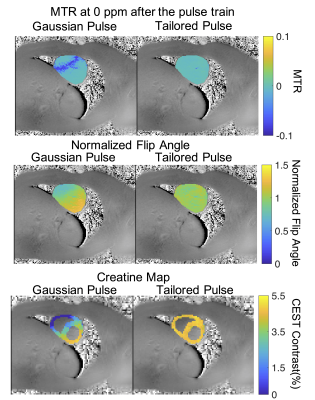
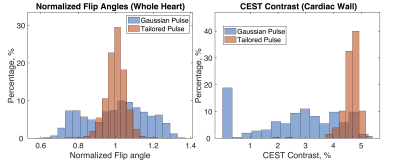
Figure 2 plots Z-spectra and MTRasym curves for two voxels at opposite edges of the heart, where Voxel 1 (orange arrow in Fig. 2a) has lower B₁ than prescribed, and Voxel 2 (blue arrow) experiences B₁ consistent with the prescribed flip angle. The effect of B₁ inhomogeneity with conventional Gaussian saturation manifests as reduced creatine CEST contrast and reduced full width half max of water saturation at Voxel 1 (Fig 2b) compared to Voxel 2 (Fig 2c). However, use of a tailored pulse train at Voxel 1 (Fig 2b) restores equal CEST saturation to that observed at Voxel 2 (Fig 2c), resulting in identical creatine CEST contrast.
The first row of Figure 3 shows that the tailored pulse train produces more uniform saturation at 0ppm across the heart: MTR = -0.0015±0.0036 (tailored) versus MTR = -0.0193±0.0247 (Gaussian). The second row shows normalized flip angle maps that demonstrate substantially enhanced spatial uniformity for the tailored pulse: the flip angle coefficients of variation were 0.05 (tailored) and 0.16 (Gaussian). The third row shows CEST contrast maps (%) of cardiac wall for each pulse. The CEST contrasts in the cardiac wall were 2.60±1.59% and 4.64±0.34% for the Gaussian and tailored pulses, respectively. Figure 4 shows normalized flip angle and CEST contrast histograms that illustrate the tighter distributions achieved with tailored saturation.

Discussion and Conclusion

In this work, we have designed and demonstrated a tailored spectral-spatial RF pulse with gradients which achieves a uniform saturation in the heart despite B₁ inhomogeneity, compared with a conventional Gaussian pulse. In this preliminary study, the tailored and Gaussian pulses were brought into a two-pool Bloch-McConnell model and the results showed the advantage of the tailored pulse. Future work will include an in vivo experiment and further multi-pool simulations fully validate the tailored pulses.
In conclusion, a tailored spectral-spatial RF pulse solved from a subject-specific B₁ map may lead to more uniform saturation in CEST imaging.

Acknowledgements

This work was supported by NIH grants R21 EB 024311, R01 EB 016695, R01 HL128592, and UH2 EB028908.