0486

Respiratory motion compensation for human cardiac 23Na MRI
Johanna Lott1,2, Armin M. Nagel1,3,4, Sebastian C. Niesporek1, Thoralf Niendorf5,6, Peter Bachert1,2, Mark E. Ladd1,2,7, and Tanja Platt1
1Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany, 2Faculty of Physics and Astronomy, University of Heidelberg, Heidelberg, Germany, 3Institute of Radiology, University Hospital Erlangen, Erlangen, Germany, 4Institute of Medical Physics, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 5Berlin Ultrahigh Field Facility (B.U.F.F.), Max Delbrueck Center for Molecular Medicine in the Helmholtz Association, Berlin, Germany, 6MRI. TOOLS GmbH, Berlin, Germany, 7Faculty of Medicine, University of Heidelberg, Heidelberg, Germany

Synopsis

Sodium (23Na) ion distribution plays a fundamental role in biological processes, in particular in myocardial function. 23Na MRI provides noninvasive information about the total tissue sodium concentration. However, short relaxation times, low signal-to-noise ratio, breathing and heart motion render quantitative cardiac 23Na MRI challenging and result in long acquisition times. We present a method to compensate for respiratory motion in 23Na MRI by adding a linear phase in k-space with the goal to determine myocardial tissue sodium concentration. This enables a reduced measurement time for quantitative cardiac 23Na MRI compared to retrospective sorting into one respiratory state.

Introduction

The tissue sodium (23Na) concentration (TSC) is associated with the viability of cells1, in particular in myocardial function2. In acute and chronic heart disease, alterations in myocardial sodium concentration have been observed with 23Na MRI3-5. In Conn’s Syndrome6 or after myocardial infarction7 the TSC is increased8 that indicates pathological changes. Thus, 23Na MRI may allow insights into the underlying mechanisms of sodium overload9. However, low spatial resolution, short relaxation times, and partial volume effects (PVE) render quantitative cardiac 23Na MRI challenging10. The previously applied retrospective sorting methods for cardiac11 and respiratory12 motion in 23Na cardiac MRI require long acquisition times and discard approximately 70% of the acquired projections10. Here, we present a method that shifts projections in k-space to compensate for respiratory motion aiming for clinically feasible acquisition times for myocardial sodium concentration assessment.

Methods

In vivo data of three healthy volunteers were acquired on a 7T MR system (Siemens, Erlangen, Germany) with an oval-shaped birdcage coil12 using a density-adapted 3D radial sampling scheme13 and golden angle projection distribution14. The following parameters were applied:TR=21ms, TE=0.97ms, α=61°, (∆x)3=(5mm)3, tAcquisition(ACQ)=35min. To determine binary masks, required for the correction of PVE, 1H measurements were conducted at 3T (navigator-gated (exhaled), ECG-triggered (diastole) Flash sequence15 TR=3ms, TE=1.3ms, α=20°, (∆x)3=(2mm)3 interpolated to (∆x)3=(1mm)3 , tACQ=6-10min).

To increase the number of projections used, all respiratory states within one cardiac phase (diastole) were considered: All projections are shifted to a reference state (end-exhaled) by adding a linear phase in k-space. The respiratory signal was normalized16 and equally divided into five states. The displacement Z in z-direction within a heart mask was determined using a linear fit of ∆Φ (=phase difference between the shifted and the reference state) in k-space center:
$$Z=\frac{\Delta \Phi }{2\cdot\Pi \cdot \frac{1}{2\cdot \Delta x}}$$
The data were processed in the following order and reconstructed using a NUFFT17 with Hanning filter: 1) correction for B1+ before any processing (Double-Angle-Method18, α=45°/90°, TR=150ms, TE=1.55ms, tACQ=12min35s, (∆x)3=(10mm)3); 2) sorting into cardiac state; 3) respiratory motion compensation; 4) B0 and 5) partial volume correction (PVC)10,19; 6) determination of myocardial TSC with binary masks and blood as reference. This evaluation was performed for datasets with a decreasing number of projections (full, half, quarter of tACQ). SNR was determined by NEMA Standards20.

Results

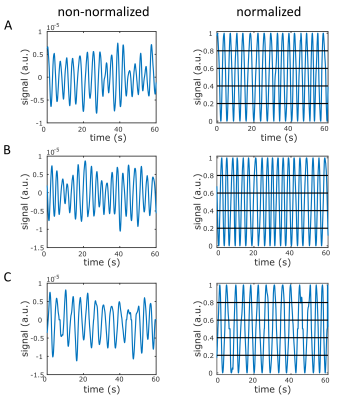
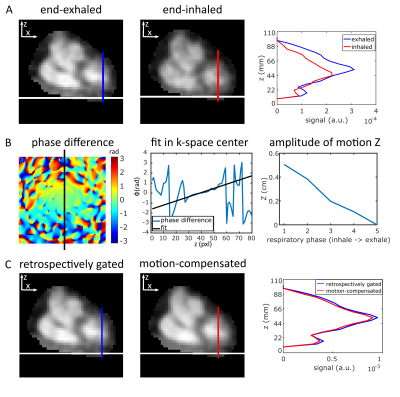
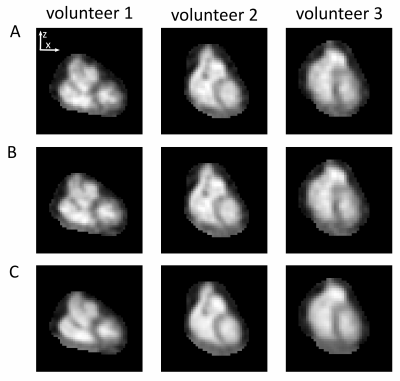
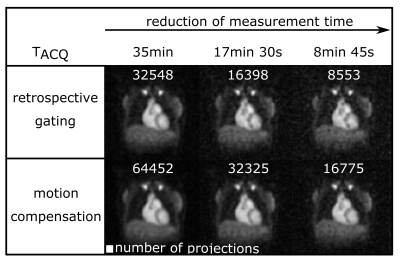
The respiratory signal was normalized and divided into five respiratory states, independent of the number of projections in each state (Fig.1).

Without motion compensation, the heart moves approximately (0.40±0.09)cm in z-direction (Fig.2A,3A) between the end-exhaled and end-inhaled state. The amplitude of this motion was ascertained for each respiratory state using a linear fit of the phase difference between each state and the reference state (Fig.2B). With motion compensation, respiratory motion is markedly reduced (Fig.2C,3B) and comparable to data with retrospectively sorted into the reference state (Fig.2C).

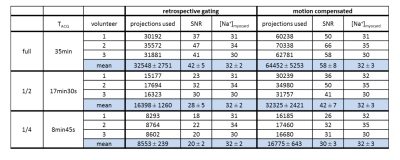
The number of projections used, SNR and myocardial TSC for reconstructions with and without motion compensation of the full, half and quarter dataset are shown in Table1. Applying retrospective gating uses about (49±0.29)% less projections for the reconstruction compared to the motion compensation approach. Hence, the SNR is reduced by a factor of (1.46±0.07) (approximately $$$\sqrt{\frac{100\%}{49\%}}\sim\sqrt{2}$$$, Fig.4). Despite decreased SNR and number of projections used, the determined myocardial TSC of (32±3)mM remains similar.

Discussion and Conclusion

With the presented motion compensation method, the respiratory movement of the heart in z-direction was detected and remarkably compensated. All projections obtained for the different respiratory states in one cardiac phase can be used for reconstruction and acquisition time can be reduced.

Due to the determination of the displacement Z by applying a linear fit in k-space, no reconstruction of subsets for an image registration in spatial domain is necessary21. Consequently, no minimal number of projections for subsets is required. The respiratory signal was equally divided into five states independent of the number of projections within one state.

At decreased SNR the determined myocardial TSC remains constant. A further reduction of the number of projections and thus of the measurement time could be feasible while still reaching similar values for myocardial TSC. Hence, a detailed analysis of the determined TSC and the arising variation due to an increasing noise level are required.

However, the approach has some limitations. To divide the respiratory signal into more than two states10, the respiratory signal was normalized. This assumes an equable respiration over the whole measurement time and might cause an overestimation or underestimation at some time points. In addition, the movement in x-/y-direction was not considered.

In conclusion, with the presented motion compensation, all projections of the different respiratory states that belong to the desired cardiac phase can be used for reconstruction. Consequently, measurement time can be reduced by a factor of two compared to retrospective gating into two respiratory states. The presented influence of noise using even smaller datasets demonstrates a consistently determined myocardial TSC. With the analyzed size of the dataset, measurement time could be reduced to <10min, which is suitable for a clinical assessment of myocardial sodium concentration. Our approach is not limited to the heart but can be also applied to MRI of e.g. the liver or abdomen.

Acknowledgements

This work was supported by iMed–the Helmholtz Initiative on Personalized Medicine.

References

1. Madelin G et al. Biomedical Applications of Sodium MRI in Vivo. J Magn Reson Imaging. 2013; 38(3): 511-529.

2. Sandstede JJ et al. Time Course of 23Na Signal Intensity after Myocardial Infarction in Humans. Magn Reson Med 2004; 52: 545-51.

3. Barclay JA et al. Electrolyte content of rat heart atria and ventricles. Circulation research 1960; 8: 1264-1267.

4. Constantinides CD et al. Noninvasive quantification of total sodium concentrations in acute reperfused myocardial infarction using 23Na MRI. Magn Reson Med 2001; 46 (6): 1144-1151.

5. Rochitte CE et al. Microvascular integrity and the time course of myocardial sodium accumulation after acute infarction. Circulation research 2000; 87(8): 648-655.

6. Christa M et al. Increased myocardial sodium signal intensity in Conn's syndrome detected by 23Na magnetic resonance imaging. Eur Heart J Cardiovasc Imaging. 2018; 30.3: 263-270.

7. Ouwerkerk R et al. Tissue sodium concentration in myocardial infarction in humans: a quantitative 23Na MR imaging study. Radiology. 2008; 248: 88–96.

8. Kim RJ et al. Relationship of elevated 23Na magnetic resonance image intensity to infarct size after acute reperfused myocardial infarction. Circulation. 1999; 100: 185-192

9. Aksentijevic D et al. Is there a causal link between intracellular Na elevation and metabolic remodelling in cardiac hypertrophy? Biochem Soc Trans. 2018; 46(4): 817-827.

10. Lott J et al. Corrections of myocardial tissue sodium concentration measurements in human cardiac 23Na MRI at 7 Tesla. Magn Reson Med. 2019; 82.1: 159-173.

11. Resetar et al. Retrospectively-gated CINE 23Na imaging of the heart at 7.0 Tesla using densityadapted 3D projection reconstruction. Magn Reson Imaging. 2015; 33(9): 1091-1097.

12. Platt T et al. In vivo self‐gated 23Na MRI at 7 T using an oval‐shaped body resonator. Magn Reson Med. 2018; 80: 1005–1019.

13. Nagel AM et al. Sodium MRI using a density‐adapted 3D radial acquisition technique. Magn Reson Med. 2009; 62: 1565–1573.

14. Chan RW et al. Temporal stability of adaptive 3D radial MRI using multidimensional golden means. Magn Reson Med. 2009; 61: 354–363.

15. Bi X et al. Whole‐heart coronary magnetic resonance angiography at 3 Tesla in 5 minutes with slow infusion of Gd‐BOPTA, a high‐relaxivity clinical contrast agent. Magn Reson Med. 2007; 58: 1–7.

16. Behl NG et al. Dynamic 23Na-Imaging of the human Lung with Fully Flexible Intrinsic Respiratory Gating. Proc Intl Soc Mag Reson Med. 2018; 26:0627.

17. Fessler JA et al. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans Signal Process. 2003; 51(2): 560-574.

18. Insko EK et al. Mapping of the Radiofrequency Field. J Magn Reson Ser A. 1993; 103(1): 82-85.

19. Niesporek SC et al. Partial volume correction for in vivo 23Na-MRI data of the human brain. NeuroImage. 2015; 112: 353-363.

20. Association NEM. NEMA Standards Publication MS 1-2001. 2001.

21. Weller DS et al., Motion-compensated reconstruction of magnetic resonance images from undersampled data. Magn Reson Med. 2019, 55: 36-45

Figures

Fig.1: Non-normalized (left) and normalized (right) respiratory signal of all volunteers (A: volunteer1, B: volunteer2, C: volunteer3) generated by a self-gating method12 directly from the 23Na MRI data. The normalized respiratory signal was divided into five respiratory phases (black lines).

Fig.2: Respiratory motion compensation for volunteer1 by shifting all projections to a reference state. A) The heart moves perpendicular to the white line in z-direction illustrated by the end-inhaled (phase 1) and end-exhaled (=reference, phase 5) state. B) In k-space the phase difference between the shifted and the reference image contains information about the displacement Z, which was determined for each respiratory state by a linear fit. C) The motion-compensated image shows the same sharp edges (line plots) as the reconstruction retrospectively gated into the exhaled phase.

Fig.3 (gif): The respiratory movement in z-direction (A) and the motion compensation approach (B) of the five respiratory phases is presented in a gif for all three volunteers. For each respiratory phase the projections were shifted by the determined displacement Z. After this shift, no motion is visible in the individual respiratory states (B). The respiratory motion-compensated images (C) contain all projections of the different respiratory states that belong to the desired cardiac phase.

Table1: Projections used, determined SNR and myocardial TSC of motion-compensated and retrospectively-gated reconstructions. Full, half and quarter sizes of the in-vivo 23Na MRI dataset were evaluated. According to the projections used, the SNR drops with $$$\sqrt{ratio\ of\ projections\ used}$$$.

Fig.4: Reconstructions of retrospective gating into the exhaled state and motion-compensated 23Na MRI data with reducing acquisition time from left to right (volunteer2). With a decreasing number of projections used (numbers given in white), the SNR declines. Motion compensation improves SNR compared to retrospective gating.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
0486