0465
MOCO-BUDA: motion-corrected blip-up/down acquisition with joint reconstruction for motion-robust and distortion-free diffusion MRI of brain1Center for Brain Imaging Science and Technology, Department of Biomedical Engineering, Zhejiang University, Hangzhou, China, 2Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, charlestown, MA, United States, 3Department of Radiology, Harvard Medical School, charlestown, MA, United States, 4State Key Laboratory of Modern Optical Instrumentation, College of Optical Science and Engineering, Zhejiang University, Hangzhou, China, 5Harvard-MIT Department of Health Sciences and Technology, Cambridge, MA, United States
Synopsis
We proposed a motion-correction method for joint reconstruction of blip-up/down EPI acquisition (BUDA-EPI) of brain diffusion MRI. Motion parameters were estimated and incorporated into the joint parallel imaging reconstruction of the blip-up/down multi-shot data, which included B0 field maps and Hankel structured low-rank constraint. The proposed motion-corrected reconstruction approach was demonstrated in vivo to provide motion-robust reconstruction of blip-up/down multi-shot EPI diffusion data.
Introduction
Diffusion MRI (dMRI) is commonly used in many clinical and neuroscientific studies. For fast dMRI, echo planar imaging (EPI) is widely used, however geometric distortion due to field inhomogeneity often degrades the image quality of EPI. To address this problem, FSL TOPUP1 is often used, where inverted phase-encodings, i.e blip-up and blip-down acquisitions are acquired separately and used to estimate the field map and perform distortion correction. Recently the BUDA-EPI approach2 was proposed, which performs blip-up and blip-down acquisitions with complementary k-space sampling (Figure 1A) along with joint parallel imaging reconstruction of these two acquisitions to boost SNR and mitigate artifacts at high accelerations.Motion artifacts pose a challenge in dMRI, as acquisitions are typically long and across a large number of diffusion directions3. In particular for BUDA-EPI, motion corruptions between the blip-up and –down shots result in poor B0 map estimation and image artifacts in the joint reconstruction (Figure 1C).
In this work, we introduce a motion-correction approach for BUDA-EPI reconstruction to achieve motion-robust distortion-free dMRI.
Method
Figure 1B shows the flowchart of the BUDA-EPI reconstruction approach. First, the blip-up EPI data and the blip-down EPI data were separately reconstructed using SENSE4 to obtain two images that were input to FSL TOPUP to estimate field maps. Along with the undersampled Fourier operator Ft and ESPIRiT5 sensitivity maps C, the estimated field maps Et were incorporated into the Hankel structured low-rank constrained ($$$\parallel H(b)\parallel_{*}$$$) joint reconstruction6-8 for both blip-up and -down data (dt), to obtain distortion-free images xt (for tth shots).To mitigate the motion artifacts shown in Figure 1C, we proposed a motion-correction reconstruction framework as shown in Figure 1D which utilizes the initial SENSE reconstructed images to estimate motion parameters and the field map (E0), as follows:
i.We assumed at the beginning of scan, the first pair of blip-up/down shots were acquired without motion, and regard this as our base reference position (POS0) from which a base field-map E0 was estimated using FSL TOPUP. (other blip-up/down pairs with no motion could also be used as reference)
ii.The method shown in Figure 2A was used to estimate the motion parameters of each EPI-shot separately compared to the base position using FSL MCFLIRT9. By iteratively using MCFLIRT incorporated with field-map (E0) information, a more accurate motion estimation was obtained with the distortion-corrected images.
iii.Motion parameters for each blip-up and each blip-down acquisition relative to the reference position were then incorporated into the motion transformation operator (Rt) to jointly reconstruct each blip-up and blip-down acquisition pair, to obtain a motion-corrected distortion-free image (Figure 1D).
The proposed method assumes that when motion occurs, the underlying B0-field inhomogeneity would approximately rotate with the motion. Figure 2B shows this to be a good approximation, where the rotated field map mimics closely that of the reacquired actual field map.
To test our proposed motion correction method, we designed static and dynamic experiments. For the static experiment, the volunteers first were required to keep still, this was regarded as a static reference. Then, the volunteers would move to another position and keep still during acquisition of all blip-up shots, and then move to the next position while acquiring the blip-down shots. For the dynamic experiment, the volunteers were asked to move indiscriminately after about 1 minute from the start of scan.
All studies were performed on a 3 Tesla MAGNETOM Prisma scanner with a 64-channel head receiver coil. For high-resolution in-plane correction experiments, the data were collected using: FOV=198×198×120mm3, 0.8×0.8×5mm3 resolution, Rinplane=4, partial-Fourier 6/8, TE/TR=67/3400ms, b-value=1000s/mm2 with 24 diffusion directions. For the isotropic 3D image correction experiments, imaging parameters were: FOV=204×204×90mm3, 1.5mm isotropic resolution, Rinplane×MB=4x2, partial-Fourier 6/8, TE/TR=55/3500ms.
Results
The performance of the proposed method at different motion levels was tested with the static experiment (as shown in Figure 3). BUDA-EPI reconstruction without motion-correction exhibited increasing levels of blurring and artifacts with increasing motion level (A to C), while the proposed motion-corrected reconstruction produced high-quality results in all cases, comparable to the reference images.Figure 4 shows the result of the dynamic experiment with high in-plane resolution and thick-slice, where 2D motion-correction was utilized. Figure 4A shows the time-varying motion estimates, with large translation and rotation up to +/-7mm and +/-15o. Corresponding reconstructed images of 4 timeframes with/without motion-correction are shown in Figure 4B respectively. Figure 4C shows the averaged DWI of the still motion-free period (first minute of scan) and the moving period (from first minute onward). The proposed method produced much improved averaged DWI, with some residual image blurring in this extreme motion case, likely due to significant spin-history related-artifacts.
Figure 5 shows the result of the static experiment of images in three orthonormal planes with 1.5-mm isotropic resolution and 3D motion-correction, with the estimated motion level shown at the top of the figure. The proposed method presented similar image quality compared to the reference images.
Discussion and Conclusion
We proposed a motion-correction reconstruction method for brain dMRI acquired with BUDA-EPI. In vivo results demonstrated the efficacy of our proposed method. Future work includes refinement of the motion estimation and incorporation of constrained reconstruction to mitigate the spin-history issue, which will further improve the performance of our technique.Acknowledgements
No acknowledgement found.References
1. Andersson JL, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage, 20(2), 870-888.
2. Liao C, Cao X, Cho J, Zhang Z, Setsompop K, Bilgic B. Highly efficient MRI through multi-shot echo planar imaging. Wavelets and Sparsity XVIII 11138, 2019.
3. Brown TT, Kuperman JM, Erhart M, White NS, Roddey JC, Shankaranarayanan A, Han ET, Rettmann D, Dale AM. Prospective motion correction of high-resolution magnetic resonance imaging data in children. Neuroimage 2010;53(1):139-145.
4. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magnetic Resonance in Medicine, 1999; 42(5), 952-962.
5. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, et al. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990-1001.
6. Low-Rank Modeling of Local k-Space Neighborhoods (LORAKS) for Constrained MRI. IEEE Transactions on Medical Imaging, 2014; 33(3): 668-681.
7. Mani M, Jacob M, Kelley D, Magnotta V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn Reson Med. 2017;78(2):494-507.
8. Shin PJ, Larson PE, Ohliger MA, Elad M, Pauly JM, Vigneron DB, et al. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med. 2014;72(4):959-70.
9.Jenkinson M, Bannister P, Brady JM and Smith SM. Improved Optimisation for the Robust and Accurate Linear Registration and Motion Correction of Brain Images. NeuroImage, 17(2), 825-841, 2002.
Figures
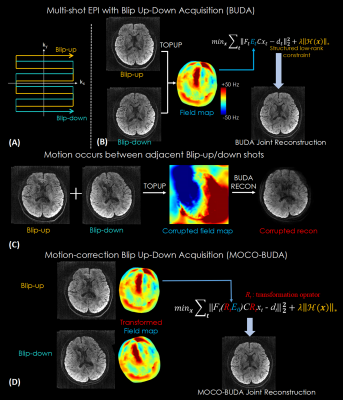
Figure 1.
(A) Flowchart of BUDA reconstruction. A Hankel structured low-rank constrained forward model is used to jointly reconstruct distortion-free images.
(B) A corrupted field map was estimated from TOPUP when motion occurred between blip-up/down shots, resulting in a corrupted image reconstruction.
(C) Flowchart of MOCO-BUDA reconstruction. The base field map E0 was transformed to fit position of shot, and images xt were corrected to the same base position across shots to enable the Hankel structured low-rank model, resulting in motion-corrected distortion-free images.
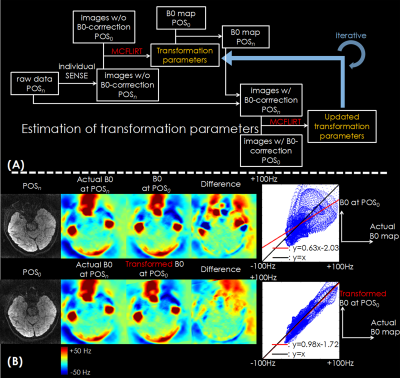
Figure 2.
(A) The flowchart of motion estimation based on MCFLIRT. Images from all shots are reconstructed separately with SENSE, and transformation parameters are found using MCFLIRT between shots. The transformation parameters are used to update the B0 map position, which is then used to correct the distortion. Updated images are used to find new transformation parameters, continuing iteratively to improve motion estimates.
(B) Using a transformed field map, the difference is much closer to the actual field map at POSn and the correlation between maps is close to unity.

Figure 3.
The reference no-motion acquisition (left), motion acquisition without correction (middle) and with motion-correction (right) images are compared with different levels of motion. For mild motion (top), the image without correction exhibited blurring and slight artifacts, while for moderate motion (middle), more distortion artifacts occurred. The artifacts in both cases could be recovered using the proposed method. When motion was significant (bottom), artifacts are severe, and the motion-corrected image is improved, yet still suffers from slight blurring.

Figure 4.
(A) Time-varying motion estimation of rotation and x/y-axis translation during a 24-direction DWI acquisition.
(B) Reconstructed images with/without motion correction of 4 respective time frames indicated by red boxes in (A).
(C) The averaged DWI of the motion-free period (directions 1-10) and moving period (directions 11~24).
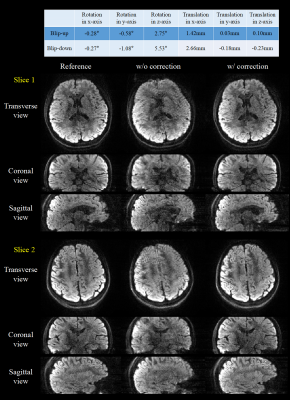
Figure 5.
Two slices in three orthorhombic views of the 1.5-mm isotropic resolution 3D images with/without motion correction. The 6-dimension motion parameters are shown in the top for both blip-up and –down shots.