Introduction

Radial acquisitions are inherently motion robust and repeated acquisition of the center of k-space provides an opportunity for estimation of motion from the data itself. Most self-navigation methods are based on detection of motion from the central k-space signal (self-encoded FID navigator), followed by co-registration of low-resolution images reconstructed from segments of radial spokes, to correct for periodic¹ or bulk motion². However, this requires a sufficient amount of data to be acquired in the same position to enable reconstruction of high-quality navigator images and there is a trade-off between tracking accuracy and frequency of motion updates, particularly for 3D imaging. Another problem is that gradient moment imbalances and magnetic field inhomogeneities lead to trajectory deviations that disrupt the self-navigator signal, as projections become off-centered³. In this work, we propose a novel motion compensation strategy that directly estimates motion parameters from self-encoded FID navigator signals in a 3D radial (kooshball) acquisition using a forward model that predicts the effects of both motion and magnetic field deviations on the self-navigator signal.

Methods

The self-encoded FID navigator signal from coil $$$j$$$ and spoke $$$n$$$ may be expressed as:
$$y_{j,n}(TE)=\int s_{j,n}(\mathbf{r})\cdotp{\rho}(\mathbf{r},TE)\cdotp{\exp}(i\gamma{TE}\delta B_{0,n}(\mathbf{r})) d\mathbf{r}$$
where $$$s_{j,n}(\bf{r})$$$ is the complex coil sensitivity profile at position $$$\bf{r}$$$ for object pose $$$n$$$; $$$\rho(\bf{r}, TE)$$$ is the effective proton density; and $$$\delta B_{0,n}(\bf{r})$$$ includes the effects of motion-induced magnetic field inhomogeneities, as well as gradient moment imbalances due to eddy current effects and residual gradient delays in each spoke. In the head frame of reference, these can modelled by low-spatial-order spherical harmonic (SH) expansion⁴.

Low-resolution (4 mm)³ Cartesian reference images with matched scan parameters were acquired on surface and body coils for estimation of $$$s_j$$$ and $$$\rho$$$. Motion of the coils relative to the object (6 DOF) and changes in SH coefficients up to second order were simulated to calibrate the FID motion model⁵. A gradient echo sequence was modified to acquire radial data with a pseudo-random 3D golden angle sampling pattern⁶. Three volunteers were scanned at 3T (MAGNETOM Skyra, Siemens Healthcare, Erlangen, Germany) with a 64-channel head coil, after providing written informed consent. Three scans were acquired for each volunteer using the above prototype radial sequence with 1) no motion; 2) abrupt head movements; and 3) continuous head shaking motion, with the following scan parameters: TE/TR = 4.57/10 ms, FA = 30°, FOV = 240 mm, 1-mm isotropic resolution, RBW = 400 Hz/pix, 48k spokes, total acquisition time 8 minutes. Isotropic gradient delay compensation was prospectively applied by adapting the readout dephasing gradient amplitude³. The central k-space signal was extracted from each spoke and phase-constrained least-squares fitting⁷ was used to estimate motion parameters from the complex FID signal every TR.

Rotations and translations were compensated retrospectively by phase-correcting and rotating each k-space line. Images were reconstructed in Matlab by applying an iteratively calculated weighting function⁸ and regridding the data using the NUFFT toolbox⁹. Quantitative image quality metrics (normalized root-mean-square error and structural similarity index) were computed relative to the corresponding no motion image. External electromagnetic (EM) tracking motion measurements (Robin Medical, Baltimore, MD) were also recorded for each and used to retrospectively correct the radial data for comparison.

Results

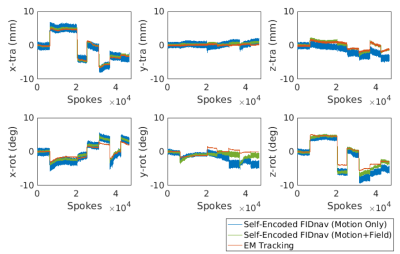
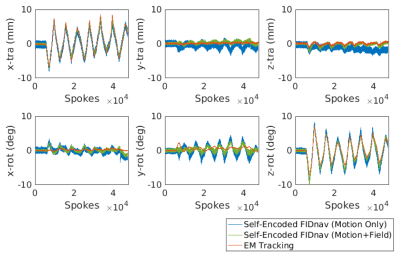
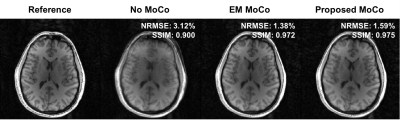
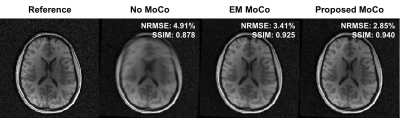
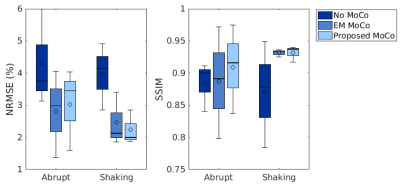
Figure 1 shows an example of motion measurements from self-encoded FID navigators (green) and external tracking (red) for abrupt head motion. The results of predicting motion without considering the effects of gradient field deviations on the self-encoded FID signals are also shown (blue). Results for continuous head shaking are shown in Figure 2. Across all volunteers and paradigms, self-encoded FID navigators had mean absolute errors of 0.68 ± 0.74 mm and 0.92 ± 0.80° relative to external tracking for maximum motion amplitudes of ~12 mm and 10°. Retrospective correction of the 3D radial data resulted in substantially improved image quality for both abrupt (Fig. 3) and continuous shaking motion (Fig. 4). NRMSE decreased from 4.13% ± 1.17% to 2.63 ± 0.97% following correction, while SSIM increased from 0.87 ± 0.06 to 0.92 ± 0.05 across all volunteers (Fig. 5).

Discussion

The proposed method enables quantitative tracking information to be rapidly obtained from self-encoded FID navigators in 3D radial MRI. Extending the FID navigator motion model to account for low-spatial-order field variations, which captures the effects of magnetic field inhomogeneities, residual gradient delays and eddy current effects, enables motion estimates with higher accuracy and precision compared to fitting for motion parameters alone. Mean absolute errors were within 10% of the maximum observed motion amplitude. Retrospective correction results are comparable to those achieved using external tracking, but without the need for any additional hardware. A key advantage of the proposed method is that it does not involve reconstruction and co-registration of navigator images, as such an approach assumes motion occurs intermittently with sufficiently long periods of motion-free time to construct navigator images. Instead, our approach obtains rigid-body motion estimates from every radial line, enabling much enhanced temporal resolution of motion measurement.

Conclusion

Quantitative motion parameters can be continuously measured from self-encoded FID navigator signals in each radial spoke using the proposed method, which has potential to compensate for fast, uncontrolled motion in children and other uncooperative subjects.

Acknowledgements

This research was supported in part by NIH grants R01 EB019483, R01 NS079788, R01 DK100404, R44 MH086984, IDDRC U54 HD090255, a pilot grant (PP-1905-34002) from National Multiple Sclerosis Society, and by an Early Career Award from the Thrasher Research Fund.