0391

  A Deep Learning Method for Sensitivity Enhancement in Deuterium Metabolic Imaging (DMI)
Siyuan Dong1, Henk M. De Feyter2, Monique A. Thomas2, Robin A. de Graaf3, and James S. Duncan4
1Department of Electrical Engineering, Yale University, New Haven, CT, United States, 2Department of Radiology and Biomedical Imaging, Yale University, School of Medicine, New Haven, CT, United States, 3Department of Radiology and Biomedical Imaging, Department of Biomedical Engineering, Yale University, School of Medicine, New Haven, CT, United States, 4Department of Radiology & Biomedical Imaging, Department of Electrical Engineering, Department of Statistics & Data Science, Yale University, New Haven, CT, United States

Synopsis

Deuterium Metabolic Imaging (DMI) is a novel approach providing 3D metabolic data from both animal models and human subjects. DMI relies on 2H MRSI in combination with administration of 2H-labeled substrates. Common to all MRI and MRSI methods, DMI's resolution is ultimately limited by the achievable SNR. This work proposes a data-driven method using a deep convolutional autoencoder to improve the SNR and increase the spatial resolution of DMI. The method was tested with simulated, phantom and in vivo experiments at various SNR levels to demonstrate its capability and precision for metabolic mapping using noisy DMI data.

Introduction

The recently proposed DMI is a non-invasive, easy-to-implement and robust metabolic imaging technique 1. However, acquiring high spatial resolution 2H NMR spectra is often limited due to low SNR inherent to the low metabolite concentrations. Several data processing methods have been proposed to deal with this problem for 1H MRSI techniques 2,3,4,5,6,7,8. 2H NMR spectra acquired following administration of [6,6-2H2]-glucose contain only up to 4 non-overlapping peaks. This relative simplicity makes DMI data a good candidate for a machine learning approach. We therefore combine deep learning with 2H MRSI data acquisition to increase the spatial resolution of DMI without compromising spectral quantification.

Methods

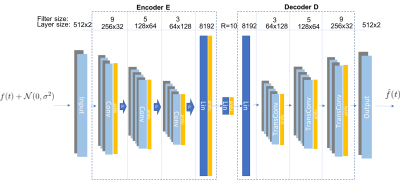
To increase spatial resolution of DMI we relied on a data-driven method using a common architecture in deep learning, autoencoder (AE), and a technique called transfer learning. AE is a type of neural network for learning efficient encodings of high-dimensional input data in an unsupervised manner. Specifically, it minimizes the mean-square-error loss function
$$L=||\mathbf{f}-D(E(\mathbf{f})))||_2$$
by finding the optimal parameterization of the encoder $$$E(\cdot)$$$ and the decoder $$$D(\cdot)$$$. Fig.1 shows the described architecture: a deep convolutional AE. The rationale is based on the notion that 1) compressing a noisy free induction decay (FID) $$$\mathbf{f}$$$ to a low-dimensional representation $$$E(\mathbf{f})$$$ removes insignificant features (noise) and that 2) features of the representation can be pre-determined from synthesized FIDs. The method consists of two steps: decoder-learning and representation-learning. In the decoder-learning step, AE is trained on a large number of synthesized noiseless FIDs (>10k, 80% training and 20% validation) which are generated through the standard FID specification
$$f(t)=\sum^M_{m=1}A_m exp(2\pi i(f_m+\delta f)t)exp(i\phi_m)exp(-\frac{t}{T_m})$$
where the chemical shifts $$$f_m$$$ come from prior knowledge, $$$\delta f$$$ models slight frequency shifts and $$$M$$$ denotes the expected number of distinct metabolites. Amplitudes $$$A_m$$$, lineshape parameters $$$T_m$$$, phases $$$\phi_m$$$ and $$$\delta f$$$ are each randomly generated from a uniform distribution over a reasonable range. After the training process, the decoder learns how to map from the low-dimensional representations to the noiseless FIDs. In the representation-learning step, the encoder is retrained (decoder frozen) on real DMI FIDs to find the representations that give the best reconstruction in terms of mean-squared-error. This is motivated by the idea of transfer learning where the model trained in one domain is used in another. A forward pass through the trained AE plus phase correction gives the final reconstruction. The decoder-learning step is only done once before it can be applied to different datasets with similar metabolic contents to execute the representation-learning step, which takes only ~2min for a 32x32x32 DMI dataset.
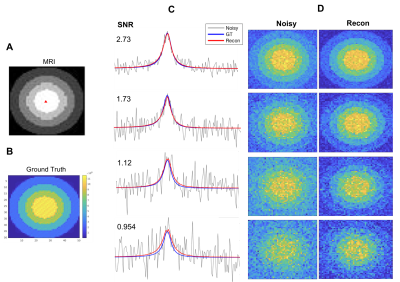
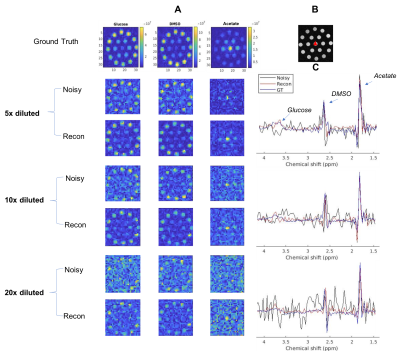
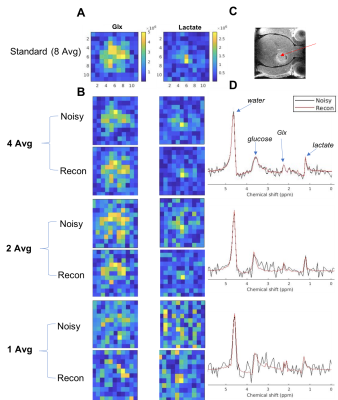
The algorithm's performance is demonstrated on simulated data, phantom data and in vivo data. The simulated experiment verifies the method on 2H NMR spectra containing a peak with Lorentzian lineshape. The phantom was constructed with multiple NMR tubes (Fig.4B) containing solutions of varying concentrations of 2H-labeled glucose, acetate and dimethyl sulfoxide (DMSO). The "ground truth" data were acquired in 1M solutions of the metabolites, and lower SNR DMI datasets were obtained by dilution. DMI data of brain glucose metabolism were acquired in vivo after administration of [6,6-2H2]-glucose in a Fischer 344 rat implanted with an RG2 brain tumor as described previously 1. The in vivo DMI data were acquired with 1 to 8 averages, to vary SNR levels.

Results and Discussion

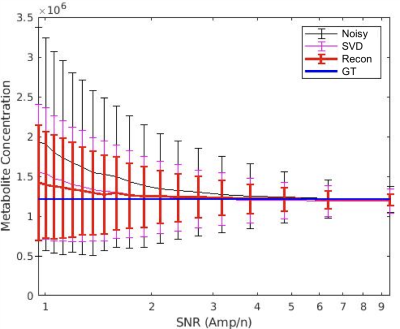
The performance of the algorithm on simulated data indicates that the reconstructed data approach the ground truth, and concentration maps are visually more diagnosable after reconstruction (Fig.2). The method improves the precision of the concentration measurement by 2 to 3 folds compared to the unprocessed data as illustrated by the standard deviation (SD) error bars in Fig.3. The SD of reconstructed data at SNR=2.5 is roughly that of unprocessed data at SNR=6.2. This implies that higher spatial resolution DMI datasets can be acquired (~1.4x higher in each direction) without a penalty in precision of the metabolite concentration estimates. Our newly described method also performed better than standard singular value decomposition (SVD) methods, a technique used in some aspects of previously described de-noising algorithms 2,6,7,8 (Fig. 3).
The algorithm also improved the appearance of phantom (Fig. 4) and in vivo DMI data (Fig. 5), showing that at least a 2-fold reduction in SNR can be tolerated. A slight reduction in performance is anticipated when using phantom and in vivo DMI data because of magnetic field inhomogeneity and multi-peak spectra phase correction.
In its current installation the described algorithm relies only on the known spectral information. The performance of the method is anticipated to improve further when spatial information is included, quantified magnetic field inhomogeneity (B0 map) is incorporated, and a more advanced learning methodology is designed.

Conclusion

A novel data-driven method using a deep convolutional autoencoder and transfer learning was implemented to improve the spatial resolution of DMI datasets while maintaining precision in determination of 2H-labeled metabolite concentrations. The algorithm-based reconstruction resulted in a 2-3 folds increase in SNR, which translates to a 40% increase in spatial resolution for DMI without any modification to hardware or data acquisition needed. The technique can be extended to other metabolic imaging techniques (1H MRSI) by synthesizing different training FIDs.

Acknowledgements

The research is supported by NIH grant R01EB025840, R01CA206180 and R01NS035193.

References

1. De Feyter, Henk M., Kevin L. Behar, Zachary A. Corbin, Robert K. Fulbright, Peter B. Brown, Scott McIntyre, Terence W. Nixon, Douglas L. Rothman, and Robin A. de Graaf. “Deuterium Metabolic Imaging (DMI) for MRI-Based 3D Mapping of Metabolism in Vivo.” Science Advances 4, no. 8 (August 2018): eaat7314. https://doi.org/10.1126/sciadv.aat7314.

2. Lam, Fan, and Zhi-Pei Liang. “A Subspace Approach to High-Resolution Spectroscopic Imaging: High-Resolution Spectroscopic Imaging.” Magnetic Resonance in Medicine 71, no. 4 (April 2014): 1349–57. https://doi.org/10.1002/mrm.25168.

3. Lam, Fan, Yudu Li, Rong Guo, Bryan Clifford, and Zhi‐Pei Liang. “Ultrafast Magnetic Resonance Spectroscopic Imaging Using SPICE with Learned Subspaces.” Magnetic Resonance in Medicine, September 4, 2019, mrm.27980. https://doi.org/10.1002/mrm.27980.

4. Lam, Fan, Yahang Li, and Xi Peng. “Constrained Magnetic Resonance Spectroscopic Imaging by Learning Nonlinear Low-Dimensional Models.” IEEE Transactions on Medical Imaging, 2019, 1–1. https://doi.org/10.1109/TMI.2019.2930586.

5. Gurbani, Saumya S., Sulaiman Sheriff, Andrew A. Maudsley, Hyunsuk Shim, and Lee A.D. Cooper. “Incorporation of a Spectral Model in a Convolutional Neural Network for Accelerated Spectral Fitting.” Magnetic Resonance in Medicine 81, no. 5 (May 2019): 3346–57. https://doi.org/10.1002/mrm.27641.

6. Brender, Jeffrey R., Shun Kishimoto, Hellmut Merkle, Galen Reed, Ralph E. Hurd, Albert P. Chen, Jan Henrik Ardenkjaer-Larsen, et al. “Dynamic Imaging of Glucose and Lactate Metabolism by 13C-MRS without Hyperpolarization.” Scientific Reports 9, no. 1 (December 2019): 3410. https://doi.org/10.1038/s41598-019-38981-1.

7. Nguyen, Hien M., Xi Peng, Minh N. Do, and Zhi-Pei Liang. “Denoising MR Spectroscopic Imaging Data With Low-Rank Approximations.” IEEE Transactions on Biomedical Engineering 60, no. 1 (January 2013): 78–89. https://doi.org/10.1109/TBME.2012.2223466.

8. Huang, Min, and Songtao Lu. “Application of SVD-Based Metabolite Quantification Methods in Magnetic Resonance Spectroscopic Imaging.” In Medical Imaging and Augmented Reality, edited by Guang-Zhong Yang, TianZi Jiang, Dinggang Shen, Lixu Gu, and Jie Yang, 4091:124–31. Berlin, Heidelberg: Springer Berlin Heidelberg, 2006. https://doi.org/10.1007/11812715_16.

Figures

Fig.1: Proposed architecture of deep convolutional autoencoder. Input consists of real and imaginary parts of FIDs (512 time points) in two channels. Conv, Lin, prelu, TransConv and P stand for convolution layer, linear layer, PRelu nonlinearity, transposed convolution layer and average (2) pooling. TransConv layers (with stride of 2) in the Decoder act as the inverse of corresponding Conv and P layers in the Encoder. The proper representation dimension R=10 was determined empirically. The input FIDs have small Gaussian noise added in each training epoch for model robustness.

Fig.2: 2D simulated data experiment with 10k synthesized FIDs and 50x50 DMI. The simulated DMI dataset contains a single peak with perfect lineshape, with stepwise increasing amplitudes towards the center. (A) Simulated 2D MRI; (B) Ground truth for metabolite concentration map (determined by peak integration on all pixels); (C) Noisy (unprocessed), reconstructed (~0.5min) and ground truth spectra from the pixel indicated with red triangle at four different SNR levels; (D) Comparisons of noisy and reconstructed metabolite concentration maps at corresponding SNR in (C).

Fig.3: Metabolite concentration vs. SNR for simulated data at the pixel in Fig.2A. Different SNR levels are generated by adjusting the SD of additive Gaussian noise. For each SNR level, the experiment is repeated 3000 times, from where mean (central lines) and SD (bars) are calculated. Blue, red, magenta and black curves show ground truth, reconstruction by present algorithm, reconstruction by traditional SVD method and the noisy data, respectively. Theoretically, the mean lines should coincide with the ground truth, although they are positively biased due to the phase correction.

Fig.4: 3D phantom experiment with 15k synthesized FIDs and 32x32x16 DMI dataset. (A) Concentration maps for glucose, DMSO and acetate before and after reconstruction (~2min). The metabolite concentrations are diluted 5x, 10x and 20x from the ground truth (1 mole) to generate different SNR levels. (B) One axial slice of the phantom MRI; (C) Noisy (unprocessed), reconstructed and ground truth spectra from the central test tube at corresponding levels of dilution in (A).

Fig.5: 3D in vivo rat experiment with 15k synthesized FIDs and 11x11x11 DMI dataset. (A) Concentration maps for DMI dataset of 16uL voxels, acquired with 8 averages. (B) Concentration maps for glutamate+glutamine (Glx) and lactate before and after reconstruction (~0.3min). The number of averages is reduced to generate different levels of SNR. (C) One coronal slice of the rat MRI with the tumor indicated by the red arrow. (D) Noisy and reconstructed spectra from a pixel in the tumor at corresponding number of averages in (B).

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
0391