Introduction

Dynamic ³¹P-MRS/MRSI is a promising tool for in vivo quantification of mitochondrial oxidative capacity in skeletal muscle by monitoring the depletion and recovery of the phosphocreatine (PCr) during stimulation-recovery experiments.^1-2 However, due to the inherently low SNR of ³¹P signal, dynamic ³¹P-MRSI experiments in rodent models are typically limited to low spatiotemporal resolution (≈1 cm³ per voxel, >30 sec/frame). This work is built upon our recent progress in accelerating dynamic ³¹P-MRSI using a low-rank tensor-based method.^3-4 We extended this method by learning the temporal priors with deep generative models and then incorporating them into the reconstruction via an information theoretical framework. Experimental results demonstrate that we can achieve high-resolution dynamic ³¹P-MRSI with 1.5×1.5×2 mm³ nominal spatial resolution and 5.1-sec temporal resolution in capturing the kinetics of metabolite changes in rat hindlimb during a stimulation-recovery protocol.

Method

Theory
The dynamic ³¹P-MRSI signal with $$$M$$$ molecules is expressed in terms of a tensor model as^3-4:
$$\hspace{16em}\rho(\boldsymbol{x},f,T)=\sum_{m=1}^M\rho_{m}(\boldsymbol{x},f,T)=\sum_{m=1}^M\sum_{\ell=1}^{L_m}\sum_{p=1}^{P_m}c_{m,\ell,p}(\boldsymbol{x})\varphi_{m,\ell}(f)\psi_{m,p}(T),\hspace{7em}(1)$$
where $$$\rho_m(\boldsymbol{x},f,T)$$$ is the image function for the $$$m$$$^th molecule, $$$\{\varphi_{m,\ell}(f)\}$$$ and $$$\{\psi_{m,p}(T) \}$$$ are the corresponding spectral and temporal basis functions which can be pre-determined from training datasets.
Eq. (1) is a rather general signal representation and often results in large estimation uncertainty in practice. In this work, additional SNR is gained by incorporating molecule-dependent temporal priors (denoted as $$$\{P_{\mathcal{g},m}\}$$$ ) into the signal model. These prior distributions are captured by deep generative models. The learned distributions are absorbed under the minimum cross-entropy principle by adding the following voxel-wise constraints into Eq. (1) (ignoring $$$\boldsymbol{x}$$$)^6-7:
$$\hspace{16em}\text{KL}\left(\int\left\lVert\rho_{m}(f,T)\right\rVert_2^2{df}\:\bigg\rVert\:{s}_{g,m}(T)\right)\leq\delta\hspace{16em}$$
$$\hspace{22em}\text{subj.}\:\text{to}\:s_{g,m}(T)\sim{P}_{\mathcal{g},m}, \hspace{19em}(2)$$
where $$$\text{KL}(\cdot\rVert\cdot)$$$ is the relative entropy and $$$s_{g,m}(T)$$$ represents samples drawn based on the learned distribution $$$P_{\mathcal{g},m}$$$ for the $$$m$$$^th molecule.

In Vivo Experiments
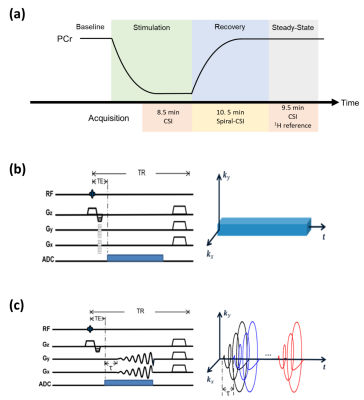
In vivo experiments were performed on three Sprague-Dawley rats on a 9.4T Bruker scanner. Each rat was anesthetized with isoflurane. Muscle contraction was induced by 2-Hz electrical stimulation via electrodes placed over the third lumbar vertebrae and the greater trochanter, leading to PCr depletion. Post-stimulation PCr recovery was captured by dynamic ³¹P-MRSI using a similar data acquisition scheme described previously (Fig. 1).⁴ Two spectral training datasets (matrix size: 8×8×6) were acquired before and after PCr recovery using 3D-CSI for adequate SNR in estimating $$$\{\varphi_{m,\ell}(f)\}$$$ . Dynamic imaging data (matrix size: 16×16×8) were acquired continuously for 10.5 min during the recovery period, using spiral trajectories for highly efficient coverage of data space. The TR/TE (160/0.69 ms) and FOV (24×24×16 mm³) were the same for both spectral training and imaging data. The temporal training datasets were experiment-independent and acquired in an existing depletion-recovery study that had similar molecular dynamics.⁸ Two rounds of stimulation-recovery experiments were conducted for each rat following the same data acquisition scheme.

Image Reconstruction
Molecular-dependent temporal prior $$$P_{\mathcal{g},m}$$$ was learned from the high-SNR training data using DCGAN (deep convolutional generative adversarial networks).⁵ The trained generative models can generate temporal functions for each molecule based on the prior distributions embedded in the training data.
The learned temporal priors were incorporated into reconstruction of the 5D dynamic ³¹P-MRSI using a two-step algorithm. First, initial reconstruction was generated by solving:
$$\hspace{16em}\{\bar{c}_{m,\ell,p}\}=\arg\min_{\{c_{m,\ell,p}\}}\left\lVert{d}-\mathcal{F}\left(\sum_{m=1}^M\sum_{\ell=1}^{L_{m}}\sum_{p=1}^{P_m}c_{m,\ell,p}(\boldsymbol{x})\varphi_{m,\ell}(f)\psi_{m,p}(T)\right)\right\rVert_2^2,\hspace{6.5em}(3)$$ where $$$d$$$ is the imaging data and $$$\mathcal{F}$$$ the imaging operator. The initial estimate of the temporal function was synthesized by: $$\hspace{16em}\bar{s}_m(\boldsymbol{x},T)=\int\left\lVert\sum_{\ell=1}^{L_m}\sum_{p=1}^{P_m}\bar{c}_{m,\ell,p}(\boldsymbol{x})\varphi_{m,\ell}(f)\psi_{m,p}(T)\right\rVert_2^2df.\hspace{12em}(4)$$
Second, we incorporated the learned temporal priors by imposing the constraints in Eq. (2), whose solution is (ignoring $$$\boldsymbol{x}$$$)^6-7:
$$\hspace{16em}\min_{s_{g,m}\sim{P}_{\mathcal{g},m},\{c_{n}\}}\left\lVert{s}_m(T)-s_{g,m}(T)\sum_{n}c_{n}e^{i2\pi{n}\Delta{F}T}\right\rVert_2^2,\hspace{14.5em}(5)$$
where $$$\Delta{F}$$$ is the spectral resolution corresponding to $$$T$$$ . In practice, since the probability density function $$${P}_{\mathcal{g},m}$$$ is often intractable, we actively generated the random sample $$$s_{g,m}(T)\sim{P}_{\mathcal{g},m}$$$ and solved Eq. (5) until $$$\text{KL}(s_{g,m}(T)\sum_{n}c_{n}e^{i2\pi{n}\Delta{F}T}\:\rVert\:s_{g,m}(T))\leq\delta$$$ .

Results

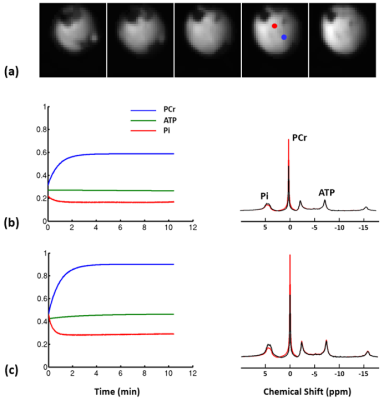
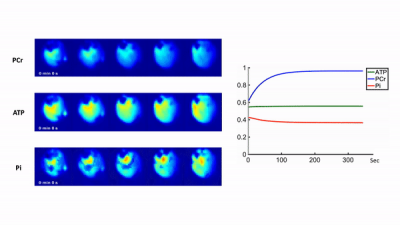
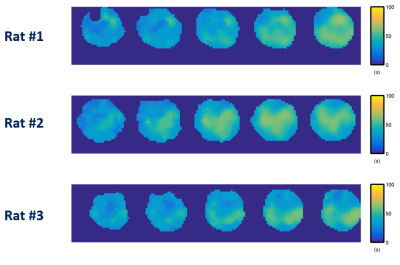
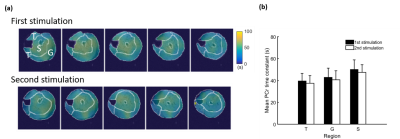
Representative ³¹P spectra and the time courses of metabolite changes after stimulation from our reconstructed data are shown in Fig. 2. Figure 3 shows a movie of concentration dynamics of PCr, ATP, and Pi during the recovery process. The time constant of PCr recovery, an index of mitochondrial oxidative capacity, was estimated by fitting the PCr concentration dynamics to an exponential function. Figure 4 shows the time constant maps from three different rats obtained by the proposed method. The time constant of PCr recovery in different muscle types was quantified by segmenting the muscle into the tibialis anterior and posterior, gastrocnemius, and soleus and plantaris (Fig. 5). Tibialis anterior and posterior muscle showed relatively faster PCr recovery with a shorter time-constant (37.9±1.42 sec) comparing to gastrocnemius (45.5±2.93 sec) and soleus and plantaris (47.7±3.57 sec). Interestingly, PCr recovery rate in the second stimulation was slightly faster than the first stimulation.

Conclusions

In the current study, temporal priors were learned using deep generative models and incorporated into the MRSI reconstruction to enable high-resolution 5D dynamic ³¹P-MRSI for quantification of PCr recovery kinetics during stimulation-recovery experiments in popular rodent models. The regional differences observed in the current study may be attributed to the composition of different muscle fiber types with distinct metabolic profiles.^9-10 Further, the slight acceleration of PCr recovery kinetics after the second stimulation might suggest an acute response to the first stimulation.

Acknowledgements

This work reported in this paper was supported, in part, by the following research grants: NIH-R21-EB023413, NIH-R01-EB023704, and NIH-U01-EB026978.