0388

High Resolution MR Spectroscopic Imaging Using Deep Image Prior Constrained Subspace Modeling

Kuang Gong¹, Paul Kyu Han¹, Thibault Marin¹, Georges El Fakhri¹, Quanzheng Li¹, and Chao Ma¹
¹Gordon Center for Medical Imaging, Department of Radiology, Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States

Synopsis

The subspace-based method, known as SPICE, is an emerging technique that achieves rapid high-resolution MRSI with good SNR. In SPICE, the spectrum at each voxel is represented as a low-dimensional subspace or manifold, where the basis functions or features are learned from training data. The spatial coefficients of the subspace model are estimated by fitting the model to the k-space data for image reconstruction. In this work, we propose to extend the SPICE framework by representing the spatial coefficients of the subspace model using deep image prior for improved image reconstruction.

Introduction

Clinical applications of MR Spectroscopic Imaging (MRSI) have been limited by low SNR and poor resolution. Many constrained image reconstruction methods have been proposed to address these issues, including methods exploiting sparsity constraints¹, spectral prior information², anatomical prior information³, and low-rank constraints^4-6. The subspace-based method, known as SPICE, is an emerging technique that achieves rapid high-resolution MRSI with good SNR^7-12. In SPICE, the spectrum at each voxel is represented as a low-dimensional subspace^7,13 or manifold¹⁴, where the basis functions or features are learned from training data. The spatial coefficients of the subspace model are estimated by fitting the model to the k-space data (often with edge-preserving regularizations³) for image reconstruction^8-12. In this work, we propose to extend the SPICE framework by exploring non-linear representations of the spatial coefficients of the subspace model for improved image reconstruction. More specifically, we use the deep image prior (DIP) framework^15-17 to represent the spatial coefficients of the subspace model as outputs of a convolutional neural network (CNN) with anatomical prior images as the input. One noticeable feature of our method is that the network can be trained only using the noise-corrupted and sparsely sampled k-space data. This is an important advantage over the supervised learning-based methods^18-27 because high-quality training labels (i.e., high-resolution and high-SNR MRSI data) are challenging to obtain for in vivo MRSI. We demonstrate the effectiveness of the proposed method using simulation, phantom and in vivo studies.

Theory

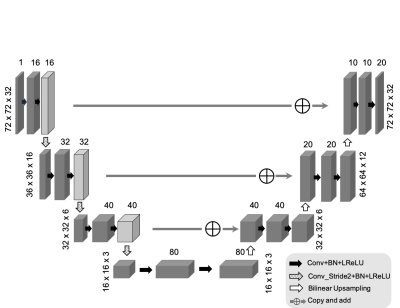
In SPICE, the MRSI image is modeled as partially separable functions:$$$I(x,t) = \sum_l u_l(x) v_l(t),$$$ where $$$V=\{v_l(t)\}_l$$$ are the temporal basis functions and $$$U=\{u_l(x)\}_l$$$ are the corresponding spatial coefficients. While $$$V$$$ can be predetermined from training data and the physical model of metabolite spectrum, the spatial basis $$$U$$$ is the only unknown, which is estimated by fitting the model to the k-space data. Edge-preserving regularizations³ are often used for improved image reconstruction^8-12.

Figure 1 shows the diagram of the proposed method. We propose to represent the spatial coefficients $$$U$$$ by a CNN output: $$$U = f(\theta|z)$$$, where $$$f:\mathbb{R}\rightarrow\mathbb{R}, \theta, z$$$ indicate the CNN, network trainable parameters and anatomical prior image (as network input), respectively. Note that the real and imaginary part of $$$U$$$ are treated as separate output channels of the CNN. A modified 3D U-net shown in Fig. 2 is used as the network structure²⁸. The image reconstruction problem can be reformulated as the following network training problem:$$\theta^* =\underset{\theta}{\operatorname{argmin}} ||\Omega FS\{f(\theta | z)V\}- d||_2^2, (1)$$ where $$$\Omega, F, S, d$$$ denotes down-sampling mask, Fourier transform, coil sensitivity maps, and k-space data, respectively. Note that the k-space data rather than high-quality training labels are used for training.

As the system matrix is coupled with the neural network, solving the optimization problem in (1) directly can be computationally inefficient. We use the alternating direction method of multipliers (ADMM) method²⁹ to decouple the optimization problem into the following three subproblems,$$U^{n+1}=\underset{U}{\operatorname{argmin}}||\Omega FS\{UV\} - d||_2^2 + \frac{\rho}{2} \Vert U - f({\theta}^n|z) + {\mu}^n\Vert_2^2, (2) $$$${\theta}^{n+1}=\underset{\theta}{\operatorname{argmin}}\Vert f(\theta|z)- ({U}^{n+1} + {\mu}^n)\Vert_2^2, (3)$$$${\mu}^{n+1} ={\mu}^n + U^{n+1} - f({\theta}^{n+1}|z). (4)$$ The subproblem in (2) is a conventional SPICE reconstruction with $$$l_2$$$-norm regularization, where $$$f({\theta}^n|z) - {\mu}^n$$$ can be considered as prior knowledge of $$$U$$$. The subproblem in (3) is a standard network training problem, which is solved using the L-BFGS algorithm³⁰ due to its monotonic property. For each loop the network training step was run 20 epochs and in total 100 outer-iterations were run.

Results

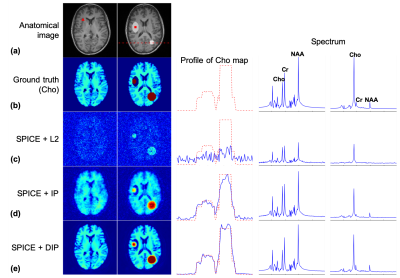
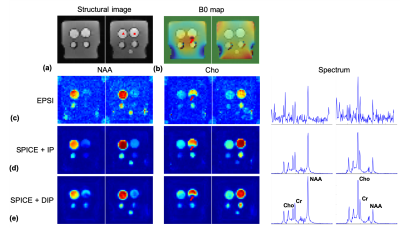
A simulation phantom was generated using in vivo MPRAGE images. Metabolite spectra were assigned to gray and white matter based on literature values. Artificial lesions were inserted to the MPRAGE images and metabolite maps but with different boundaries. Figure 3 shows the MRSI signals reconstructed from noise corrupted k-space data (96x96x32x640 spatiospectral encodings) using the SPICE method with $$$l$$$2-norm regularization, anatomical image prior³, and deep image prior constraints, respectively. The proposed method produced significantly improved MRSI images over the compared methods. Note that the proposed method better recovered the inserted lesions than the compared methods even when the boundaries shown in the anatomical prior image do not match with the true boundaries of the metabolite maps.

Phantom experiments were performed on a 3T Siemens Prisma scanner to further validate the proposed method. EPSI data were acquired with TR/TE=410/4.5ms and 72x72x32x330 spatiospectral encodings (0.88 ms echospacing). Additional low-resolution CSI data (16x16 spatial encodings) were acquired to estimate the temporal basis function for SPICE based reconstructions. Representative reconstruction results are shown in Fig. 4. The proposed method produced MRSI images of the best quality over the compared methods.

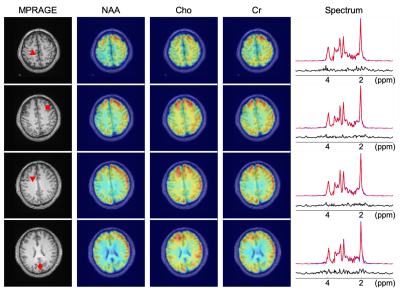
The feasibility of the proposed method to in vivo MRSI was tested using MRSI data acquired from a healthy volunteer (approved by our local IRB) with the same imaging parameters as the phantom experiment. Representative metabolite maps and spectra are demonstrated in Fig. 5, showing encouraging image and spectrum quality.

Conclusion

We have presented a novel reconstruction framework for high-resolution MRSI by using deep image prior constrained subspace modeling. Results of computer simulations along with phantom and in vivo experiments demonstrate the effectiveness of the proposed method.

Acknowledgements

This work was supported in part by NIH grants P41 EB022544, R01 CA165221, R01 AG052653, and T32 EB013180.

References

1. Laruelo A. et al., Hybrid sparse regularization for magnetic resonance spectroscopy. in Proc. IEEE EMBC, 2013, pp. 6768-6771.

2. Eslami R and Jacob M, Robust reconstruction of MRSI data using a sparse spectral model and high resolution MRI priors, IEEE Trans. Med. Imaging, 2010;29:1297-1309.

3. Haldar JP.et al., Anatomically constrained reconstruction from noisy data. Magn. Reson. Med., 2008;59:810-818.

4. Kasten J, et al., Data-driven MRSI spectral localization via low-rank component analysis. IEEE Trans. Med. Imaging, 2013;32:1853-1863.

5. Nguyen HM, et al., Denoising MR spectroscopic imaging data with low-rank approximations. IEEE Trans. Biomed. Eng., 2013;60:78-89.

6. Yan Liu, et al., Improved Low-Rank Filtering of Magnetic Resonance Spectroscopic Imaging Data Corrupted by Noise and B0 Field Inhomogeneity. IEEE Trans. Biomed. Engineering, 2016;63:841-849.

7. Lam F and Liang ZP. A subspace approach to high-resolution spectroscopic imaging. Magn. Reson. Med. 2014;71:1349-1357.

8. Lam F, et al. High-resolution 1H-MRSI of the brain using SPICE: Data acquisition and image reconstruction. Magn. Reson. Med. 2016;76:1059-1070.

9. Ma C, et al. High-resolution 1H-MRSI of the brain using short-TE SPICE. Magn. Reson. Med. 2017;77:467-479.

10. Ma C, et al. High-Resolution Dynamic 31P-MRSI Using a Low-Rank Tensor Model. Magn. Reson. Med. 2017;78:419-428.

11. Peng X, et al. Simultaneous QSM and metabolic imaging of the brain using SPICE. Magn. Reson. Med. 2018;79:13-21.

12. Guo R, et al., Simultaneous metabolic and functional imaging of the brain using SPICE, Magn. Reson. Med. 2019;82:1993-2002.

13. Lam F, et al., Ultrafast magnetic resonance spectroscopic imaging using SPICE with learned subspaces, Magn. Reson. Med. 2020;83:377-390.

14. Lam F, et al., Constrained Magnetic Resonance Spectroscopic Imaging by Learning Nonlinear Low-DimensionalModels, IEEE Trans. Medical Imaging, 10.1109/TMI.2019.2930586.

15. Ulyanov D, et al., Deep image prior. arXiv preprint arXiv:1711.10925. 2017 Nov 29.

16. Gong K, et al., PET image reconstruction using deep image prior. IEEE Trans. Med. Imaging, 2019;38:1655-1665.

17. Gong K, et al., Arterial Spin Labeling MR Image Denoising and Reconstruction Using Unsupervised Deep Learning. NMR in Biomed, in press.

18. Wang S, et al. Accelerating magnetic resonance imaging via deep learning. In Proc. IEEE ISBI, 2016, pp. 514-517.

19. Sun J, et al.. Deep ADMM-Net for compressive sensing MRI. In Advances in Neural Information Processing Systems 2016, pp. 10-18.

20. Schlemper J, et al.. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Trans. Medical Imaging. 2018;37:491-503.

21 Hammernik K, et al., Learning a variational network for reconstruction of accelerated MRI data. Magn. Reson. Med.. 2018;79:3055-71.

22 Zhu B, et al., Image reconstruction by domain-transform manifold learning. Nature. 2018;555(7697):487.

23 Mardani M, et al., Deep generative adversarial networks for compressed sensing automates MRI. arXiv preprint arXiv:1706.00051. 2017

24 Aggarwal HK, et al., MoDL: Model Based Deep Learning Architecture for Inverse Problems. IEEE Trans. Med. Imaging. 2018 Aug 13.

25. Han Y, et al., Deep learning with domain adaptation for accelerated projection‐reconstruction MR. Magn. Reson. Med.. 2018;80:1189-205.

26. Yang G, et al., Dagan: Deep de-aliasing generative adversarial networks for fast compressed sensing mri reconstruction. IEEE Trans. Med. Imaging. 2018;37:1310-21.

27. Qin C, et al., Convolutional recurrent neural networks for dynamic MR image reconstruction. IEEE Trans. Med. Imaging. 2018.

28. Ronneberger O, et al., U-net: Convolutional networks for biomedical image segmentation. arXiv:1505.04597. 2015, May 18.

29. Boyd S, et al., Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine learning. 2011;3:1-22.

30. Zhu C, et al., Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Transactions on Mathematical Software (TOMS). 1997 Dec 1;23(4):550-60.

Figures

Figure 1. Diagram of the proposed framework for high-resolution MRSI reconstruction. The structure of 3D-Unet is shown in Figure 2.

Figure 2. The schematic plot of the modified 3D Unet structure used in this work. The spatial input size for each layer is based on the MRSI image size. The network input is the magnitude of anatomical reference image, and the network output has two channels: real and imaginary parts of the U image. Here the rank is 10 and the final output channel number is 20.

Figure 3. Simulation results: (a) Anatomical reference image. (b) Ground truth MRSI signal. (c) to (e) MRSI signals reconstructed using SPICE with L2-norm regularization, image prior, and deep image prior constraints, respectively. The middle column show the profiles of the reconstructed Cho map along the red-dash line in (a). The right columns show spectra from the voxels marked by the triangle and square in (a). The proposed method produced improved MRSI images over the compared methods.

Figure 4. Phantom results. Compared to the Fourier construction in (c), SPICE based reconstructions in (d) and (e) show less artifacts (residual water signal) and significantly improved SNR. There was signal loss in one tube due to B0 inhomogeneity and aggressive water removal (arrow in c), resulting in mismatch between the structural image and metabolite maps. The proposed method better preserved the edges of the metabolite signals in this region than the conventional SPICE reconstruction.

Figure 5 In vivo results obtained by the proposed method using MRSI data acquired from a healthy volunteer. The metabolites from representative slices are shown with overlaid anatomical structural images. The last column on the right shows representative spectra from voxels in the gray and white matter as marked in the structural images. The reconstructed spectra (blue lines) were fitted using the QUEST method (red lines) with residuals shown as black lines.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

0388