Introduction

Balanced Steady State Free Precession (bSSFP) has recently attracted increased interest for electric properties tomography (EPT) of the brain and the lung^1,2. To this end, the phase of bSSFP is used, yielding an estimate of the transceive phase under ideal conditions that is at on-resonance and in the limit of TR << T₂. On the one hand, a method to address this issue was proposed by Ozdemir et al.² by the acquisition of two phase-cycled bSSFP scans, a B₀ map and a T₂ map. On the other hand, it was shown that relaxometry can be performed using the SSFP modes retrieved from multiple phase-cycled bSSFP scans³. In this work, we thus explore the potential to perform EPT in conjunction with tissue relaxometry from a set of multiple phase-cycled bSSFP scans.

Methods

Sampling the frequency response profile of bSSFP from multiple scans with different RF phase increments provides an elegant way to access the SSFP configuration modes, as described in a seminal work by Zur⁴. In principle, the signal $$$S$$$ contains the information about the configurational states $$$M^{(n)}$$$ and the RF transmit phase $$$\varphi^+$$$:

$$ S(x\cdot TR) \propto E_2^x e^{i\varphi} e^{ix\vartheta} \sum_{n=-\infty}^{\infty} e^{in\vartheta}M^{(n)} \approx E_2^x e^{2i\varphi^+} e^{ix\vartheta} \sum_{n=-\infty}^{\infty} e^{in\vartheta}M^{(n)}\quad , \tag{1} $$

where we used the transceive phase assumption, $$$ 2\varphi^+\approx\varphi $$$ (with $$$\varphi$$$ being the transceive phase), and $$$\vartheta$$$ denotes the phase which is accumulated during one repetition time (TR) interval as a consequence of the static field inhomogeneity (as usual, $$$ E_{2}^{x} \triangleq e^{-x\cdot TR/T_2} $$$, and diffusion and finite RF pulse effects are neglected). It is now directly evident (cf. Eq. (1)), that the transmit phase can be retrieved, e.g. from a measurement of the two lowest order configuration modes ($$$F_{-1},\;F_{0}$$$) for a centered echo (i.e., $$$x$$$ = 1/2):
$$ \varphi^+=\frac{arg[\frac{1}{2}(F_{-1}\cdot F_{0})]}{2} \quad , \tag{2} $$
where
$$ F_{-1}\sim e^{2i\varphi^+}e^{-i\vartheta/2}M^{(-1)},\quad F_{0}\sim e^{2i\varphi^+}e^{i\vartheta/2}M^{(0)} \quad . \tag{3}$$
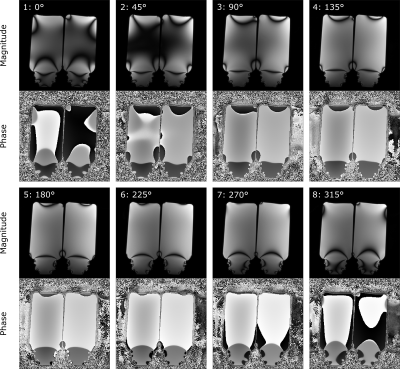
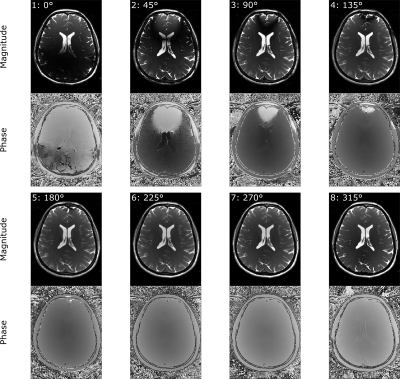
In this work, eight phase-cycled 3D bSSFP scans were acquired with RF phase increments of 0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°. Other sequence parameters were: TR/TE = 5.0 ms / 2.5 ms, 1.3 mm isotropic voxel size, 295 Hz/px bandwidth and 192x192x128 matrix size for the phantom, 305 Hz/px and 192x168x128 for in-vivo, non-selective excitation with 30° flip angle. A single bSSFP scan took 123 s for the phantom, 107 s for the in-vivo brain scan. Experiments were carried out on a 3T clinical MR system using a 20 channel head coil for reception. Two saline phantoms were prepared with 2 g/L and 8.8 g/L sodium chloride yielding an estimated electrical conductivity of 0.34 S/m and 1.39 S/m respectively⁵. MnCl was added (0.125 mM) to reduce the relaxation times to tissue comparable values (T₁$$$\sim$$$870 ms,T₂$$$\sim$$$ 70 ms). The conductivity was reconstructed from the estimated transmit phase by following relation:
$$ \sigma\approx\frac{1}{\mu_{0}\omega}\triangledown^2\varphi^+ \quad . \tag{4}$$
A weighted numerical differentiation was performed to adjust for tissue boundaries⁶. For the phantom, the phase as well as the conductivity were smoothed by applying a gaussian shaped low pass filter. Due to additional complexity of in vivo data, the phase was filtered using a median filter with an isotropic kernel size of 7 and subsequent edge-preserving Gaussian bilateral filtering. The obtained conductivity was subject to gaussian filtering.

Results

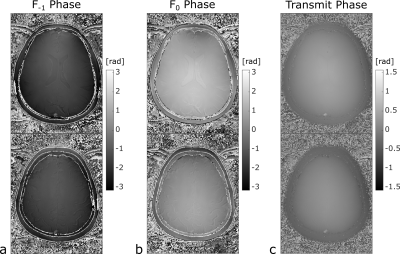
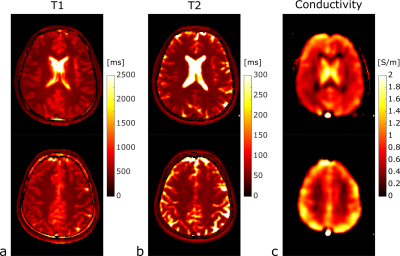
Exemplary images from the eight phase-cycled bSSFP scans are shown in Fig. 1 (phantoms) and in Fig. 2 (in vivo), respectively. Using Zur’s approach to retrieve the lowest configurational modes $$$F_{-1}$$$ and $$$F_{0}$$$, and thus the transmit phase using Eq. (2), the conductivity can be estimated (Fig. 3). For the phantoms, an average conductivity of 1.46±0.18 S/m for the left and 0.40±0.08 S/m for the right phantom was obtained; in very good agreement with the theoretical expectations. For the in-vivo brain scans, the retrieved phase of the two lowest configurational states, together with the reconstructed transmit phase are shown for two different axial slice positions in Fig. 4. Generally, accessing the modes allows to retrieve the tissue relaxivities (T₁, T₂), as well as the conductivity, as demonstrated for the same slice positions in Fig. 5. Typical conductivity values for white matter, gray matter and cerebrospinal fluid are about 0.32 S/m, 0.65 S/m and 1.84 S/m respectively.

Discussion and Conclusion

The intrinsic properties of bSSFP, that is rapid imaging with high signal-to-noise, makes this method highly interesting for EPT, but confounding factors, such as field inhomogeneities and transverse relaxation, needs to be accounted for. In this work, we have shown that the transmit phase and thus the conductivity can be successfully estimated from a set of phase-cycled bSSFP scans, recently suggested for tissue relaxometry³. The validity of the proposed methodology was confirmed in phantoms and the feasibility was demonstrated for conductivity mapping of the brain in vivo. In conclusion, we have suggested to exploit the SSFP configuration space, retrieved from multiple phase-cycled bSSFP scans, not only for relaxometry but in conjunction with electrical conductivity mapping. Requiring no additional scan time, this approach has the potential for clinical translation and application of EPT.

Acknowledgements

This work was supported by the Swiss National Science Foundation (SNF grant No. 325230_182008).