Introduction

MRE is conventionally performed by the application of oscillating motion encoding gradients (MEG) that are able to encode the spins motion oscillating at a given frequency into the NMR signal phase¹. Usually, several periods of MEG are needed to increase the phase encoding but this results in a long echo time and thus a degraded SNR. A new encoding strategy of the shear wave propagation, by simultaneously applying an Optimal Control (OC) RF pulse and a constant gradient was already demonstrated² when optimized pulses were applied in a conventional RARE MRE sequence, achieving echo times of about 10ms. In order to further reduce the TE, we propose to create a radial acquisition MRE sequence. For this purpose, a UTE sequence was adapted by adding specifically designed OC RF pulses.

Methods

Optimal control theory was applied to MRE to design the optimized RF pulses. The computation is performed with the GRAPE algorithm³. As we know that the macroscopic magnetization $$$\vec{M}$$$ is governed by Bloch equations, the OC algorithm provides the RF control parameter to apply in order to manipulate the isochromats from the steady state towards a desired target state.
The RF pulse is simultaneously applied with a constant gradient $$$G$$$ to perform slice selectivity⁴ while a shear wave motion at frequency $$$f_e$$$ produces static field variations given by $$$\Delta B_{0}^{(i,j)}(t)=G(Asin(-2πf_et+θ^{(i)})+z^{(j)})$$$, where $$$z^{(j)}$$$ represents the isochromat (i,j) location in the slice (Figure 1). Finally, different target states are attributed whether the considered isochromat is located in the passband ($$$Δ_{in}$$$) or in the stopband ($$$Δ_{out}$$$). The isochromats phase is directly linked to the phase of the wave motion they are experiencing⁵:
$$\vec{T}^{(i,j)}=\rho(cosΦ^i,sinΦ^i,0)\: if \:j\in Δz_{in}$$ $$\vec{T}^{(i,j)}=\rho(0,0,1)\: if \:j\in Δz_{out}$$
A UTE readout was experimentally compared to a Turbo Spin Echo using the same OC RF pulse and a conventional MRE using a similar Turbo Spin Echo through phantom MRE experiments. For this purpose, a UTE sequence was modified by adding the optimized pulses dedicated to MRE. Radial acquisitions trajectories starting in the out-center of the k space were used.
All the experiments were carried on an agar phantom doped with NiSO4 (0.2% NiSO4, 3.8% agar) with [T1,T2]=[230,45]ms. A piezoelectric actuator (CEDRAT Technologies) was used as mechanical transducer for motion generation.
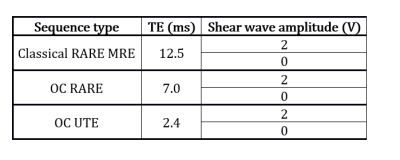
MRI measurements were run on a Bruker 4.7T small animal MRI system. For the OC techniques, the pulse was optimized for an excitation frequency of 400 Hz, a T2=26ms and a duration of 13.8ms. Three different sequences with unchanged TR and geometry were used: classical RARE MRE, OC RARE and OC UTE (Figure 2). Acquisitions with (400Hz shear wave) and without mechanical excitation were acquired. Two acquisitions with inversion of the polarity were always performed for phase images subtraction to remove static phase errors.

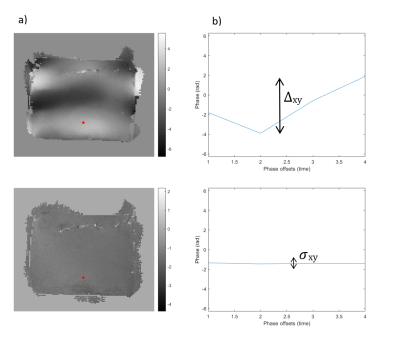
The phase to noise ratio PNR is calculated to evaluate and compare the motion encoding efficacy of the sequences. Since the SNR obtained from magnitude images cannot be directly used to compare radial and cartesian acquisitions, a phase method is used to calculate the noise level of the phase image. We defined the phase encoding $$$∆_{xy}$$$ as the maximal phase variation encoded in the (x,y) pixel along the temporal (phase offsets) direction. A ROI of 3600 pixels was defined to establish the limits of the phantom in the phase image. The PNR was computed as the ratio between the average value of phase encoding $$$ \bar{\Delta}$$$ obtained when a shear waves is propagating through the phantom and the phase noise $$$\sigma$$$, calculated as the mean phase encoding in the absence of mechanical excitation: $$PNR=\frac{\bar{\Delta}}{\sigma}=\frac{ \left(\displaystyle\sum_{(x,y)\in ROI} ∆_{xy} \right)_{MotionON}}{ \left(\displaystyle\sum_{(x,y)\in ROI} ∆_{xy} \right)_{MotionOFF}}$$.

Results

Phase images with and without excitation were analyzed. Shear wave phase images are shown in Figure 3 for each acquisition type. The wave propagation is perfectly visualized for all of them.
Figure 4 illustrates phase images of the OC UTE method and the respective temporal phase evolutions with and without excitation.
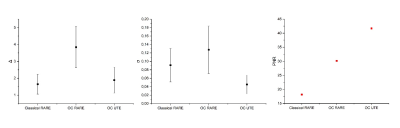
Figure 5 compares the results of the three presented MRE sequences in terms of $$$\bar{ \Delta}$$$, $$$\sigma$$$ and PNR. The OC RARE sequence produces the highest value of phase encoding but the OC UTE scheme achieves the lowest value of phase noise while yielding the best PNR. As a result, despite the difference between phantom’s T2-value and the T2 used for the pulse optimization, both OC methods present better PNR values compared to the classical RARE MRE. A gain of 2 in the PNR is reached when comparing the classical RARE MRE (TE=12.5ms) and the OC UTE (TE=2.4ms) methods.

Conclusion

A new motion encoding method consisting in appliying OC to MRE with a radial acquisition readout was demonstrated on phantom experiments. The OC pulse, which simultaneously performs frequency selective excitation and motion encoding, allows extremely short echo times yielding the highest PNR values when OC UTE is used. Future work will focus on evaluating the OC pulses robustness to the optimization parameters variation to improve the motion encoding of OC MRE methods. Pre-clinical studies on mice livers will be also conducted to evaluate the feasibility of the OC UTE method on in vivo experiments.

Acknowledgements

This work was performed within the scope of LABEX PRIMES (ANR-11-LABX-0063). Experiments were performed on the PILoT facility, part of the France Life Imaging infrastructure (ANR-11-INBS-0006).