0167
TURBINE-MRE: A 3D Hybrid Radial-Cartesian EPI Acquisition for MR Elastography1Radiology, Mayo Clinic, Rochester, MN, United States, 2Physiology and Biomedical Engineering, Mayo Clinic, Rochester, MN, United States
Synopsis
This study demonstrates the technical feasibility of a 3D radially batched internal navigator echo magnetic resonance elastography (TURBINE-MRE) technique in the brain. The highly efficient TURBINE-MRE approach allows for a true 3D wave displacement field to be acquired over the entire human brain volume in approximately 1.5 minutes.
Introduction
MR elastography (MRE) has been a useful tool for studying changes in the mechanical properties of brain tissues due to neurodegenerative diseases or normal aging.1 In more recent studies, there are increasing interests to investigate the dynamic changes of brain tissue properties related to cerebral arterial pulsation,2 and to detect fast neuronal activity using functional MR Elastography.3 A high spatial and temporal resolution MRE acquisition is desired for these applications, which is challenging for the 2D Cartesian acquisitions typically used in MRE. Recently, a 3D hybrid radial-EPI readout scheme (TURBINE) was proposed.4,5 The radially rotating EPI blades can provide motion robustness and higher temporal resolution when combined with a golden-angle scheme, a sliding window view-sharing technique,6 and advanced reconstruction.7 To date, the TURBINE technique has been successfully applied to DWI4 and fMRI5 that only display and process magnitude information. However, its ability to obtain stable and accurate phase images (essential for MRE) has not been demonstrated. In this preliminary work, we developed a TURBINE-MRE sequence and demonstrated its feasibility in a phantom and 6 volunteers as the first steps towards future advanced applications.Method
Pulse sequence: The proposed TURBINE-MRE sequence is based on a spoiled gradient-echo MRE sequence with a modified EPI readout (Fig.1a). MRE motion-encoding gradients (MEGs) were added before EPI readout to encode MRE harmonic tissue motion into the image phase. The EPI readout axis, Gθ, rotated about the phase-encoding axis in successive TRs by a golden angle increment.Phantom study: A gelatin brain phantom with stiff, spherical inclusions was scanned on a compact 3T scanner (GE Healthcare, Waukesha, WI)8,9 with a 32-channel head coil. The TURBINE-MRE data were acquired with a 2.5 mm isotropic resolution and 80 Hz vibration. For comparison, a standard 2D, multislice, spin-echo EPI-MRE acquisition was also performed.
In vivo study: To verify the in-vivo feasibility of the technique, six healthy volunteers were scanned with the same setup as the phantom study except a 60 Hz vibration was used to compensate for the wave damping in the brain. In addition, we also collected 2 mm isotropic data on three additional healthy volunteers to demonstrated its capability of acquiring high spatial resolution MRE images. The imaging parameters are summarized in the table in Figure 1.
Image Reconstruction: After EPI phase correction on every EPI blade, Tikhonov-Regularized SENSE10,11 reconstruction of the multi-coil 3D radial-Cartesian TURBINE data was then performed via a conjugate-gradient method using NUFFT regridding12, a Tikhonov regularization parameter λ=0.001 and 40 iterations. The coil sensitivity profiles were estimated from a separate calibration scan using a gradient echo sequence. To study the acceleration potential of TURBINE-MRE, a subset of the EPI blades (16, 32, 64 or 128 blades) was used for image reconstruction and MRE inversion and compared against the full 192-blade result.
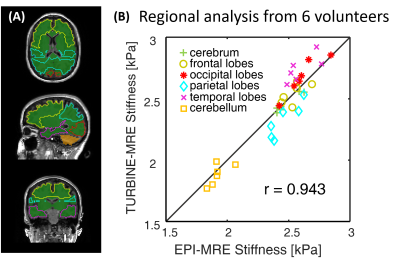
Regional brain stiffness analysis: MRE stiffness maps were generated using a 3D direct inversion (DI) algorithm to invert the wave-field as described elsewhere.13,14 The regional brain stiffness analysis was done in a similar approach as described in the previous study.14 Briefly, six regional ROIs (Fig.3) were generated from T1-weighted images, and then registered to the MRE magnitude images and propagated to the stiffness maps. The median stiffness values in each ROI were used for comparison. Pearson correlation was used to assess the agreement between EPI-MRE and TURBINE-MRE.
Results
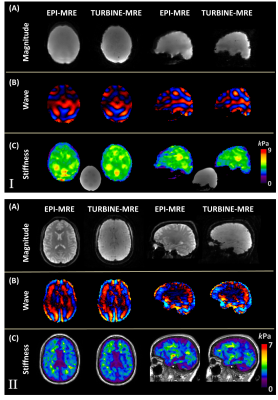
Figure 2 compares the phantom and the volunteer results between EPI-MRE and TURBINE-MRE. The TURBINE-MRE magnitude images have low contrast between tissues since the Ernst angle was chosen for the flip angle to maximize the signal intensity rather than the contrast. Comparable wave and stiffness maps were observed, but the 3D-TURBINE-MRE exhibited much less of the slice-to-slice variation artifacts that are commonly seen in the 2D-EPI-MRE acquisitions.Figure 3A illustrates the generated regional ROIs of a representative volunteer, and Figure 3B shows the scatter plot of the median regional stiffness measured from the six volunteers. A strong linear correlation (r=0.943) was observed between the two methods.
Figure 4 shows the relation between the stiffness values obtained from 16, 32, 64, or 128 blades against that of all 192 blades. Using the current basic reconstruction setup, the stiffness values were slightly underestimated at a small number of blades (e.g. N=16 or 32). However, with as few as 64 blades (a 1:20 minutes scan), the stiffness estimation was almost identical to that of 192 blades (r=0.999), demonstrating the high acceleration capability of the TURBINE-MRE sequence.
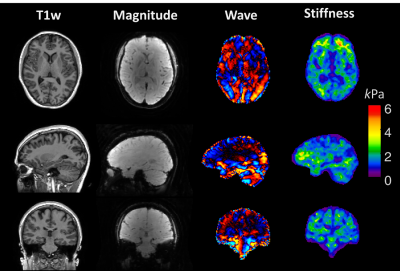
Figure 5. shows the 2 mm isotropic high-resolution TURBINE-MRE data. High-resolution wave and stiffness maps can be obtained within 6 minutes.
Discussion and Conclusion
Using the basic Tikhonov-SENSE reconstruction, a 1:20 minute TURBINE-MRE scan can be achieved. It is encouraging to explore more advanced reconstruction setups (e.g. a wavelet-sparse FISTA model) to further accelerate the sequence using fewer blades. The TURBINE-MRE sequence is also self-navigated, therefore it can be suitable for imaging fast dynamic stiffness changes and/or moving objects with further development. This phantom and in-vivo brain study demonstrated the feasibility of TURBINE-MRE for acquiring true 3D, high-resolution MRE data in a highly efficient manner, which motivates further exploration of its use for other applications such as functional MRE, free-breathing liver and cardiac MRE.Acknowledgements
This work was supported by grants from the National Institute of Health (R01 EB001981, R01 EB010065, R01 NS113760, NIBIB EB017197, and NIH U01 EB024450).References
1. Murphy MC, Huston J, 3rd, Ehman RL. MR elastography of the brain and its application in neurological diseases. Neuroimage 2017.
2. Schrank F, Warmuth C, Tzschatzsch H, Kreft B, Hirsch S, Braun J, Elgeti T, Sack I. Cardiac-gated steady-state multifrequency magnetic resonance elastography of the brain: Effect of cerebral arterial pulsation on brain viscoelasticity. J Cereb Blood Flow Metab 2019:271678X19850936.
3. Patz S, Fovargue D, Schregel K, Nazari N, Palotai M, Barbone PE, Fabry B, Hammers A, Holm S, Kozerke S, Nordsletten D, Sinkus R. Imaging localized neuronal activity at fast time scales through biomechanics. Sci Adv 2019;5(4).
4. McNab JA, Gallichan D, Miller KL. 3D steady-state diffusion-weighted imaging with trajectory using radially batched internal navigator echoes (TURBINE). Magn Reson Med 2010;63(1):235-242.
5. Graedel NN, McNab JA, Chiew M, Miller KL. Motion correction for functional MRI with three-dimensional hybrid radial-Cartesian EPI. Magn Reson Med 2016.
6. Jonathan SV, Vakil P, Jeong YI, Menon RG, Ansari SA, Carroll TJ. RAZER: A Pulse Sequence for Whole-Brain Bolus Tracking at High Frame Rates. Magnetic Resonance in Medicine 2014;71(6):2127-2138.
7. Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn Reson Med 2016;75(2):775-788.
8. Weavers PT, Shu YH, Tao SZ, Huston J, Lee SK, Graziani D, Mathieu JB, Trzasko JD, Foo TKF, Bernstein MA. Technical Note: Compact three-tesla magnetic resonance imager with high-performance gradients passes ACR image quality and acoustic noise tests. Medical Physics 2016;43(3):1259-1264.
9. Tan ET, Lee SK, Weavers PT, Graziani D, Piel JE, Shu Y, Huston J, 3rd, Bernstein MA, Foo TK. High slew-rate head-only gradient for improving distortion in echo planar imaging: Preliminary experience. J Magn Reson Imaging 2016;44(3):653-664.
10. King K, Angelos L. SENSE image quality improvement using matrix regularization. 2001. p 1771.
11. Pruessmann KP, Weiger M, Bornert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med 2001;46(4):638-651.
12. Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min-max interpolation. Ieee T Signal Proces 2003;51(2):560-574.
13 Manduca A, Oliphant TE, Dresner MA, Mahowald JL, Kruse SA, Amromin E, Felmlee JP, Greenleaf JF, Ehman RL. Magnetic resonance elastography: Non-invasive mapping of tissue elasticity. Medical Image Analysis 2001;5(4):237-254.
14. Murphy MC, Huston J, 3rd, Jack CR, Jr., Glaser KJ, Senjem ML, Chen J, Manduca A, Felmlee JP, Ehman RL. Measuring the characteristic topography of brain stiffness with magnetic resonance elastography. PLoS One 2013;8(12):e81668.
Figures