0151
Towards Real-Time Beam Adaptation on an MRI-Linac using AUTOMAP1ACRF Image X Institute, Faculty of Medicine and Health, The University of Sydney, Sydney, Australia, 2A. A. Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 3Department of Physics, Harvard University, Cambridge, MA, United States, 4Dipartimento di Elettronica, Informazione e Bioingegneria, Politecnico di Milano, Milan, Italy, 5Harvard Medical School, Boston, MA, United States
Synopsis
MRI-Linacs are new cancer treatment machines integrating radiotherapy with MRI. Dynamically adapting the radiation beam on the basis of MR-detected anatomical changes (e.g. respiratory and cardiac motion) promises to increase the accuracy of MRI-Linac treatments. A key challenge in real-time beam adaptation is accurately reconstructing images in real time. Historically, reconstruction of data acquired with accelerated techniques, such as compressed sensing, has been very slow. Here, we use AUTOMAP, a machine-learning framework, to quickly and accurately reconstruct radial MRI data simulated from a digital thorax phantom. These results will guide development of real-time adaptation technologies on MRI-Linacs.
Introduction
MRI-Linacs are cutting-edge treatment machines that combine the unrivalled image quality of MRI with a linear accelerator (linac) for x-ray radiation therapy.[1] Commercial MRI-Linacs are already enabling new standards of precision radiotherapy.[2] However, the implementation of multi-leaf collimator (MLC) tracking (see Fig.1), which can dynamically adapt the radiation beam to tumour motion, promises to further improve the accuracy of MRI-Linac treatments, improving patient outcomes and reducing side effects.[3]Fast acquisitions based on Golden-angle radial trajectories have shown much promise for motion tracking during MRI-Linac treatments as they enable reconstruction of high-spatial-resolution, motion-averaged images in parallel with high-temporal-resolution images using the same raw data.[4] However, compressed sensing reconstruction of undersampled radial data is computationally expensive, presenting a barrier to the real-time imaging required for dynamic treatment adaptation.[5]
Recently, automated transform by manifold approximation (AUTOMAP) has been developed as a generalized reconstruction framework that learns the relationship between the raw MR signal and the target image domain.[6] Once trained, this machine-learning-based framework reconstructs images in a single forward pass.
Here, we train AUTOMAP to reconstruct MR data acquired with a heavily undersampled Golden-angle radial trajectory. Using data simulated from a digital MRI phantom,[7] we compare the performance of AUTOMAP to conventional iterative methods for compressed sensing reconstruction, showing AUTOMAP gives similar reconstruction accuracy but with much faster processing times.
Methods
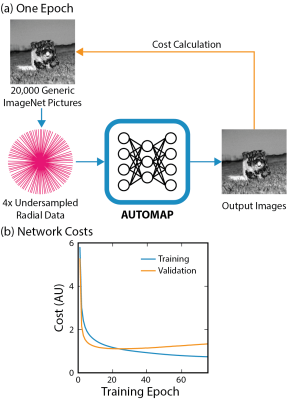
Data Preprocessing: Datasets of 20,000 training images and 1,000 validation images depicting generic objects were sourced from ImageNet.[8] Using MATLAB, ImageNet data was preprocessed to normalized, grayscale images at 128 × 128 resolution.A Golden-angle radial trajectory with 4× undersampling in the partition direction and 25% oversampling in the readout direction was defined using the BART toolbox.[9] A nonuniform fast Fourier Transform (NUFFT) was used to encode this trajectory, generating k-space data for a single coil. Additive white Gaussian noise (AWGN, 25 dB) was applied to k-space, simulating real-world sensor noise.
Neural Network Architecture and Hyperparameters: We implemented AUTOMAP in TensorFlow using the architecture described in reference [6]. This model inputs raw k-space data and outputs an image. In summary, the TensorFlow-based network consists of 2 fully connected layers, 2 convolutional layers and 1 deconvolutional layer. Training over 75 epochs on a local server with one 12-GB GPU took approximately 4 hours.
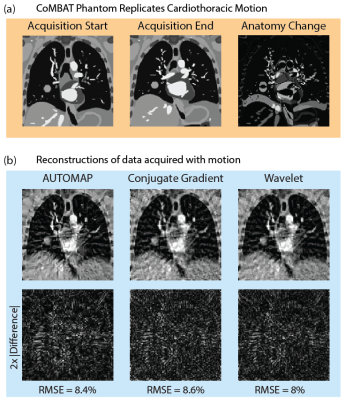
Image Reconstruction: Four-dimensional thoracic MRI volumes were generated using the digital CT/MRI breathing XCAT (CoMBAT) phantom.[7] Two-dimensional slices, containing a spherical lung tumour undergoing realistic cardiothoracic motion, were extracted from these volumes at 128 × 128 resolution.[10,11] MRI signal intensity was simulated for a spoiled gradient echo sequence. Simulated 2D slices were encoded to a radial trajectory using NUFFT processing.
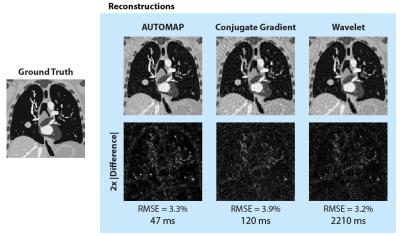
The trained AUTOMAP model was used to reconstruct 2D CoMBAT images from radial data via one forward pass. For comparison, wavelet and conjugate gradient (CG) techniques for reconstructing undersampled data were implemented in MATLAB from code in reference [12]. Root mean square errors (RMSE) were normalized by the root mean square magnitude of the ground truth image.
Results
AUTOMAP was successfully trained on 4× undersampled radial data (Fig 2a). A minimum in the validation cost curve occurred at the 20th training epoch (see Fig. 2b) and early stopping was used to save these weights for reconstruction.CoMBAT generated a static ground truth anatomy (simulation TR/TE = 4.8/2.0 ms) which was encoded via a radial trajectory with AWGN. Reconstruction results (Fig. 3) show that AUTOMAP reconstructs with an accuracy (RMSE 3.3%) close to that of wavelet reconstruction (RMSE 3.2%) whilst being nearly 50 times faster to execute. Both techniques outperformed conjugate gradient reconstruction (RMSE 3.9%). The 47 ms AUTOMAP reconstruction time shows no significant increase when up to 20 trajectories are computed in parallel due to the nature of GPU processing.
To test reconstruction of motion-averaged images, CoMBAT was used to generate a time-series of 51 ground truth images in 20 ms steps as shown in Fig 4a (simulation TR/TE = 20/8 ms). K-space was simulated by extracting sequential spokes from corresponding ground truth images. AUTOMAP, conjugate gradient and wavelet techniques all show similar degradation in image quality with significant blurring of the moving tumour (RMSE error was evaluated relative to the last ground truth image in the time-series).
Discussion
Our results leverage recent advances in machine learning to implement fast reconstructions of undersampled radial data on a dynamic tumour model with accuracy similar to slower iterative reconstruction techniques. Integrating AUTOMAP with fast data streaming tools [13], MLC tracking algorithms [14] and 3D radial acquisitions [15] will be crucial for use with MRI-Linac beam adaptation technologies.Future improvements will exploit temporal correlations in the sampling of training data to deblur reconstructed images with AUTOMAP.[4] Training on domain-specific datasets that reflect target anatomy will improve reconstruction accuracy.[6] Comprehensively evaluating the speed of AUTOMAP relative to other machine-learning-based [16] and GPU-optimized reconstruction techniques will also be crucial.[17]
Conclusion
We have used AUTOMAP to accurately and rapidly reconstruct radially-acquired images of a digital cardiothoracic MRI phantom. These results will inform the future development of dynamic adaptation technologies for MRI-Linacs, enabling new standards of personalized radiotherapy.Acknowledgements
This work has been funded by the Australian National Health and Medical Research Council Program Grant APP1132471. The authors are grateful to Julia Johnson for graphical design assistance.References
[1] G.P. Liney, B. Whelan, B. Oborn, M. Barton, P. Keall, Clin Oncol 30 (2018) 686–691.
[2] J.R. van Sörnsen de Koste, M.A. Palacios, A.M.E. Bruynzeel, B.J. Slotman, S. Senan, F.J. Lagerwaard, Int J Radiat Oncol Biol Phys 102 (2018) 858–866.
[3] E. Colvill, J.T. Booth, R.T. O’Brien, T.N. Eade, A.B. Kneebone, P.R. Poulsen, P.J. Keall, Int J Radiat Oncol Biol Phys 92 (2015) 1141–1147.
[4] T. Bruijnen, B. Stemkens, J.J.W. Lagendijk, C.A.T. Van Den Berg, R.H.N. Tijssen, Phys Med Biol 64 (2019).
[5] L. Feng, L. Axel, H. Chandarana, K.T. Block, D.K. Sodickson, R. Otazo, Magn Reson Med 75 (2016) 775–88.
[6] B. Zhu, J.Z. Liu, B.R. Rosen, M.S. Rosen, Nature 555 (2018) 487–492.
[7] C. Paganelli, P. Summers, C. Gianoli, M. Bellomi, G. Baroni, M. Riboldi, Med Biol Eng Comput 55 (2017) 2001–2014.
[8] J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, L. Fei-Fei, IEEE Conf ‘Computer Vis Pattern Recognit (2009) 248–255.
[9] M. Uecker, F. Ong, J.I. Tamir, D. Bahri, P. Virtue, J.Y. Cheng, T. Zhang, M. Lustig, in: Proc 23rd Annu Meet ISMRM, 2015, p. 2486.
[10] W.P. Segars, G. Sturgeon, S. Mendonca, J. Grimes, B.M.W. Tsui, Med Phys 37 (2010) 4902–4915.
[11] T. Reynolds, C.C. Shieh, P.J. Keall, R.T. O’Brien, Med Phys 49 (2019) 4116–4126.
[12] M. Guerquin-Kern, M. Haberlin, K.P. Pruessmann, M. Unser, IEEE Trans Med Imaging 30 (2011) 1649–1660.
[13] P.T.S. Borman, B.W. Raaymakers, M. Glitzner, Phys Med Biol 64 (2019) 185008.
[14] J. Toftegaard, P.J. Keall, R. O’Brien, D. Ruan, F. Ernst, N. Homma, K. Ichiji, P.R. Poulsen, Med Phys 45 (2018) 2218–2229.
[15] G. Bauman, O. Bieri, Magn Reson Med 76 (2016) 583–590.
[16] F. Liu, A. Samsonov, L. Chen, R. Kijowski, L. Feng, Magn Reson Med (2019) 1890–1904.
[17] H. Wang, H. Peng, Y. Chang, D. Liang, Quant Imaging Med Surg 8 (2018) 196–208.
Figures