0134
Diffusion tensor distribution imaging of brain tumor microstructure and heterogeneity1Random Walk Imaging, Lund, Sweden, 2United Imaging Healthcare, Shanghai, China, 3Zhongnan Hospital of Wuhan University, Wuhan, China, 4Lund University, Lund, Sweden
Synopsis
For voxels containing multiple cell or tissue types, DTI metrics are challenging to interpret in terms of specific microstructural properties. We address this problem by adapting encoding and inversion strategies from solid-state and low-field NMR to determine diffusion tensor distributions (DTDs) with dimensions corresponding to cell densities, shapes, and orientations. Three patients with glioma, meningioma, or cerebral cyst underwent 5 min DTD imaging giving 15 distinct parameter maps for quantitative analysis and intuitive microsctructural interpretation. The DTD-derived metrics showed good agreement with expected tissue properties and structural insights not accessible with DTI.
Introduction
Water diffusion in tissue is influenced by the microstructural organization and permeability of the cell membranes (see Fig.1A). Conventional diffusion tensor imaging (DTI)1 gives voxel-averaged metrics such as mean diffusivity (MD) and fractional anisotropy (FA) that have been used to probe the densities2 and shapes3 of cells in brain tumors, but give ambiguous results whenever the analysed voxel comprises multiple tissue environments with different properties.4,5 Higher specificity is achieved with diffusion tensor distribution (DTD) imaging6 building on encoding7 and inversion8 strategies from solid-state and low-field NMR to quantify sub-voxel heterogeneity as 4D DTDs with isotropic diffusivity Diso (“size”), normalized anisotropy DΔ (“shape”), and orientation (θ,φ) dimensions, thus achieving a more detailed description of sub-voxel tissue structure. While conventional DTI can be acquired with off-the-shelf pulse sequences, the additional information and specificity of our approach rely on custom sequences and high-performance scanner hardware. We apply DTD imaging in patients with glioma, meningioma, or cerebral cyst, showing that DTD-derived parameter maps allow for intuitive microstructural interpretations consistent with expected tissue properties.Methods
Patient selection: We scanned three patients with different biopsy-proven pathologies: meningioma (WHO grade I), glioma (WHO grade IV), and cerebral cyst. All patients were scanned prior to surgical treatment. The study was approved by the IRB of the Zhongnan Hospital of Wuhan University, Wuhan, China.Acquisition protocol: Measurements were performed on a UIH uMR 790 3.0 T system (United Imaging Healthcare, Shanghai, China) with 100 mT/m gradients on axis and a 24-channel head coil. Images were acquired with a custom spin echo-prepared free gradient waveform EPI sequence9 using TE=84.9 ms, TR=3438 ms, whole brain coverage, FOV = 224×224 mm, matrix = 112×112, bandwidth = 1560 Hz/pixel, partial Fourier factor = 0.75, in-plane parallel imaging factor = 2 (anterior-posterior). The meningioma data was collected using a spatial resolution of 2×2×4 mm3, and 25 slices separated by 1 mm gaps; while the glioma and cyst datasets had a voxel-size of 2×2×5 mm3, and comprised 23 slices separated by 1 mm gaps. Diffusion encoding was performed with numerically optimized10,11 gradient waveforms for 80 b-tensors spread out over b-values (100, 700, 1400, and 2000 smm–2), normalized shapes bΔ = 0 and 1,12 and 40 directions. The total scan time was under 5 min.
Diffusion tensor distributions: The acquired data was converted to voxel-wise DTDs using a stochastic iterative algorithm13 approximating the underlying DTD as a discrete set of 20 different {Diso,n,DΔ,n,θn,φn}1≤n≤20 coordinates and their respective {wn}1≤n≤20 weights. Bootstraping with replacement14 was used to estimate ensembles of 96 plausible solutions and derive uncertainty metrics.
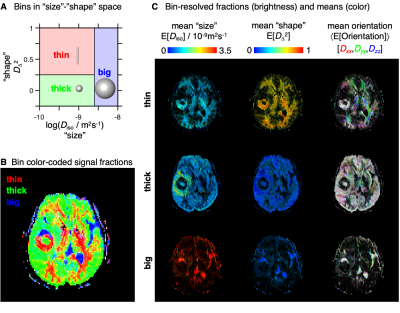
Parameter maps: The spatially-resolved DTDs were converted to a set of parameter maps informing about the "sizes", "shapes", and orientations of the diffusion tensors originating from various sub-voxel tissues.6 Dividing the DTD into smaller subspaces (‘bins’) allowed separation of signal contributions from different tissues and the calculation of per-bin means of size, shape, and orientation metrics.
Results & Discussion
Fig. 1B shows that white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) are all characterized by distinctive distributions that capture their corresponding diffusion properties; WM: low Diso, high DΔ2 (densely packed elongated cells); GM: low Diso, low DΔ2 (densely packed isotropic cells); CSF: high Diso, low DΔ2 (no cells). Diseased tissues were found to possess distinct diffusion properties. For the example in Fig. 1B, we observe that edema is characterized by intermediate Diso and low DΔ2, (loosely packed or permeable cells), while glioma tissue exhibits both low Diso and low DΔ2 (densely packed isotropic cells). The absence of anisotropic components in the glioma hints at a destruction of the underlying WM.Fig. 2 displays maps derived from the entire DTD space. The S0 map provides T2-weighted contrast, while the E[Diso] is equivalent to the common MD metric. The meningioma and the cyst exhibit high E[DΔ2] and no dominant color in the E[Orientation] map, corresponding to elongated cells with low orientational order. Convolution of the E[DΔ2] and E[Orientation] parameters yields the conventional FA metric where the fundamentally different pieces of information about cell shapes and orientations are inextricably entangled. The heterogeneity metric Var[Diso] is elevated in voxels containing both tissue and CSF.
The binning process is schematized in Fig. 3A, and maps with per-bin fractions and means are shown in Figs. 3B-C and 4. The global and bin-resolved maps reveal that the meningioma presents low Diso, high DΔ2, and no dominant color in directionally color-coded DΔ2, corresponding to densely packed elongated cells without orientational order. Conversely, the glioma exhibits low Diso and low DΔ2, indicating densely packed isotropic cells. The intracranial cyst features a core resembling the glioma and a shell with orientationally disordered elongated cells reminiscent of the meningioma.
Conclusions
The proposed framework with spatially-resolved DTDs is capable of resolving and characterizing sub-voxel tissue environments that are indistinguishable in conventional DTI. The parameter maps with statistical descriptors and bin-resolved means derived from the DTDs displayed good contrast between different tissues types and provide valuable insight into the microstructural properties of the three studied pathologies. Moreover, this protocol does not require prior knowledge of the underlying structure, meaning that it shows good promise in exploratory clinical studies such as characterization of anomalous brain tumors.Acknowledgements
Data collection was approved by the Zhongnan Hospital of Wuhan University ethics committee and with written informed consent from all participants. This work was financially supported by the Swedish Foundation for Strategic Research (AM13-0090, ITM17-0267) and the Swedish Research Council (2018-03697). Daniel Topgaard owns shares in Random Walk Imaging (RWI) AB (Lund, Sweden, http://www.rwi.se/), holding patents related to the described methods. Markus Nilsson and Filip Szczepankiewicz are gratefully acknowledged for generously sharing know-how on pulse sequence setup acquired during their RWI-funded research and employment.References
1. Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B 1996;111:209-219.
2. Padhani AR, Liu G, Mu-Koh D, Chenevert TL, Thoeny HC, Takahara T, Dzik-Jurasz A, Ross BD, Van Cauteren M, Collins D, Hammoud DA, Rustin GJS, Taouli B, Choyke PL. Diffusion-weighted magnetic resonance imaging as a cancer biomarker: Consensus and recommendations. Neoplasia 2009;11:102-125.
3. Peet AC, Arvanitis TN, Leach MO, Waldman AD. Functional imaging in adult and paediatric brain tumours. Nat Rev Clin Oncol 2012;9:700-711.
4. Jones DK, Cercignani M. Twenty-five pitfalls in the analysis of diffusion MRI data. NMR Biomed 2010;23:803-820.
5. Zatorre RJ, Fields RD, Johansen-Berg H. Plasticity in gray and white: neuroimaging changes in brain structure during learning. Nat Neurosci 2012;15:528-536.
6. Topgaard D. Diffusion tensor distribution imaging. NMR Biomed 2019;32:e4066.
7. Frydman L, Chingas GC, Lee YK, Grandinetti PJ, Eastman MA, Barrall GA, Pines A. Variable-angle correlation spectroscopy in solid-state nuclear magnetic resonance. J Chem Phys 1992;97:4800-4808.
8. Prange M, Song YQ. Quantifying uncertainty in NMR T2 spectra using Monte Carlo inversion. J Magn Reson 2009;196:54-60.
9. Topgaard D. Multidimensional diffusion MRI. J Magn Reson 2017;275:98-113.
10. Sjölund J, Szczepankiewicz F, Nilsson M, Topgaard D, Westin C-F, Knutsson H. Constrained optimization of gradient waveforms for generalized diffusion encoding. J Magn Reson 2015;261:157-168.
11. Szczepankiewicz F, Westin CF, Nilsson M. Maxwell-compensated design of asymmetric gradient waveforms for tensor-valued diffusion encoding. Magn Reson Med 2019;82:1424-1437.
12. Eriksson S, Lasič S, Nilsson M, Westin C-F, Topgaard D. NMR diffusion encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. J Chem Phys 2015;142:104201.
13. de Almeida Martins JP, Topgaard D. Multidimensional correlation of nuclear relaxation rates and diffusion tensors for model-free investigations of heterogeneous anisotropic porous materials. Sci Rep 2018;8:2488.
14. de Kort DW, van Duynhoven JP, Hoeben FJ, Janssen HM, Van As H. NMR nanoparticle diffusometry in hydrogels: enhancing sensitivity and selectivity. Anal Chem 2014;86:9229-9235.
Figures
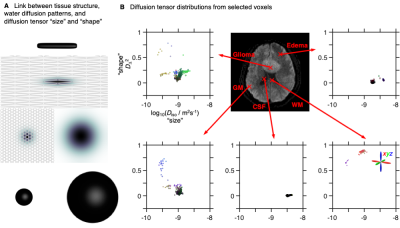
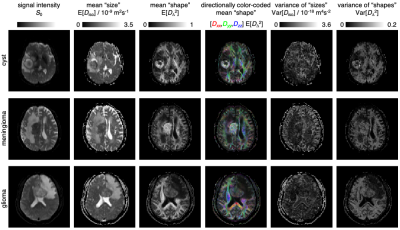
Fig. 2: DTD parameter maps for three patients with cerebral cyst, meningioma, or glioma. The maps show statistical descriptors derived from the per-voxel DTDs: signal S0, mean "size" E[Diso], mean "shape" E[DΔ2], directionally color-coded mean "shape", variance of "sizes" Var[Diso], and variance of "shapes" Var[DΔ2].