0123
Required number of tissue compartments for electromagnetic safety simulation of the head: personalized RF safety for 7T pTx1Wellcome Centre for Integrative Neuroimaging, FMRIB Division, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, 2Oxford Centre for Clinical Magnetic Resonance Research, Department of Cardiovascular Medicine, University of Oxford, Oxford, United Kingdom
Synopsis
Personalized electromagnetic simulation models can be generated by segmenting MR-images. However, it is unclear how many tissue types are required for accurate 7T head models. Here, a clustering approach is used to determine the error in the simulated pTx SAR for models with different numbers of tissue types (clusters). Models consisting of only four different tissue types plus air were found to consistently generate low errors for human body-models of different ages and genders. Using the proposed method, it should be possible to operate scanners closer to the true SAR limits due to improved estimations of the actual patient-specific SAR.
Introduction
The Specific Absorption Rate (SAR) is a limiting factor in many MRI scans. Computational simulations based on high-resolution human body models can be used to estimate SAR, but such models are not available for individual patients in a clinical setting. To account for inter-patient variability, which makes it difficult to accurately determine the pTx SAR distribution for individual patients, an additional uncertainty margin of up to 50%1 is required. Previous work has generated personalized SAR models from fat, lung, and water images for 3T whole-body MRI2, and based on fat, muscle, and skin-images for prostate at 7T3, but it remains unclear how this translates to 7T-pTx4 in the head. Warping of well-characterised models to match the anatomy of individual patients has been studied for 7T-pTx head coils5, but was found to result in limited improvement in accuracy of the simulations. Here, we determine a minimum number of tissue compartments required to accurately predict SAR for 7T-pTx. These results are useful for identifying a minimum set of tissue contrasts required to generate personalized SAR models by segmenting MR images.Methods
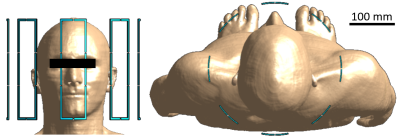
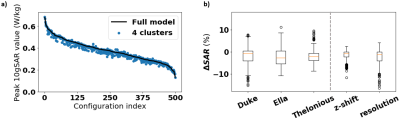
High-resolution human body models from the Virtual Population v3.0 (ViP) provided by the IT’IS Foundation (Zurich, Switzerland)6 were used for simulations. The approximately 40 different tissue types within the simulated head regions of the ViP Duke (male, 34 y, 1.77 m), Ella (female, 26 y, 1.63 m), and Thelonious (male, 6 y, 1.15 m) models were grouped into simplified clusters of tissues using a k-means7 clustering approach in a conductivity-permittivity-density hyperspace, in which models consisting of between 1 and 6 clusters were generated. The tissues in each cluster were assigned optimized values for the dielectric properties based on the results of the k-means clustering. Electromagnetic SAR simulations were carried out using the software package Sim4Life by Zurich MedTech (ZMT, Zurich, Switzerland) at the 7T hydrogen frequency of 298 MHz. An optimized 8-channel pTx-coil with a normalized total input power of 1 W was used to carry out the simulations. The simulation setup with Duke in the coil is shown in Figure 1. For each clustered model, a comparison was made between the simulation results of the full 40-tissue model and those of the respective simplified n-cluster model. After running simulations in Sim4Life, a Q-matrix8 was calculated9 for every voxel in the model to determine the voxel’s overall maximum SAR for all possible B1-shims10,11. In addition, the Q-matrices were used to assess the peak-SAR and the SAR distribution for 500 random, normalized B1 shims. 10-gram averaging volumes, determined in accordance with the IEEE/IEC 62704-1 standard12, were used for calculating all SAR values. Once the optimal set of clusters was established for Duke, the model was applied to both Ella and Thelonious, and the resulting SARs were compared to the simulation results for the respective full models.Results
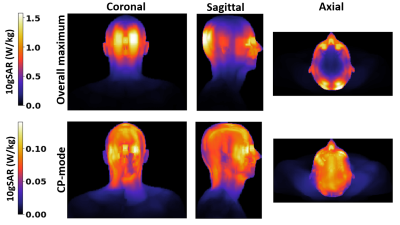
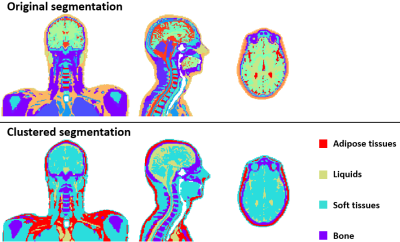
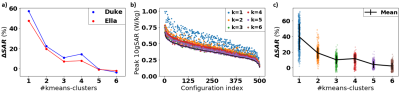
The ‘ground truth’ SAR distributions for the original 40-tissue Duke model are shown in Figure 2. The clustered segmentation of these tissues in Duke for both the original model and a 5-cluster case can be seen in Figure 3. Figure 4 shows that when clustering the tissues of Duke and Ella, both the overall peak-SAR and the peak SAR for the 500 random B1 shims converge to close to the full model-values (errors of 4.1±4.3%) for ≥5 clusters. Analysis of those 5 k-means clusters showed that they roughly consist of adipose tissues, liquids, soft tissues, bone, and air, with numerically optimized dielectric properties that closely approximate the dielectric properties of fat, CSF, grey matter, cortical bone, and air in the original model13. The simulation results when segmenting Duke using the original values of those tissues also reproduce the SARs with high accuracy (Figure 5). For all models, the peak SAR for the 500 random B1 shims can be determined with an absolute error of less than 12% for over 99% of the shims. Figure 5b shows that this result is found to also be consistent for Ella and Thelonious, and when running simulations using different simulation settings. The overall peak SAR for all voxels in the simplified cluster model is 3.5% lower than in the original model for Duke, 3.4% lower for Ella, and 2.2% lower for Thelonious.Discussion
The k-means-based segmentations indicate that no more than five different tissue types (including air) are required to accurately estimate SAR in the head region at 7T. When using clusters consisting of adipose tissues, liquids, soft tissues, and bone for this, the resulting errors are significantly smaller than the 50%-error margin which has previously been reported for determining individual-subject SAR based on electromagnetic simulations from a generic model. The errors in the extreme case of the overall highest SAR value for any possible B1 shim are even smaller. These results seem consistent for models of different genders and ages, and when using different simulation settings. For the proposed segmentation, we envisage that an automated segmentation based on preliminary MR-images for individual patients should be possible.Conclusions
It was found that a minimum number of five tissue compartments (including air) is required to generate personalized SAR models. These results should enable MR scanners to operate closer to the true SAR-limits.Acknowledgements
No acknowledgement found.References
[1] M. Le Garrec, V. Gras, M.-F. Hang, G. Ferrand, M. Luong, and N. Boulant, Probabilistic analysis of the specific absorption rate intersubject variability safety factor in parallel transmission MRI, Magnetic Resonance in Medicine 78, 1217 (2017).
[2] H. Homann, P. Börnert, H. Eggers, K. Nehrke, O. Dössel, and I. Graesslin, Toward individualized SAR models and in vivo validation, Magnetic Resonance in Medicine 66, 1767 (2011).
[3] Ö. Ipek, A.J. Raaijmakers, J.J. Lagendijk, P.R. Luijten, and C.A. van Den Berg, Intersubject local SAR variation for 7T prostate MR imaging with an eight‐channel single‐side adapted dipole antenna array, Magnetic Resonance in Medicine 71, 1559 (2014).
[4] F. Padormo, A. Beqiri, J. V. Hajnal, and S. J. Malik, Parallel transmission for ultrahigh-field imaging, NMR in Biomedicine 29, 1145 (2016).
[5] H. Jeong, J. Andersson, A.T. Hess, and P. Jezzard, Feasibility of personalized RF safety monitoring in pTx MRI using linear registration versus non-linear registration, ISMRM 27th Annual Meeting, (2019).
[6] M.C. Gosselin, E. Neufeld, H. Moser, E. Huber, S. Farcito, L. Gerber, M. Jedensjö, I. Hilber, F. Di Gennaro, B. Lloyd, and E. Cherubini, Development of a new generation of high-resolution anatomical models for medical device evaluation: the Virtual Population 3.0, Physics in Medicine & Biology 59, 5287 (2014).
[7] J. MacQueen, Some methods for classification and analysis of multivariate observations, Proceedings of the fifth Berkeley symposium on mathematical statistics and probability 1, 281 (1967).
[8] I. Graesslin, H. Homann, S. Biederer, P. Börnert, K. Nehrke, P. Vernickel, G. Mens, P. Harvey, and U. Katscher, A specific absorption rate prediction concept for parallel transmission MR, Magnetic Resonance in Medicine 68, 1664 (2012).
[9] A. Beqiri, J. W. Hand, J. V. Hajnal, and S. J. Malik, Local Q-matrix computation for parallel transmit MRI using optimal channel combinations, ISMRM 24th Annual Meeting, (2016).
[10] M. de Greef, O. Ipek, A. J. Raaijmakers, J. Crezee, and C. A. van den Berg, Specific absorption rate intersubject variability in 7T parallel transmit MRI of the head, Magnetic Resonance in Medicine 69, 1476 (2013).
[11] A. Sbrizzi, H. Hoogduin, J. J. Lagendijk, P. Luijten, G. L. Sleijpen, and C. A. Van Den Berg, Fast design of local N-gram-specific absorption rate-optimized radiofrequency pulses for parallel transmit systems, Magnetic Resonance in Medicine 67, 824 (2012).
[12] Standard for Determining the peak spatial-average specific absorption rate (SAR) in the human body from wireless communications devices, 30 MHz to 6 GHz - Part 1: General requirements for using the finite difference time domain (FDTD) method for SAR calculations, IEC/IEEE Standard 62704-1 (2017).
[13] P. Hasgall, F. Di Gennaro, C. Baumgartner, E. Neufeld, B. Lloyd, M. Gosselin, D. Payne, A. Klingenbock, and N. Kuster, “IT’IS Database for thermal and electromagnetic parameters of biological tissues”, version 4.0, (2018).
Figures