Introduction

The blood–brain barrier (BBB) plays a critical role in oxygen and nutrition delivery, clearance of toxic metabolites, and protection of the central nervous system (CNS) from infection¹. BBB breakdown is known to play a role early in the course of Alzheimer’s Disease(AD) based on CSF biomarker and imaging data in animal models and in patients. Recently, an Arterial Spin Labeling(ASL) based sequence is introduced to map the signal change in capillary and tissue compartment and derive water exchange rate (k_w)². However, composite RF pulses were used for the diffusion preparation leading to potential artifact near the edge of brain³. Also, The k_w fit to the fraction of capillary/tissue signal is very noise sensitive, which is exacerbated further by the low SNR in ASL. We propose to overcome these problems by using an adiabatic RF pulse³ and fit k_w directly to the signal equation of the two compartment signal equations.

Methods

Algorithm:
Recently, a capillary-tissue compartment model of pseudo-continuous ASL (pCASL) signal incorporating the exchange rate of water from blood to tissue was introduced⁴:
$$\Delta M_{b}(t)=-\frac{2CBF\varepsilon M_{0}\beta }{\lambda}[\frac{e^{-(R_{1a}-R_{1b}\tau_{\alpha})}}{R_{1b}}(e^{-R_1b(t-\delta )}-e^{-R_{1b}t})-e^{-(R_{1a}-\alpha)\tau_{a}}(e^{-\alpha(t-\delta)}-e^{-\alpha t})]\qquad (1)$$
$$\Delta M_{c}(t)=-\frac{2CBF\varepsilon M_{0}e^{-(R_{1a}-R_{1b})\tau_{a}} }{\lambda\alpha}(e^{-\alpha(t-\delta)}-e^{-\alpha t}) \qquad (2)$$
Where $$$\Delta M_{b}(t)$$$ and $$$\Delta M_{c}(t)$$$ are the signal in tissue and capillary compartments, respectively. CBF is cerebral blood flow, which is calculated from ASL data without diffusion preparation pulse⁵. $$$\varepsilon=0.8$$$ is tagging efficiency⁶. $$$M_0$$$ is proton density map. $$$\lambda = 0.9mL/g$$$ is the partition coefficient of water in the brain, $$$R_{1a} $$$ and $$$R_{1b} $$$ are longitudinal relaxation rate of blood and tissue, respectively⁶. We use $$$R_{1a}=0.6/s $$$ and $$$R_{1b} $$$ is acquired using FAST T1 mapping sequence. $$$\tau_a$$$ is arterial transit time and is set to 1.25s for healthy subjects². $$$\delta = 1.5s$$$ is labeling time. PLD=1.8s is post labeling delay and $$$t=\delta + PLD$$$. $$$\alpha = k_w + R_{1a}$$$ and $$$\beta = \frac{k_w}{k_w+R_{1a}-R_{1b}}$$$ are model paramters. $$$\Delta M_{b}(t)$$$ and $$$\Delta M_{c}(t)$$$ are acquired with/without diffusion preparation pulses²: $$\Delta M_{b}(t)+\Delta M_{c}(t)=b_0 \qquad (3) $$ $$\Delta M_{b}(t)=b_{50} \qquad (4) $$
Where $$$b_0$$$ and $$$b_{50}$$$ are the ASL image acquired with a diffusion preparation pulse that b-value= 0 and 50, respectively. Combining the equations above, $$$b_0$$$ and $$$b_50$$$ can be expressed as function of k_w: $$$b_0=f(k_w)$$$ and $$$b_{50}=g(k_w)$$$. We propose to solve k_w by minimizing the following equations using the Levenberg–Marquardt algorithm: $$k_w=argmin_{k_w}[||b_{50}-g(k_w)||^2_2+||b_{0}-f(k_w)||^2_2+\lambda||\nabla k_w||^2_2] \qquad (5) $$ where λ = 0.05 is the weighting factor balancing data fidelity and L2 penalty function.


Data acquisition and processing:
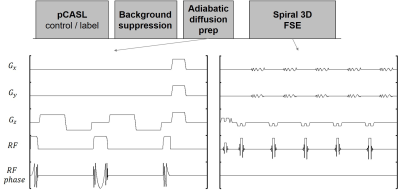
The existing acquisition approach for BBB permeability mapping is based on 3D Cartesian gradient and spin echo (GRASE) pulse sequence design and suffers from low spatial resolution (3.5x3.5x8 mm³) and limited brain coverage¹. To translate water exchange rate mapping into routine clinical imaging practice, we have developed an SNR efficient 3D stacks-of-spiral fast spin echo (FSE) pulse sequence for whole brain coverage with robust BIR-4 adiabatic diffusion preparation that can achieve 1.8x1.8x4 mm³ resolution (8-fold improvement compared to GRASE approach) in 4 min, which is shown in figure 1.
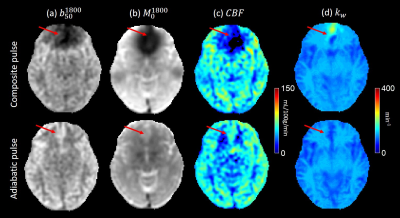
A symmetric nonselective bipolar gradient is applied along z axis to minimize eddy currents. Adiabatic RF pulses³ replace composite pulses to minimize artifacts at brain edge. A comparison of ASL data using these two RF pulses is shown in figure 2. A 3D fast spin echo readout is used to minimize acquisition time. 6 healthy subjects were scanned on a 3T GE scanner. Image parameters were: voxel size 1.875*1.875*4 mm³, field of view 24cm, number of slices 36. Duration of the four diffusion gradient lobes were 8.32ms and the amplitude was 3 gauss/cm resulting in b-value of 50. The k_w map was generated using Eq.5 and its value in different anatomical regions is calculated using an AAL atlas⁷.

Results

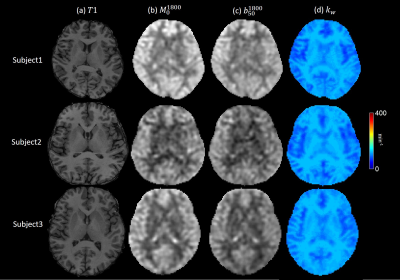
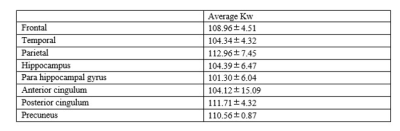
The use of composite pulse led to a severe signal loss near the brain periphery in both b₅₀ and M₀ images, resulting in a low estimate of CBF and a high estimate of k_w. k_w maps of 3 healthy subjects are shown in Figure 3. In all six subjects, white matter showed significantly higher k_w compared to gray matter, which is consistent with previous studies⁴. No obvious artifact was observed in the 6 subjects, suggesting the robustness of the sequence. Average k_w measurements of all subjects in 8 ROIs related to Alzheimer’s disease are shown in table 1.

Discussion and Conclusion

The image quality of water exchange rate mapping based on ASL was substantially improved by the use of adiabatic RF pulses, 3D fast spin echo readout and a direct fit of k_w to blood/tissue compartment signal equations. The measured k_w values in healthy subjects were similar to those measured in previous work². However, image resolution and quality was significantly improved while keeping scanning time the same. However, in our current method arterial transit time (ATT) was assumed to be constant. This assumption may not hold on AD patients. In previous work², ATT was calculated independently requiring 2 more sequences. Thus, further work will include solving ATT and k_w at the same time with minimum scan time increase.