Magnetic Field Shimming
1MRRC, Yale University, New Haven, CT, United States
Synopsis
Magnetic field inhomogeneity affects the performance of almost all MRI and MRS methods, leading to signal loss and image distortion in MRI and loss of spectral resolution in MRS. Spherical harmonics (SH) shimming is the standard tool to improve magnetic field homogeneity, but falls short on complex samples like the human head. The principles and practical aspects of SH shimming are discussed, together with more recent non-SH-based alternatives.
Introduction
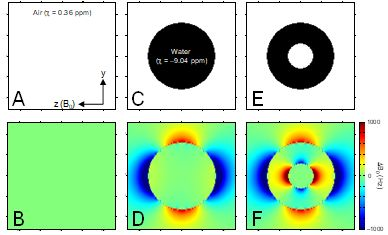
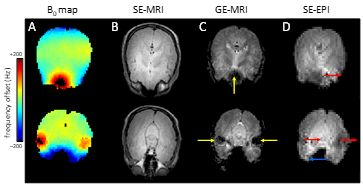
NMR is based on the fundamental property of nuclear spin which has both direction and amplitude. When placed in an external magnetic field nuclear spins have a slight preference to align themselves with the magnetic field thereby creating net, macroscopic magnetization. The magnetization can be rotated by a secondary, oscillating magnetic field in order to be detected as a damped, oscillating current in a receiving coil. From this viewpoint NMR can be seen as the manipulation of magnetization by a variety of static and dynamic magnetic fields. However, after the signal is acquired as a digital array proportional to the damped, oscillating current, NMR is really more concerned with the manipulation and separation of frequencies in the radiofrequency range (10 – 1,000 MHz). The relation between magnetic field and resonance frequency is given by the Larmor equation. Different frequencies observed with MR spectroscopy (MRS) typically correspond to different chemical groups in various molecules in which the chemical shielding constant is slightly different, whereas different frequencies in MR imaging (MRI) correspond to different spatial positions. Spatial variations in the amplitude of the magnetic field (i.e. magnetic field inhomogeneity) are synonymous to spatial variations in the Larmor resonance frequency. As NMR signal is always acquired from a macroscopic volume, spatial variations in frequency will lead to line broadening in MRS. Glutamate and glutamine are two important metabolites that can be detected by proton MRS in vivo. The glutamate and glutamine H4 protons at 7 T are separated by 30 Hz. Therefore, in order to separately detect glutamate from glutamine the magnetic field homogeneity needs to be much better than 30 Hz, which corresponds to 0.1 parts-per-million at the 7 T proton Larmor frequency of 298 MHz. For MRI, magnetic field inhomogeneity leads to spatial displacement and signal loss. And while the requirements on the magnetic field homogeneity are somewhat less than for MRS, the desired magnetic field inhomogeneity is still less than 1 ppm. An infinitely long solenoidal magnet without manufacturing errors generates a perfectly homogeneous magnetic field within the magnet. However, practical magnets have a limited length and come with minor manufacturing errors, like non-uniform current density due to incorrect wire placement. As a result, the bare magnetic field can have a magnetic field inhomogeneity of > 20 ppm. Because the bare magnet field inhomogeneity is constant and typically very low order and smooth, it can almost always be readily removed by shimming as explained below. The magnetic field inhomogeneity that is most detrimental for the majority of MR studies originates from the sample itself. When a sphere of water is placed within a perfectly homogeneous magnetic field (Fig. 1C), the magnetic field outside the sphere is heavily distorted (Fig. 1D). Due to the spherical geometry the magnetic field inside the sphere is still perfectly homogeneous and therefore the NMR signal coming from the water protons is very narrow. When the same water-filled sphere is replaced with one containing a smaller air-filled sphere (Fig. 1E) the magnetic field homogeneity inside and outside the sample is heavily compromised (Fig. 1F). The water protons will experience a wide range of magnetic fields and as a result the water NMR signal will be very broad. Even though the example given in Fig. 1 appears artificial, it is in fact a very common scenario in vivo. Air cavities surrounded by water/tissue are encountered throughout the mammalian body. Prime examples are the nasal and auditory cavities in the head and lungs, intestines and bladder in the body. Fig. 2 shows a typical example of the human head at 4 T. It can be seen that areas of high magnetic field inhomogeneity are close to areas with water-air boundaries. The increased magnetic field inhomogeneity has little effect on spin-echo MR images (B), but is detrimental to gradient-echo (C) and echo-planar images (D).Static spherical harmonics shimming
Magnetic field inhomogeneity is most commonly dealt with by superimposing additional, spatially varying magnetic fields in order to counteract the inhomogeneity in the main magnetic field. While there are many magnetic fields with a well-defined spatial variation applicable to the problem at hand, magnetic fields based on spherical harmonics (SH) have been the gold standard in NMR since the introduction by Golay (1) and the formalization by Romeo and Hoult (2). There are a number of important reasons why SH-based shimming is still the gold standard even today. Firstly, spherical harmonic magnetic fields are readily generated by relatively simple coil geometries. Secondly, spherical harmonic fields are, in principle, orthogonal such that the various SH terms can be adjusted sequentially and non-iteratively. Thirdly, any magnetic field inhomogeneity can be expanded into an infinite series of SH fields such that, at least theoretically, any magnetic field disturbance can be compensated. SH shimming has been enormously successful in high-resolution NMR on well-defined and well-shaped NMR tubes as well as for small, 3D localized volumes in vivo. For 3D localized volumes a non-iterative shimming procedure (FASTMAP) was developed to quantitatively determine the required shims in the span of about 1 minute (3). First- and second-order SH fields are typically sufficient to adequately homogenize the magnetic field across 3D localized volumes in the human brain of up to 3 x 3 x 3 = 27 mL. For larger volumes, 2D slices or even entire 3D organs the magnetic field variations can typically not be adequately described by second-order SH fields (e.g. Fig. 2). In principle the magnetic field inhomogeneity can be approximated better with the inclusion of higher-order SH fields. However, limited magnet bore space and reduced efficiency of higher-order SH shims have limited the extension of SH shimming to fourth/fifth-order SH fields (4). While higher-order SH shimming provides good magnetic field homogeneity in the majority of 2D slices through the human brain, it falls short in areas of extreme magnetic field inhomogeneity such as those surrounding the nasal and auditory cavities (e.g. Fig. 2).Dynamic spherical harmonics shimming
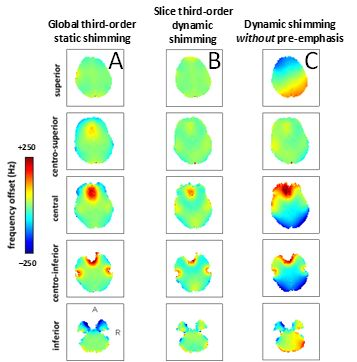
It is well-known from MRS that the required SH shim order required for adequate magnetic field homogeneity decreases with decreasing voxel size. A similar observation can be made in MRI where the SH shim order necessary to shim a 2D slice is lower than that required to shim an entire 3D volume. These observations can lead to improved magnetic field homogeneity across slices if the SH shims can be optimized on a per-slice basis. For a multi-slice MRI sequence this would lead to the requirement that SH shims need to be dynamically updated. Dynamic shim updating (DSU) was already proposed in 1996 (5,6) for linear shims, but gained more popularity with the inclusion of higher order shims, the increased need of improved shimming at higher magnetic fields and the availability of commercial DSU units (7-9). Fig. 3 shows a typical result of the improvement in magnetic field homogeneity that dynamic SH shimming can achieve over conventional, static SH shimming. As dynamic shimming relies on the ability of changing the shim settings on a per-slice basis, the abrupt changes in shim amplitudes will lead to eddy currents similar to those observed with linear field gradients. The results in Fig. 3B were only attainable after all zero-through-third order SH shims were properly pre-emphasized, including higher-to-lower-order SH cross term pre-emphasis. A total of 41 pre-emphasis and B0 correction terms were necessary for a complete compensation of unwanted eddy currents (9). Fig. 3C shows the results for dynamic shimming without pre-emphasis. It follows that full shim pre-emphasis is an absolute requirement for successful dynamic shimming. While dynamic SH shimming maximizes the performance of the available (low-order) SH shim terms, the magnetic field homogeneity is typically still less than ideal because the magnetic field homogeneity across a 2D slice exceeds the available SH terms. While dynamic SH shimming with higher SH terms (4th and higher) is technically possible the required pre-emphasis matrix would quickly become unmanageable.Moving beyond spherical harmonics
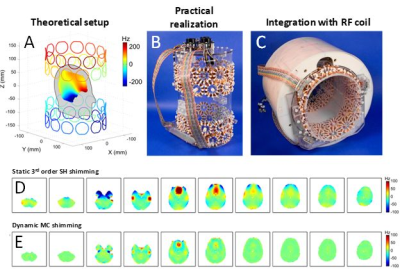
To address the shortcomings of low-order SH shimming to homogenize the human brain a large number of methods have been developed that step outside the SH framework. Placement of passive shim materials in the mouth or surrounding the human head have been reported (10-12). While passive shims can improve the magnetic field homogeneity across limited spatial regions (e.g. the frontal cortex) they typically cannot achieve whole-brain coverage. More importantly, passive shims do not have the flexibility to deal with significant intersubject variations in the magnetic field homogeneity. Small electromagnetic coils placed inside the mouth can potentially deal with the intersubject variations, but lack the spatial coverage to provide high magnetic field homogeneity across the entire brain (13). A generally applicable and arguably the most successful method is the so-called multi-coil (MC) shimming method (14-20) in which multiple, generic DC coils are placed around the subjects head (Fig. 4A). Each coil is connected to an independent amplifier capable of delivering +/- 1A current. The theoretical model of Fig. 4A was transformed into a practical setup as shown in Figs. 4B/C. Following a one-time calibration of all 48 DC coils, the magnetic field homogeneity in the human head could be improved to levels greatly exceeding that of conventional, static third-order shimming (Figs. 4D/E). Because the DC coils do not generate any measurable eddy currents MC shimming can take immediate advantage of the intrinsic benefits of dynamically updating the shim currents in a slice-specific manner (Fig. 4E). The MC shimming approach is very generic and as such it can be readily optimized for the problem at hand. Even though MC shimming has focused on the animal and human head, it is anticipated that MC shimming can provide improved performance in breast, spine and abdominal magnetic field homogeneity. Optimizing the magnetic field homogeneity is still a very active research area and recent reports have focused on combining RF and MC coils (21,22) and allowing dynamic switching of a wire network (23). However, whereas MC shimming has already been proven experimentally on mouse (16), rat (19) and human brain (17,20), many other methods are still at the simulation/proof-of-principle stage and their ultimate utility remains to be proven.Acknowledgements
No acknowledgement found.References
1. Golay MJE. Field Homogenizing coils for nuclear spin resonance instrumentation. Rev Sci Instrum 1958;29:313-315.
2. Romeo F, Hoult DI. Magnet field profiling: analysis and correcting coil design. Magn Reson Med 1984;1:44-65.
3. Gruetter R. Automatic, localized in vivo adjustment of all first- and second-order shim coils. Magn Reson Med 1993;29:804-811.
4. Pan JW, Lo KM, Hetherington HP. Role of very high order and degree B0 shimming for spectroscopic imaging of the human brain at 7 Tesla. Magn Reson Med 2013;68:1007-1017.
5. Blamire AM, Rothman DL, Nixon T. Dynamic shim updating: a new approach towards optimized whole brain shimming. Magn Reson Med 1996;36:159-165.
6. Morrell G, Spielman D. Dynamic shimming for multi-slice magnetic resonance imaging. Magn Reson Med 1997;38:477-483.
7. de Graaf RA, Brown PB, McIntyre S, Rothman DL, Nixon TW. Dynamic shim updating (DSU) for multislice signal acquisition. Magn Reson Med 2003;49:409-416.
8. Koch KM, McIntyre S, Nixon TW, Rothman DL, de Graaf RA. Dynamic shim updating on the human brain. J Magn Reson 2006;180:286-296.
9. Juchem C, Nixon TW, Diduch P, Rothman DL, Starewicz P, de Graaf RA. Dynamic shimming of the human brain at 7 Tesla. Concepts Magn Reson B 2010;37:116-128.
10. Wilson JL, Jenkinson M, Jezzard P. Optimization of static field homogeneity in human brain using diamagnetic passive shims. Magn Reson Med 2002;48:906-914.
11. Wilson JL, Jenkinson M, Jezzard P. Protocol to determine the optimal intraoral passive shim for minimisation of susceptibility artifact in human inferior frontal cortex. Neuroimage 2003;19:1802-1811.
12. Jesmanowicz A, Roopchansingh V, Cox RW, Starewicz P, Punchard WFB, Hyde JS. Local ferroshims using office copier toner. Proc Int Soc Magn Reson Med 2001;9:617.
13. Hsu JJ, Glover GH. Mitigation of susceptibility-induced signal loss in neuroimaging using localized shim coils. Magn Reson Med 2005;53:243.
14. Juchem C, Nixon TW, McIntyre S, Rothman DL, de Graaf RA. Magnetic field homogenization of the human prefrontal cortex with a set of localized electrical coils. Magn Reson Med 2010;63:171-180.
15. Juchem C, Nixon TW, McIntyre S, Rothman DL, de Graaf RA. Magnetic field modeling with a set of individual localized coils. J Magn Reson 2010;204:281-289.
16. Juchem C, Brown PB, Nixon TW, McIntyre S, Rothman DL, de Graaf RA. Multicoil shimming of the mouse brain. Magn Reson Med 2011;66:893-900.
17. Juchem C, Nixon TW, McIntyre S, Boer VO, Rothman DL, de Graaf RA. Dynamic multi-coil shimming of the human brain at 7T. J Magn Reson 2011;212:280-288.
18. Juchem C, Green D, de Graaf RA. Multi-coil magnetic field modeling. J Magn Reson 2013;236:95-104.
19. Juchem C, Herman P, Sanganahalli BG, Brown PB, McIntyre S, Nixon TW, Green D, Hyder F, de Graaf RA. DYNAmic Multi-coIl TEchnique (DYNAMITE) shimming of the rat brain at 11.7 T. NMR Biomed 2014;27:897-906.
20. Juchem C, Umesh Rudrapatna S, Nixon TW, de Graaf RA. Dynamic multi-coil technique (DYNAMITE) shimming for echo-planar imaging of the human brain at 7 Tesla. Neuroimage 2015;105:462-472.
21. Han H, Song AW, Truong TK. Integrated parallel reception, excitation, and shimming (iPRES). Magn Reson Med 2013;70:241-247.
22. Stockmann JP, Witzel T, Keil B, Polimeni JR, Mareyam A, LaPierre C, Setsompop K, Wald LL. A 32-channel combined RF and B0 shim array for 3T brain imaging. Magn Reson Med 2016;75:441-451.
23. Harris CT, Handler WB, Chronik BA. A new approach to shimming: The dynamically controlled adaptive current network. Magn Reson Med 2014;71:859-869.
Figures