Cardiac DTI: Acquisition Techniques
Christian Stoeck1

1University and ETH Zurich, Switzerland

Synopsis

The two most commonly used approaches to overcome motion induced signal dephasing in cardiac diffusion weighted imaging rely on stimulated echo acquisition mode and motion compensated spin echo diffusion weighted imaging. Both sequences employ different strategies to generate diffusion contrast. In recent in-vivo imaging as well as Monte Carlo simulations it has become apparent that the quantitative parameters such as mean diffusivity and fractional anisotropy substantially differ between the two imaging approaches. The aim of this educational is to explain motion compensation strategies and discuss the resulting differences in measurements.

Introduction

When talking about microstructural imaging by means of diffusion tensor imaging, q-ball imaging, diffusion spectrum imaging or even the assessment of organ perfusion by intra voxel incoherent motion, common ground is found by diffusion weighted imaging: a method to sensitize the applied MR-sequence to random motion of water molecules. Diffusion sensitizing by pulsed field gradients dates back to 1965 when Stejskal and Tanner incorporated a pair of field gradients into a spin echo sequence (1). Ever since, diffusion weighting has been applied to almost every organ in the human body. Application to the heart however faces challenges of organ motion. The aim of this educational is to elucidate how we can measure molecular water displacement in the micrometre range inside an organ that moves on the order of centimetres. The two most commonly used approaches are explained and differences in measurement results discussed.

Diffusion encoding in the beating heart

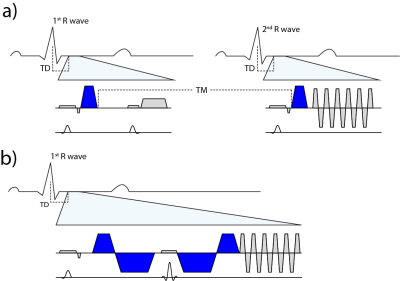
To address the challenge of cardiac motion in a diffusion weighted imaging experiment, one needs to design a filter sensitive to a random walk, but insensitive to myocardial motion. This can be achieved by a dedicated cardiac MR (CMR) sequence design during acquisition or during post processing. Herein we will focus on the two most commonly used approaches of filtering cardiac motion during the acquisition (figure 1).

The first attempts were based on a Stimulated Echo Acquisition Mode (STEAM) sequence (2,3). This approach relies on splitting the modulation and demodulation part of a STEAM sequences across two consecutive heart beats (figure 2a). By doing so, periodic motion such as cardiac contraction is filtered from random motion of water diffusion. It is therefore crucial, that the periodicity constraint is valid, meaning that each material point follows the same trajectory during two consecutive heart beats. A mismatch in motion states will inevitably lead to signal dephasing (4).

A more SNR efficient alternative to STEAM (5) is based on Spin echo sequences. To understand its functionality it is necessary to examine the phase evolution of magnetization moving through a temporal varying gradient waveform. The Taylor expansion of the motion trajectory comes in handy by parameterizing the water molecule’s phase in terms of gradient moments. A conventional Stejskal Tanner encoding scheme rephases stationary magnetization by nulling the zeroth gradient moment. Nulling higher order moments (6–9) allows for imaging during contractile motion without cardiac motion induced signal dephasing (figure 2b). E.g. in second order motion compensated diffusion encoding, material points have to follow a motion trajectory that is defined by an initial position, velocity and acceleration. Any deviation from such a trajectory, e.g. due to jerk components, during the application of diffusion encoding gradients, will lead to phase accumulation and potential signal dephasing. It is pivotal to keep the waveform duration of motion compensated diffusion gradients as short as possible. This can be achieved by applying convex optimization during waveform construction (10) and the use of high performance hardware.

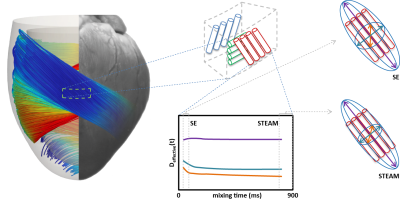
Having mastered diffusion weighted imaging in the beating heart one can now derive parameters characterizing tissue properties. Due to the limited amount of time in an in-vivo setting, diffusion tensor imaging (11) is commonly employed, demanding a certain diffusion weighting and number (6 at least) of diffusion encoding directions (12). From the diffusion tensor, scalar parameters are derived such as the mean diffusivity and fractional anisotropy. Additionally, the principal myofiber orientation and sheetlet alignment (figure 3) can be computed.

When measuring diffusivities inside the myocardium, it has become evident that the two sequences do not provide the same results (13,14). Comparing both sequences reveals fundamental differences in their design:

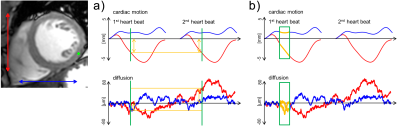
1) Unlike in homogeneous media the diffusivity D in non-homogeneous media such as the myocardium is time dependent, and only in the limit of long mixing times (TM) the measured diffusivity D(TM) converges to a constant Dꝏ < D0. At this point the underlying medium (i.e. diffusing liquid, diffusion restrictions, different diffusion compartments) is homogenised to an “effective medium” a process also known as “coarse graining” (15). For the STEAM sequence TM is fixed to the time between two consecutive heart-beats (on the order of 1s), while for SE imaging diffusion sensitivity of the sequences is limited to 40-60ms. From measurements in ex-vivo hearts it has been shown that coarse graining over the structures found in a heart has taken place for mixing times encountered in cardiac STEAM imaging (16) (figure 3). For the timescale usually encountered in SE imaging a time dependency of D was found suggesting non-Gaussian diffusion.

2) For cardiac STEAM DWI the diffusion encoding gradients are about two orders of magnitude shorter compared to the TM, which allows for using the narrow pulse assumption. This implies that the phase resulting from a random walk is linked to the effective displacement of the water molecule (end-position – start-position). In contrast the SE approach relies on keeping the diffusion encoding gradients switched on during most of the time. As described in the review article by Kiselev (17) the resulting signal is dependent on the correlation function of the particles velocity along the diffused path instead of their displacement only. This correlation function depends on the underlying structure and permeability of diffusion boundaries. Since the myocardium is of disordered structure, i.e. cardiomyocytes do not have the exact same size, packing and alignment finding an analytical representation is challenging. Monte Carlo simulations of the diffusion process in the myocardial based on histologically derived microstructure (18) has shown great potential in investigating the origin in variation of the measured values such as diffusivities and fractional anisotropies due to changes in structure and sequence used.

Conclusion

Currently, STEAM and motion compensated spin echo techniques are most frequently used when generating diffusion contrast in the beating heart. While scalar parameter such as mean diffusivity and fractional anisotropy correlate with pathological findings, it is important to understand that the resulting quantitative values depend not only on the underlying microstructure, but also on the sequence parameters such as encoding duration, gradient strength and gradient waveform.

Acknowledgements

No acknowledgement found.

References

1. Stejskal EO, Tanner JE. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient. J. Chem. Phys. 1965;42:288. doi: 10.1063/1.1695690.

2. Edelman RR, Gaa J, Wedeen VJ, Loh E, Hare JM, Prasad P, Li W. In vivo measurement of water diffusion in the human heart. Magn. Reson. Med. 1994;32:423–8.

3. Reese TG, Weisskoff RM, Smith RN, Rosen BR, Dinsmore RE, Wedeen VJ. Imaging myocardial fiber architecture in vivo with magnetic resonance. Magn. Reson. Med. 1995;34:786–91.

4. Reese TG, Wedeen VJ, Weisskoff RM. Measuring Diffusion in the Presence of Material Strain. J. Magn. Reson. Ser. B 1996;112:253–258.

5. von Deuster C, Stoeck CT, Genet M, Atkinson D, Kozerke S. Spin echo versus stimulated echo diffusion tensor imaging of the in vivo human heart. Magn. Reson. Med. 2016;76:862–872. doi: 10.1002/mrm.25998.

6. Pipe JG, Chenevert TL. A progressive gradient moment nulling design technique. Magn. Reson. Med. 1991;19:175–9.

7. Gamper U, Boesiger P, Kozerke S. Diffusion imaging of the in vivo heart using spin echoes--considerations on bulk motion sensitivity. Magn. Reson. Med. 2007;57:331–7. doi: 10.1002/mrm.21127.

8. Stoeck CT, von Deuster C, Genet M, Atkinson D, Kozerke S. Second-order motion-compensated spin echo diffusion tensor imaging of the human heart. Magn. Reson. Med. 2015;000:n/a-n/a. doi: 10.1002/mrm.25784.

9. Welsh C, Di Bella E, Hsu E. Higher-Order Motion-Compensation for In Vivo Cardiac Diffusion Tensor Imaging in Rats. IEEE Trans. Med. Imaging 2015;0062:1–1. doi: 10.1109/TMI.2015.2411571.

10. Aliotta E, Wu HH, Ennis DB. Convex optimized diffusion encoding (CODE) gradient waveforms for minimum echo time and bulk motion-compensated diffusion-weighted MRI. Magn. Reson. Med. 2016;00:n/a-n/a. doi: 10.1002/mrm.26166.

11. Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys. J. 1994;66:259–67. doi: 10.1016/S0006-3495(94)80775-1.

12. Froeling M, Nederveen AJ, Nicolay K, Strijkers GJ. DTI of human skeletal muscle: the effects of diffusion encoding parameters, signal-to-noise ratio and T2 on tensor indices and fiber tracts. NMR Biomed. 2013;26:1339–52. doi: 10.1002/nbm.2959.

13. von Deuster C, Stoeck CT, Genet M, Atkinson D, Kozerke S. Spin echo versus stimulated echo diffusion tensor imaging of the in vivo human heart. Magn. Reson. Med. 2016;76. doi: 10.1002/mrm.25998.

14. Scott AD, Nielles-Vallespin S, Ferreira PF, Khalique Z, Gatehouse PD, Kilner P, Pennell DJ, Firmin DN. An in-vivo comparison of stimulated-echo and motion compensated spin-echo sequences for 3 T diffusion tensor cardiovascular magnetic resonance at multiple cardiac phases. J. Cardiovasc. Magn. Reson. 2018;20:1–15. doi: 10.1186/s12968-017-0425-8.

15. Novikov DS, Fieremans E, Jespersen SN, Kiselev VG. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. NMR Biomed. 2018:1–53. doi: 10.1002/nbm.3998.

16. Kim S, Chi-Fishman G, Barnett AS, Pierpaoli C. Dependence on diffusion time of apparent diffusion tensor of ex vivo calf tongue and heart. Magn. Reson. Med. 2005;54:1387–96. doi: 10.1002/mrm.20676.

17. Kiselev VG. Fundamentals of diffusion MRI physics. NMR Biomed. 2017;30:1–18. doi: 10.1002/nbm.3602.

18. Rose JN, Nielles-Vallespin S, Ferreira PF, Firmin DN, Scott AD, Pennell DJ. Novel insights into in‐vivo diffusion tensor cardiovascular magnetic resonance using computational modeling and a histology‐based virtual microstructure. Soc. Cardiovasc. Magn. Reson. Annu. Meet. 2018:373719. doi: 10.1002/mrm.27561.

Figures

Figure 1 a) Stimulated Echo Acquisition Mode sequence and b) second order motion compensated spin echo sequence for cardiac diffusion weighted imaging. TD: trigger delay, TM: mixing time

Figure 2 top row: cardiac motion from a tracked region of interest (green square in the inferno lateral wall) projected onto two diffusion encoding directions (red/blue), bottom row: random walk projected onto the same two orthogonal diffusion encoding directions. a) for STEAM imaging a spatial position is encoded quasi instantaneously (green line). Periodicity of cardiac motion is required to avoid motion induced dephasing. b) for spin echo imaging second order motion compensated diffusion encoding gradients are switched on (green box) in order to filter low order cardiac motion. Diffusion corresponds to a random path and will lead to a phase dispersion and hence signal attenuation.

Figure 3 The predominant orientation of cardiomyocytes forms a double helical structure, while multiple myocytes are bundled into what have become known as sheetlet. In non-homogeneous media the diffusivity is (mixing) time dependent. The myocardium constitutes such a non-homogeneous medium with additional anisotropy, leading to different time dependencies of D when measuring along the principal myocyte direction (purple), along the principal sheetlet orientation (blue) or orthogonal to the sheetlets (orange) (figure adopted from (16)). Spin echo (SE) and stimulated echo acquisition mode (STEAM) based imaging techniques apply unequal diffusion sensitizing strategies at different timescales, hence the resulting apparent diffusivities differ.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)