Efficient & Effective Numerical Simulations for RF Coil Modeling & Safety Prediction
1C.J. Gorter Center for High-Field MRI, Radiology, Leiden University Medical Center, Leiden, Netherlands
Synopsis
This educational talk is tailored to the efficient and effective use of numerical simulation techniques for the assessment of safety and effectiveness of RF coil designs. Proper modeling practices will be identified, and recently developed methodologies will be discussed.
Purpose
Numerical EM simulations have come to play an indispensable role in RF coil design and RF safety assessments (1). The widespread accessibility of various full-wave numerical methods in combination with the growing demands in terms of problem complexity, continues to present us with the challenge of choosing the most effective strategy. Whereas the numerical verification (e.g. comparison to an analytical solution) has typically been demonstrated in literature, the accuracy of the obtained results will still strongly depend on the specific problem properties and on the relevant quantities of interest. It is therefore our task to secure the predictive value when using these tools in an efficient manner.Background
In this educational talk we will briefly identify the key properties of some of the most common full-wave numerical methods, such as the finite difference time domain (FDTD) method, finite element method (FEM) and methods based on integral equations (IE) (2). Among the most popular is FDTD due to its memory efficiency when handling complex heterogeneous body models, whereas FEM can handle a large range in spatial scales which makes FEM very suited in modeling fine structures such as implants. Recently, the application of the volume integral equation method in handling anatomical models has regained interest, yielding results comparable to FDTD (3). Regarding the differences between these solution methods, it is important to consider their advantages and drawbacks when selecting the most appropriate tool for the various scenarios relevant to MRI.Numerical and experimental validation
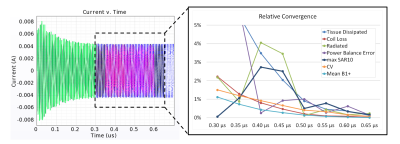
Regardless of the numerical method used, it is important to assess the sensitivity of the numerical result both as a function of model parameters or simplifications as well as solver settings such as spatial resolution and convergence tolerance. A useful metric in this context is the power balance which tests the obtained field solution on energy conservation principles (4). A basic example of such an assessment in a resonant 3T body coil is shown in Figure 1, where the convergence of different quantities of interest is determined for a different number of time-steps using FDTD.
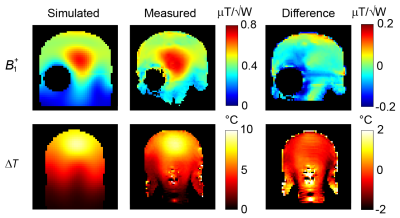
Ultimately, experimental validation is vital for assuring that all relevant physical interactions are adequately represented in the model. This should involve mapping of the B- and preferably also E-fields using a reference phantom (5,6), and account for RF chain losses between the scanner’s power reference plane and the coil plug to enable a quantitative comparison. An example of such a validation is shown in Figure 2, where an RF coil model was validated using B1+ mapping and MR thermometry (which relates to the E-field) in a head-sized phantom at 7T (7).
Circuit co-simulation
A useful procedure for tuning a resonant RF coil model is to de-embed the lumped elements from the numerical grid, and move these to a circuit-level representation of the RF coil (8–10). This requires the 3D field responses for each of the lumped element positions to be computed once, after which the solution for arbitrary values of the lumped elements can be obtained almost instantly in a post-processing step. This can be particularly useful in the design and optimization of RF coils with multiple transmit channels and complex coupling behaviour (11).Model order reduction
In most RF simulation studies a generic anatomical body model is used to study different coil designs or safety aspects. In (12) this aspect is exploited to accelerate RF coil simulations by characterizing the electrodynamic response of the body model during an off-line stage, and interfacing this response to the computational domain of the RF coil, which can be handled much more efficiently using surface integral equations. This two-way link enabled accelerations up to 500-fold with negligible loss in accuracy, allowing RF coil models to be simulated in a matter of minutes.
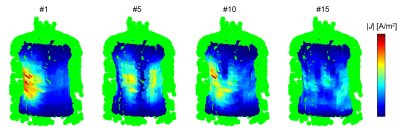
Another example of model order reduction which lives on the typically fixed properties of the anatomical model has been demonstrated in modeling dielectric shimming materials (13). In this approach, the 3D field response of the spatial domain which can contain the dielectric shim is characterized in advance. The unknown currents induced in this domain are then solved after projecting the problem onto a reduced order basis, resembling electric current “modes” as illustrated in Fig. 3. By doing so, simulations of high permittivity pads were accelerated to under a second per configuration.
Conclusion
Numerical simulations offer versatile tools which continue to play a central role in RF coil engineering and RF safety assessments. Efficient and effective application of these tools enables current and upcoming MR technologies to reach their full potential.Acknowledgements
No acknowledgement found.References
1. Fiedler TM, Ladd ME, Bitz AK. SAR Simulations & Safety. Neuroimage 2017. doi: 10.1016/j.neuroimage.2017.03.035.
2. Jin J-M. Electromagnetic analysis and design in magnetic resonance imaging. CRC Press; 1998.
3. Polimeridis AG, Villena JF, Daniel L, White JK. Stable FFT-JVIE solvers for fast analysis of highly inhomogeneous dielectric objects. J Comput Phys 2014;269:280–296. doi: 10.1016/J.JCP.2014.03.026.
4. Kuehne A, Goluch S, Waxmann P, Seifert F, Ittermann B, Moser E, Laistler E. Power balance and loss mechanism analysis in RF transmit coil arrays. Magn Reson Med 2015;74:1165–1176. doi: 10.1002/mrm.25493.
5. Hoffmann J, Henning A, Giapitzakis IA, Scheffler K, Shajan G, Pohmann R, Avdievich NI. Safety testing and operational procedures for self-developed radiofrequency coils. NMR Biomed 2016;29:1131–1144. doi: 10.1002/nbm.3290.
6. Bitz AK, Kraff O, Orzada S, Maderwald S, Brote I, Johst S, Ladd ME. Assessment of RF Safety of Tx Coils at 7 Tesla by Experimental and Numerical Procedures. In: Proceedings of the 19th Annual Meeting ISMRM, Montreal, QC, Canada, 2011. p. 490.
7. Brink WM, Wu Z, Webb AG. A Simple Head-sized Phantom for Realistic Static and Radiofrequency Characterization at High Fields. Magn Reson Med 2018.
8. Kozlov M, Turner R. Fast MRI coil analysis based on 3-D electromagnetic and RF circuit co-simulation. J Magn Reson 2009;200:147–152. doi: 10.1016/j.jmr.2009.06.005.
9. Lemdiasov RA, Obi AA, Ludwig R. A Numerical Postprocessing Procedure for Analyzing Radio Frequency MRI Coils. Concepts Magn Reson Part A 2011;38:133–147. doi: 10.1002/cmr.a.
10. Paška J, Froehlich J, Brunner DO, Pruessmann KP, Vahldieck R. Field superposition method for RF coil design. In: Proceedings of the 17th Annual Meeting of ISMRM, Honolulu, Hawaii, USA, 2009. p. Proc Int Soc Magn Reson Med 17.
11. Beqiri A, Hand JW, Hajnal J V., Malik SJ. Comparison between simulated decoupling regimes for specific absorption rate prediction in parallel transmit MRI. Magn Reson Med 2015;74:1423–1434. doi: 10.1002/mrm.25504.
12. Villena JF, Polimeridis AG, Eryaman Y, Adalsteinsson E, Wald LL, White JK, Daniel L. Fast Electromagnetic Analysis of MRI Transmit RF Coils Based on Accelerated Integral Equation Methods. IEEE Trans Biomed Eng 2016;63:2250–2261. doi: 10.1109/TBME.2016.2521166.
13. van Gemert JHF, Brink WM, Webb AG, Remis RF. High-Permittivity Pad Design for Dielectric Shimming in Magnetic Resonance Imaging using Projection Based Model Reduction and a Nonlinear Optimization Scheme. IEEE Trans Med Imaging 2018. doi: 10.1109/TMI.2018.2791179.
Figures