4779

Automating fetal brain reconstruction using distance regression learning

Lucilio Cordero-Grande¹, Anthony N Price¹, Emer J Hughes², Robert Wright³, Mary A Rutherford², and Joseph V Hajnal¹

¹Centre for the Developing Brain and Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, ²Centre for the Developing Brain, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, ³Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom

Synopsis

We describe a method for automated fetal brain reconstruction from stacks of 2D single-shot slices. Brain localization is performed by a deep distance regression network. Slice alignment is accomplished by a global search in the rigid transform space followed by registration using a fractional derivative metric. An outlier robust hybrid $1,2$ -norm and linear high order regularization are used for reconstruction. Brain localization has achieved competitive results without requiring annotated segmentations. The method has produced acceptable reconstructions in 129 out of 133 3T fetal examinations tested so far.

Introduction

Reconstruction of structural fetal brain MRI from arbitrarily oriented slice stacks¹ has to consider unpredictable fetal motion, spin history, thick slices and/or low SNR, and intensity inhomogeneities^2,3. Most approaches require a brain segmentation to constrain rigid registration, which traditionally implied some manual supervision. By training deep neural architectures, there’s growing evidence that robust reconstructions can be produced without human intervention^4,5. However, existing proposals require slicewise brain delineation in a set of training stacks and are based on 2D architectures, which may not fully exploit contextual information in the labelled data⁶. We propose to train a V-net⁷ to regress a distance transform to the fetal brain using only annotations of its bounding box (BB) and show its utility in constraining the alignment during reconstruction.

Methods

Localization is performed on each acquired stack by training a deep V-net with the cost in Fig. 1(1), where $p$ at voxel $n$ is given in Fig. 1(2). $3$ x $3$ x $1$ within-slice convolutions are stacked with $1$ x $1$ x $3$ through-plane convolutions. Two encoding, one connection and one decoding level are used, each of them comprised of residual blocks⁸. Joint max-average pooling doubles the channel number at coarser scales. Stack reconstructions are preprocessed by $2$ x in-plane downsampling, largest average intensity slice selection from $4$ -slice neighborhoods, and channel concatenation of blocks of $2$ x $2$ neighboring in-plane pixels. Brain BB were marked in $256$ stacks from $45$ participants from which two $128$ / $128$ training/testing sets are generated for two independent performance experiments and later combined to train the network for reconstruction. Each stack is $50$ x augmented by applying both global and per-slice random translations, rotations and multiplicative biases. Ellipsoidal distance transforms are used to train the network ( $30$ min/ $128$ stacks), from which regressed distances can fit per-stack brain localization ellipsoids.

Stack information is modelled by the encoding operator $\mathbf{E}$ in Fig. 1(3). Soft masks and stack data $\mathbf{y}$ are back transformed by $\mathbf{E}_v^H$ , with $v$ the stack index and centroid-aligned to perform wide range translational and rotational tracking by brute-force search in a discretized rigid transform space. Reconstructions are obtained at $2$ mm and $1$ mm by solving Fig. 1(4) using iteratively re-weighted conjugate gradient. Masks are propagated backwards and forwards following Fig. 1(5). Reconstruction is interleaved with alignment refinement by a Levenberg-Marquardt optimization of Fig. 1(6) operating successively at the stack, package and excitation levels with most steps at $2$ mm. Rotation to a standard pose employs a spatial transformer network⁹.

Supine scans on a a Philips 3T Achieva with a $32$ -channel cardiac coil from a cohort of $141$ fetuses ( $21$ - $38$ weeks GA) with full examination (minimum of $6$ stacks) in $133$ of them are used for testing. The protocol uses the MB tip-back prepared zoom TSE technique¹⁰. Data is acquired at $1.1$ x $1.1$ x $2.2$ mm with $TR=2.2$ s, $TE=250$ ms, MB $2$ , SENSE $2$ half-scan $0.65$ (approximately $2$ min per stack), reconstructed using hybrid-space SENSE¹¹, and inhomogeneity-corrected using $B_1$ calibrations.

Results

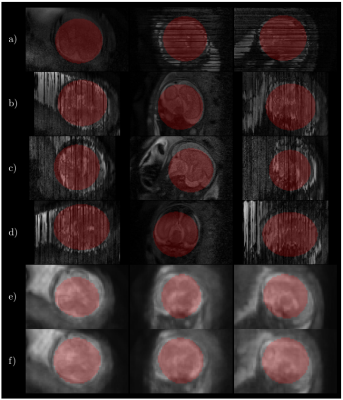
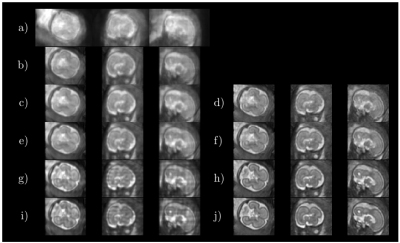
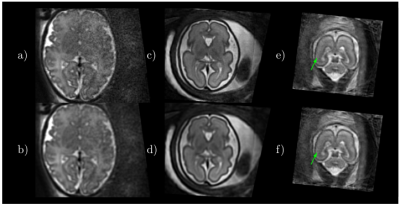
Fig. 2 shows some quantitative results on localization when using a distance transform regressor versus an equivalent semantic segmentation approach, together with the results reported in⁵. In Fig. 3 the detected ellipsoids are overlaid onto the original stacks and

$\mathbf{E}^H\mathbf{y}$ before and after ellipsoid alignment. Fig. 4 shows different alignment stages at

$2$ mm, both for

$\mathbf{E}^H\mathbf{y}$ and the reconstructed images. Fig. 5 compares the results with and without the outlier-robust norm and provide reconstructions optimally balanced for SNR or resolution. Visual inspection has revealed

$129$ /

$133$ meaningful reconstructions.

Discussion

Comparisons with recent literature⁵ show that our method seems to offer competitive localization performance at a lower computational cost and without using labelled segmentations, although further comparisons should harmonize the experimental conditions. On-going tests try to elucidate the differences between distance and segmentation based learning, as marginal benefits in favor of the former (Fig. 2) are not yet conclusive. Brain localization can cope with degradation in the original stacks (Fig. 3), with drastic misalignments observed only for severely cropped brains. Good alignment is observed using the proposed metric and detected mask propagation (Fig. 4). Hybrid

$q,2$ -norm reconstruction copes with artifacted slices and high order linear regularization provides minimal suppression of high spatial frequency harmonics (Fig. 5) without introducing artifacts at low SNR.

Conclusion

We have described an automatic pipeline for structural fetal brain reconstruction. Annotated segmentations used for localization training are reduced to BB annotation. Signed distance transform regression is proposed for segmentation. Slice alignment is satisfactory in the presence of moderately imperfect masking. Reconstruction copes with inconsistent slices in a parameter-free manner and with low SNR in a linear manner. The method is in use for automated fetal reconstructions in our clinical routine.

Acknowledgements

The authors acknowledge financial support from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013) / ERC Grant Agreement n.319456. This work was also supported by the Wellcome EPSRC Centre for Medical Engineering at King’s College London (WT 203148/Z/16/Z) and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.

References

1. Studholme C. Mapping fetal brain development in utero using MRI: The big bang of brain mapping. Annu Rev Biomed Eng. 2011. 13:345‐368.

2. Kuklisova-Murgasova M, Quaghebeur G, Rutherford, MA, Hajnal, JV, Schnabel, JA, Reconstruction of fetal brain MRI with intensity matching and complete outlier removal. Med Image Anal. 2012. 16:1550-1564.

3. Tourbier S, Velasco-Annis C, Taimouri V, Hagmann P, Meuli R, Warfield SK, Bach M, Gholipour A. Automated template-based brain localization and extraction for fetal brain MRI reconstruction. NeuroImage. 2017. 155:460-472.

4. Salehi SSM, Hashemi SR, Velasco-Annis C, Ouaalam A, Estroff JA, Erdogmus D, Warfield SK, Gholipour A. Real-time automatic fetal brain extraction in fetal MRI by deep learning, IEEE 15th ISBI. 2018:720-724.

5. Ebner M, Wang G, Li W, Aertsen M, Patel PA, Aughwane R, Melbourne A, Doel T, David AL, Deprest J, Ourselin S, Vercauteren T. An automated localization, segmentation and reconstruction framework for fetal brain MRI. MICCAI. 2018, LNCS 11070:313-320.

6. Naylor P, Marick L, Reyal F, Walter T. Segmentation of nuclei in histopathology images by deep regression of the distance map. IEEE Trans Med Imag. 2018, in press.

7. Milletari F, Navab N, Ahmadi SA. V-net: Fully convolutional neural networks for volumetric medical image segmentation. 4th Int Conf On 3D Vision (3DV). 2016: 565-571.

8. He K, Zhang X, Ren S, Sun J. Identity mappings in deep residual networks. ECCV 2016, part IV, LNCS 9908:630-645.

9. Wright R, Khanal B, Gomez A, Skelton E, Matthew J, Hajnal JV, Rueckert D, Schnabel JA. LSTM Spatial Co-transformer Networks for Registration of 3D Fetal US and MR Brain. PIPPI/DATRA MICCAI. 2018. LNCS 11076:149-159.

10. Price AN, Cordero-Grande L, Malik SJ, Hajnal JV. Multiband zoom TSE imaging: increasing efficiency with multiband tip-back preparation pulses. 27th ISMRM. 2018. 0062.

11. Zhu K, Dougherty RF, Wu H, Middione MJ, Takahashi AM, Zhang T, Pauly JM, Kerr AB. Hybrid-Space SENSE Reconstruction for Simultaneous Multi-Slice MRI. IEEE Trans Med Imag. 2016. 35(8):1824-1836.

Figures

Problem formulation for a) localization, b) reconstruction c) alignment.

Centroid estimate errors

$|\hat{\mathbf{c}}-\mathbf{c}|$ , intersection over union (IoU) coefficient, and per-stack computation times for distance regression and equivalent semantic segmentation. Results of the P-net method⁵, with similar number of stacks for training and testing, are provided as a reference, although they come from different datasets. IoU results are provided for

$5$ mm-dilated BBs⁵.

Brain localization examples where the ellipsoids obtained by thresholding the estimated distance maps are overlaid on the image data: a-d) Detection for different stacks of the same participant: the detection is robust to spin history, inconsistent information in the slice direction and moderately low SNR.

$\mathbf{E}^{H}\mathbf{y}$ and

$\mathbf{E}^{H}\mathbf{M}$ e) before and f) after centroid alignment. Note the improved overlap after alignment.

Alignment refinements at

$2$ mm (same subject as in Fig. 3). a)

$\mathbf{E}^{H}\mathbf{y}$ after centroid alignment, b)

$\mathbf{E}^{H}\mathbf{y}$ after translational tracking, c)

$\mathbf{E}^{H}\mathbf{y}$ and d)

$\hat{\mathbf{x}}$ after rotational tracking, e)

$\mathbf{E}^{H}\mathbf{y}$ and f)

$\hat{\mathbf{x}}$ after per-stack alignment, g)

$\mathbf{E}^{H}\mathbf{y}$ and h)

$\hat{\mathbf{x}}$ after per-package alignment, i)

$\mathbf{E}^{H}\mathbf{y}$ and j)

$\hat{\mathbf{x}}$ after per-excitation alignment. The registration is robust to moderate masking imperfections as observed in Fig. 3f.

Reconstruction results for three exemplary cases. a,b) Scan with low SNR and strong

$B_1$ shading. c,d) Good quality scan. e,f) Scan with strong spin history due to respiratory motion. a,c,e) Minimally regularized reconstruction (

$\lambda=5$ ,

$m=100$ , targeted resolution

$\sim 1.1$ mm). b,d) Reconstruction optimized for SNR (

$\lambda=75$ ,

$m=16$ , targeted resolution

$\sim 1.35$ mm). f) Reconstruction when disabling robustness to outlier slices (fixing

$q=2$ ). The regularization allows to mitigate noise -b) vs a)- but slightly blurs fine detailed structures in high quality scans -d) vs c)-. The arrow points to an area of suppressed artifacts when activating the robust formulation -e) vs f)-.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)

4779