Synopsis

Compressed sensing combined with parallel imaging has allowed significant reduction in MRI scan time. However, image reconstruction remains challenging and common methods rely on a coil calibration step. In this work, we focus on calibrationless reconstruction methods that promote group sparsity. The latter have allowed theoretical improvements in CS recovery guarantees. Here, we compare the performances of several regularization terms (group-LASSO, sparse group-LASSO and OSCAR) that define with the data consistency term the convex but nonsmooth objective function to be minimized. The same primal-dual algorithm can be used to perform this minimization. Our results demonstrate that OSCAR-based reconstruction is competitive with state-of-the-art $$$\ell_1$$$-ESPIRiT.

Introduction

Theory

General problem statement. Let $$$N$$$ , $$$L$$$ and $$$M$$$ being respectively the image resolution, the number of channels and the number of k-space measurement. We denote by $$$\pmb{y} =[ \pmb{y}_1, \ldots, \pmb{y}_L ] \in \mathbb{C}^{M \times L}$$$ the acquired k-space data and by $$$\underline{\pmb{x}}=\left[\pmb{x}_1,\ldots, \pmb{x}_L \right] \in \mathbb{C}^{N \times L}$$$ the reconstructed MR images.

The image reconstruction problem reads as follows:

$$\hat{\underline{\pmb{x}}} = \underset{\underline{\pmb{x}}\in \mathbb{C}^{N \times L}}{\text{argmin}} \left\{\frac{1}{2} \sum_{\ell = 1}^{L} \sigma^{-2}_\ell \| f_\Omega(\pmb{x}_\ell) - \pmb{y}_\ell \|_2^2 + g(T \underline{\pmb{x}})\right\}$$

where $$$f_\Omega$$$ is the forward under-sampling Fourier operator. $$$T \in \mathbb{C}^{N_\Psi \times N}$$$ is a linear operator related to a multiscale decomposition $$$ \Psi $$$ and $$$g$$$ is the joint sparsity promoting term.

Group LASSO^1,2. We define $$$\underline{\pmb{z}}=\left[ \pmb{z}_1, \ldots, \pmb{z}_L \right] \in \mathbb{C}^{N_\Psi \times L}$$$, with $$$\pmb{z}_\ell \in \mathbb{C}^{N_\Psi}$$$ the wavelet coefficients composed of $$$S$$$ sub-bands having $$$P_s$$$ coefficients each. For $$$\underline{\pmb{z}} \in \mathbb{C}^{N_\Psi \times L}$$$, the group-LASSO regularization is given by:

$$g_{\text{GL}}(\underline{\pmb{z}}) = \|\underline{\pmb{z}} \|_{1,2} = \sum_{s=1}^{S} \left( \lambda \gamma^{s_c} \sum_{p=1}^{P_s} \sqrt{ \sum_{\ell=1}^{L}\left | z_{sp\ell}\right| ^2 } \right)$$

where $$$z_{sp\ell}$$$ is the $$$p^{\text{th}}$$$ wavelet coefficient of the $$$s^{\text{th}}$$$ sub-band (in the $$$s_c$$$-scale) for the $$$\ell^{\text{th}}$$$ coil. For a given $$$s$$$ and $$$p$$$, the proximity operator of this penalty reads:

$$\left({\rm prox}_{\lambda \gamma^{s_c} \| \cdot \|_{1,2}}(\underline{\pmb{z}})\right)_{sp\ell} = \begin{cases} z_{sp\ell} \left(1 - \frac{\lambda \gamma^{s_c}}{\alpha_{sp}} \right)&, \text{if } \alpha_{sp}\geq \lambda \gamma^{s_c}\\ 0 &, \text{otherwise}\end{cases}$$

with $$$\alpha_{sp} = \sqrt{\sum_{\ell=1}^{L} |z_{sp\ell} |^2 }$$$.The hyper-parameters $$$\lambda>0$$$ and $$$\gamma>0$$$ enable a $$$s_c$$$-scale dependent regularization according to a power-law behavior⁷.

Sparse group-LASSO³. On top of inter-group sparsity, the sparse group-LASSO imposes intra-group sparsity too:

$$ \forall \underline{\pmb{z}} \in \mathbb{C}^{N_\Psi \times L}, g_{\rm sGL}(\underline{\pmb{z}}) = g_{\rm GL}(\underline{\pmb{z}}) + \mu\, \|\underline{\pmb{z}}\|_1 $$

The proximity operator of $$$g_{sGL}$$$ corresponds to the composition of the proximity operator of the group-LASSO and the soft-thresholding³.

Octogonal Shrinkage and Clustering Algorithm for Regression^4,5. Instead of using an $$$\ell_2$$$ norm to define the groups, one can infer a group structure using a pairwise $$$\ell_\infty$$$ norm while imposing the $$$\ell_1$$$ norm as a sparsity constraint. This leads to the OSCAR regularization that reads as follows:

$$\begin{align}\label{eq:oscar_penalty}g_{\rm OSCAR}(\pmb{z}) &= \sum_{s = 1}^{S}\lambda \left[ \sum_{j = 1}^{P_s L} |z_{sj}| + \gamma \sum_{j<k} \text{max}\{|z_{sj}|, |z_{sk}|\}\right]\nonumber\\ &= \sum_{s=1}^{S}\lambda\left[ \sum_{j = 1}^{P_s L} \left(\gamma(j-1)+1\right)|z_{sj}|_\downarrow\right]\end{align}$$

where $$$\underline{\pmb{z}}_\downarrow\in \mathbb{C}^{N_\Psi \times L}$$$ is the inter sub-band and channel wavelet coefficients sorted in decreasing order , i.e.: $$$\forall s \in \mathbb{N}, |z_{s1}| \leq \dots \leq|z_{sP_sL}|$$$. It's proximity operator is also explicit^4,5.

Primal-dual optimization algorithm. To solve the image reconstruction problem, we implemented the primal-dual optimization method Condat⁸-Vù⁹ summarized in Fig.1. As all these penalty terms are prox-friendy, one can use any proximal splitting¹⁰ algorithm.

Experiments & Results

Acquisition parameters. A modified 2D T2*-weighted GRE sequence¹¹ composed of 34 spokes (acceleration factor of 15 in time) and 3072 samples each (under-sampling factor of 2.5).The acquisition parameter were set as follows:$$$\text{ FOV} = 200 \times 200 \text{mm}^2$$$, slice thickenss $$$= 3mm$$$, $$$ \text{TR}= 550 \text{ms}$$$ (for 11 slices), $$$\text{TE}=30\text{ms}$$$, =$$$\text{ BW}100 \text{kHz}$$$ and $$$\text{FA}=25^\circ$$$.

Reconstruction parameters. All hyper-parameters were set using a grid-search procedure and the undecimated bi-Orthogonal wavelet transform with 4 decomposition scales was used. We compared the Sum-Of-Squares for the gLASSO, sgLASSO and OSCAR regularizations.

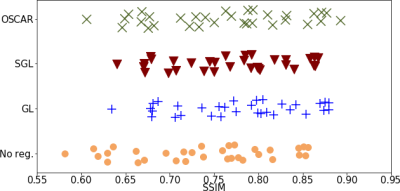
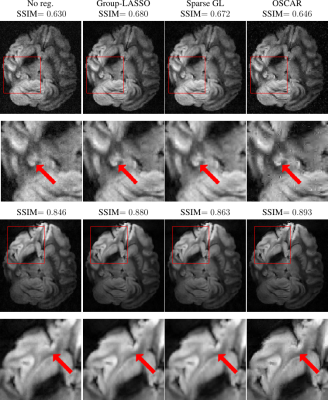
Results. Fig.2 compares the results of the SOS for the different penalizations, in terms of SSIM and image quality. It suggests that the group structure is more important than the intra group sparsity since OSCAR performs better.

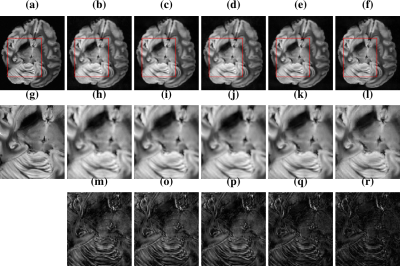
Fig.3 shows the coil-by-coil images, the structure is better preserved by the OSCAR regularization at the expense of low SNR value as seen on Fig.4 (first row).

Conclusion

Acknowledgements

This research program was supported by a 2016 DRF Impulsion grant (COSMIC, P.I.: P.C.)

References

1. A. Majumdar and R. Ward, “Calibration-less multi-coil MR image reconstruction,” Magnetic Resonance in Medicine, vol. 30, no. 7, pp. 1032–1045, 2012.

2. I. Chun, B. Adcock, and T. Talavage, “Efficient compressed sensing SENSE pMRI reconstruction with joint sparsity promotion,” IEEE transactions on Medical Imaging, vol. 35, no.1, pp. 354–368, 2016.

3. J. Friedman, T. Hastie, and R. Tibshirani, “A note on the group lasso and a sparse group-lasso,” arXiv preprint arXiv:1001.0736, 2010.

4. H. Bondell and B. Reich, “Simultaneous regression shrinkage, variable selection, and su-pervised clustering of predictors with OSCAR,” Biometrics, vol. 64, no. 1, pp. 115–123,2008.

5. Z. X. and M. Figueiredo, “The ordered weighted l1 norm: Atomic formulation, projections,and algorithms,” arXiv preprint arXiv:1409.4271, 2014.

6. M. Uecker, P. Lai, P., M.J. Murphy, P. Virtue, M. Elad, J.M. Pauly, and M. Lustig "ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA," Magnetic resonance in medicine, 71(3), 990-1001.

7. N. Pustelnik, A. Benazza-Benhayia, Y. Zheng, and J.-C. Pesquet, Wavelet-Based ImageDeconvolution and Reconstruction, pp. 1–34, American Cancer Society, 2016.

8. L. Condat, “A primal–dual splitting method for convex optimization involving lipschitzian,proximable and linear composite terms,” Journal of Optimization Theory and Applications,vol. 158, no. 2, pp. 460–479, Aug 2013.

9. B. Vũ, “A splitting algorithm for dual monotone inclusions involving cocoercive operators,”Advances in Computational Mathematics, vol. 38, no. 3, pp. 667–681, Apr 2013.

10. P. L. Combettes and J.-C. Pesquet, “Proximal splitting methods in signal proces- sing”, in Fixed-Point Algorithms for Inverse Problems in Science and Engineering, H. H. Bau- schke, R. Burachik, P. L. Combettes, V. Elser, D. R. Luke, and H. Wolkowicz editors. Springer- Verlag, New York, pp. 185-212, 2011

11. C. Lazarus, P. Weiss, N. Chauffert, F. Mauconduit, L. El Gueddari, C. Destrieux, I. Zemmoura, A. Vignaud, and P. Ciuciu, “Variable density k-space filling curves for accelerated Magnetic Resonance Imaging,” 2018.