4515
Retrospective 3D spiral trajectory correction: Exponential decay model vs. GIRF1Core-Facility Small Animal Imaging (CF-SANI), Ulm University, Ulm, Germany, 2Ulm University, Ulm, Germany, 3Ulm University Medical Center, Ulm, Germany, 4Experimental Cardiovascular MRI (ExCaVI), Ulm University Medical Center, Ulm, Germany
Synopsis
Uncorrected gradient imperfections lead to degrading image artifacts, especially in the case of demanding 3D trajectories. Different post-processing methods have been introduced to compensate for the real-time behaviour of the gradient system. This work shows that gradient waveform deviations can be vastly and nearly equally corrected using an exponential decay model as well as the gradient impulse response function. Both approaches were applied to a pure 3D spiral-like trajectory (Seiffert's spiral), achieving a comparable enhancement in image quality.
Introduction
Eddy currents in the gradient system1 and mechanical oscillations lead to frequency dependent deviations between the input and output of the gradient system. Such gradient imperfections result in changes in the measured $$$k$$$-space trajectory when being disregarded, giving rise to image blur, distortions2 or ghosting3. Especially trajectories which use high and non-constant gradient amplitudes and slew-rates are prone to gradient deviations for which the MRI system's intrinsic multi-exponential correction terms (pre-emphasis) are not sufficient.
A straightforward correction of remaining Eddy current effects can be retrospectively achieved by using an exponential model4 which is based on the decaying time course of induced currents. In addition, a more accurate compensation and characterization of the specific gradient system can be obtained by measuring the gradient impulse response function (GIRF)3,5. Since the latter is measured for each spatial gradient component, including delays of the gradient system, a improved enhancement in image quality is usually expected.
Methods
All data was acquired using a 3T wholebdy MRI system (Achieva 3T, Philips, Best, The Netherlands) with a small volume T/R-coil for the GIRF measurements and a SENSE NV coil (Philips, Best, The Netherlands) for 3D Seiffert spiral in-vivo knee images. Seiffert spirals are based on Jacobian elliptic functions and lead to a low-discrepancy coverage of $$$k$$$-space by using a strictly reduced number of interleaves compared to the established 3D Cones approach6. The Jacobian elliptic functions lead to sinusoidal waveforms in each gradient channel and are therefore sensitive to gradient imperfections.
Gradient waveform deviations were compensated by a mono-exponential decay model. The actual gradient $$$g_\text{out}(t)$$$ is seen as a convolution of the theoretical gradient $$$g_\text{in}(t)$$$ with an exponentially decaying function:
$$\begin{equation} g_\text{out}(t) = g_\text{in}(t)*e^{-t/\tau}.\end{equation}$$
Best results were achieved using a time constant of $$$\tau=39$$$ $$$\mu$$$s.
The GIRF can be used under the assumption that the gradient system is a linear and time-invariant system. For the determination of the actual gradient waveform $$$Out(\omega)$$$, the Fourier transform of the theoretical gradient $$$In(\omega)$$$ was used and multiplied with the GIRF $$$H(\omega)$$$:
$$\begin{equation} Out(\omega)=In(\omega)\cdot H(\omega).\end{equation}$$
The Fourier transform of $$$Out(\omega)$$$ yields the actual gradient in the time-domain. The GIRF was determined using a small cylindrical phantom (inner diameter $$$d_i=4.2$$$ mm, outer diameter $$$D_o=5.0$$$ mm and length $$$l=18$$$ mm) which was filled with water and contrast agent. The phantom was displaced from the isocenter and excited non-selectively. The signal was acquired during a chirp gradient5 and the GIRF in $$$x$$$-, $$$y$$$- and $$$z$$$-direction was determined.
Results and Discussion
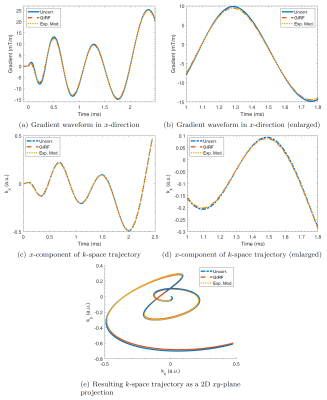
Figure 1a,b) shows the gradient waveform for one interleave of the trajectory in $$$x$$$-direction. The corrected gradient waveforms using both approaches are nearly identical, with arising deviations from the uncorrected waveform especially in regions where the slew-rate changes its sign. This behaviour is identical for all gradient channels. Since the corrected trajectory is obtained by integration of the gradient waveforms, small deviations between both correction approaches sum up as the read-out duration increases. Therefore, the shapes of the corrected $$$k$$$-space interleave differ only noticeable for high $$$k$$$-space values as can be appreciated in figure 1c,d,e).
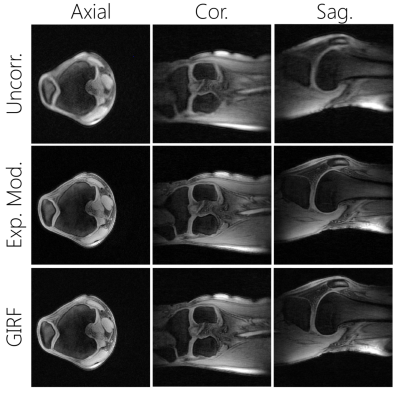
Knee images were successfully corrected using the GIRF and the exponential decay model (see figure 2). Compared to the uncorrected images, both approaches lead to considerably reduced blur and structures like tendons or ligaments become clearly visible.
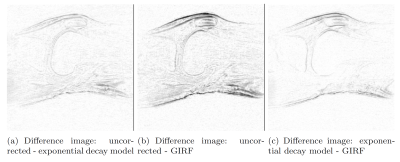
Difference images were calculated for better comparison of the uncorrected and the corrected images (see figure 3). The GIRF approach shows an enhanced correction at tissue interfaces and edges compared to the exponential model which is in accordance to the obtained $$$k$$$-space interleave deviations.
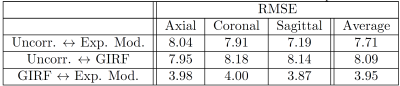
The difference images were compared quantitatively using the RMSE with values shown in figure 4. By averaging over all three anatomical planes, the RMSE confirms the higher impact of the GIRF approach on the uncorrected image. Nevertheless, the difference in RMSE between the GIRF and exponential model are small considering the RMSE values with respect to the uncorrected images. This supports the optical impression, that a qualitative enhancement in image quality can already be obtained by application of the exponential decay model.
Conclusion
The GIRF and the exponential decay model are two well suited approaches for the correction of gradient imperfections during image reconstruction. Both methods lead to a strict reduction of image blur, yielding highly improved image qualities. However, the GIRF is better suited for the correction of higher $$$k$$$-space values, but the impact of these deviations appear to be small. Eventually, for the 3T Achieva MR system, a need for GIRF measurements or for additional multi-exponential decay models cannot be concluded according to the shown evaluation.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No. 667192.
The authors thank the Ulm University Centre for Translational Imaging MoMAN for its support.
References
[1] Ch. Boesch, R. Gruetter and E. Martin. Temporal and spatial analysis of fields generated by eddy currents in superconducting magnets: optimization of corrections and quantitative characterization of magnet/gradient systems. Magnetic resonance in medicine 20, 268-284, 1991.
[2] H. Tan and C. Meyer. Estimation of k-space trajectories in spiral MRI. Magnetic resonance in medicine 61, 1396-1404, 2009.
[3] N. Addy, H. Wu and D. Nishimura. Simple method for MR gradient system characterization and k-space trajectory estimation. Magnetic resonance in medicine 68, 120-129, 2012.
[4] M. Alley, G. Glover and N. Pelc. Gradient characterization using a Fourier-transform technique. Magnetic resonance in medicine 39, 581-587, 1998.
[5] H. Liu and G. Matson. Accurate measurement of magnetic resonance imaging gradient characteristics. NIH-PA Author Manuscript 7, 1-15, 2013.
[6] P. T. Gurney, B. A. Hargreaves and D. G. Nishimura. Design and analysis of a practical 3D cones trajectory. Magn Reson Med. 55, 575-582, 2006.
Figures