4447
Deep learning motion compensation for Cartesian and spiral trajectories1Biomedical Engineering, University of Virginia, Charlottesville, VA, United States, 2Electrical and Computer Engineering, University of Virginia, Charlottesville, VA, United States
Synopsis
Movement of the subject during MRI acquisition causes image quality degradation. In this study we adopted a deep CNN to correct motion-corrupted brain images. To get paired training datasets, synthetic motion artifacts were added by simulating k-space data along different sampling trajectories. Quantitative evaluation showed that the CNN significantly improved the image quality. The spiral trajectory performed better than the Cartesian trajectory both before and after the motion deblurring. A network trained with an L1 loss function achieved better RMSE and SSIM than one trained with an L2 loss function after convergence. Overall, deep learning yields rapid and flexible motion compensation.
Introduction
During MRI acquisition, subject motion can severely degrade the resulting images by introducing ghosting and blurring. Spiral sampling is motion insensitive compared with Cartesian sampling because of its high data acquisition efficiency and oversampling of the k-space center. Since deep convolutional neural networks (CNNs) have shown great success in natural image denoising1, we aim to adopt a deep learning method to perform motion compensation in the image domain and compare the performance of the method using Cartesian and spiral trajectories.Methods
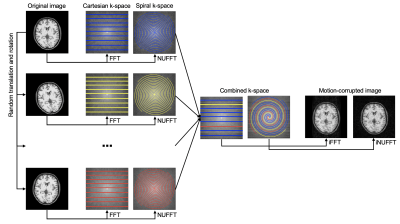
Brain images were obtained from an open database2, which comprises T1 weighted FLASH magnitude images for 88 subjects, acquired at 1$$$\times$$$1$$$\times$$$1 mm3. Each subject’s image contains 160 or 176 axial slices. 4362 slices were randomly selected as the training data, and the remaining 1364 slices were selected as the test data. Preprocessing included padding each image to 256$$$\times$$$256 and intensity normalization. To simulate motion artifacts, both the original images and translated and rotated images were first transformed into Cartesian k-space by a fast Fourier transform (FFT) or into spiral k-space by a nonuniform FFT (NUFFT)3. Then specific phase-encoding lines or spiral interleaves in the original k-space were replaced with the corresponding lines or interleaves from the transformed images. The final motion-corrupted images were reconstructed from the “combined” k-space by inverse FFT or inverse NUFFT4, as shown in Figure 1. The same percentage of phase-encoding lines or spiral interleaves were corrupted to ensure that the motion artifacts were comparable for different trajectories.
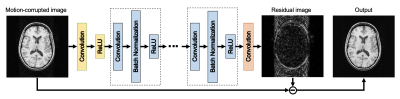
Figure 2 shows the network architecture. The deep CNN was implemented using TensorFlow, based on a model first proposed for natural image denoising1. The input of the network is the magnitude-only motion-corrupted image. After several convolution layers with batch normalization and ReLU, a residual image is predicted and the output of the network is produced by subtracting the residual image from the input. We trained the network for Cartesian and spiral trajectories separately. The parameters were optimized using the Adam5 optimizer with L1 loss function $$$L=|I_{target}-I_{output}|$$$ and learning rate 0.001. We also implement the L2 loss function $$$L=(I_{target}-I_{output})^2$$$ with learning rate 0.0001 to compare the performance.
Results
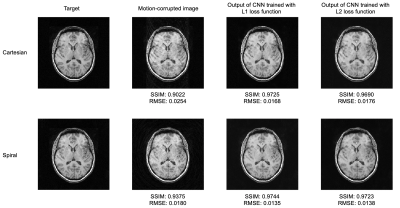
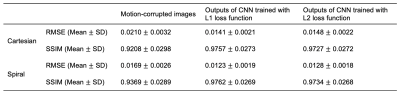
A representative example of motion-corrupted image and network output are shown in Figure 3. As the root mean squared error (RMSE) of output images decreased and the structural similarity index (SSIM) increased, the network successfully improved the image quality for both Cartesian and spiral sampling patterns. Table 1 provides the evaluating results of network performance on the whole test dataset. As spiral k-space sampling has the advantage of motion insensitivity, the quality of motion-corrupted images with spiral trajectory was higher than that with Cartesian trajectory. After motion compensation, the performance of the network with the spiral trajectory was still better than with the Cartesian trajectory. The CNN trained with L1 loss function reached lower RMSE than that trained with L2 loss function, which suggests that L2 loss may suffer more from local minimums6. In a few cases, the outputs of network were degraded compared with the inputs.Discussion
By training on brain images with simulated motion, an image domain motion correction CNN was developed. This work demonstrates that a deep learning-based method is capable of removing motion artifacts for both spiral and Cartesian MR images. Spiral outperforms Cartesian in motion robustness both before and after motion correction. Training the network with non-rigid motion data and testing it on real motion data will be performed to check the model’s performance and robustness. In addition, phase information will be incorporated into the network and the influence of different spiral trajectory designs will be explored.Acknowledgements
NIH R21EB022309, Siemens Medical SolutionsReferences
- Zhang K, Zuo W, Chen Y, Meng D, Zhang L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Transactions on Image Processing. 2017 Jul;26(7):3142-55.
- Bullitt E, Zeng D, Gerig G, Aylward S, Joshi S, Smith JK, Lin W, Ewend MG. Vessel tortuosity and brain tumor malignancy: a blinded study. Academic radiology. 2005 Oct 1;12(10):1232-40.
- Fessler JA. Michigan Image Reconstruction Toolbox. Available at https://web.eecs.umich.edu/~fessler/code/
- Lorch B, Vaillant G, Baumgartner C, Bai W, Rueckert D, Maier A. Automated Detection of Motion Artefacts in MR Imaging Using Decision Forests. Journal of medical engineering. 2017;2017.
- Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. 2014 Dec 22.
- Zhao H, Gallo O, Frosio I, Kautz J. Loss functions for image restoration with neural networks. IEEE Transactions on Computational Imaging. 2017 Mar;3(1):47-57.