3534

Comparison and Assessment of IVIM-MRI Methods Using a Capillary Flow Phantom

Moritz Jörg Schneider^1,2, Thomas Gaass^1,2, Julien Dinkel^1,2, Jens Ricke¹, and Olaf Dietrich¹

¹Department of Radiology, LMU University of Munich, Munich, Germany, ²Comprehensive Pneumology Center, German Center for Lung Research, Munich, Germany

Synopsis

In this study different intravoxel incoherent motion (IVIM) MRI methods were assessed and compared using phantom measurement. The phantom was constructed to mimic a capillary bed and allowed for the controlled application of fluid flow at varying rates. Advanced IVIM MRI methods beyond the biexponential pseudo-diffusion model were shown to be capable of accurately characterizing fluid flow inside a capillary network yielding intuitive parameters in a reproducible manner.

Introduction

Intravoxel incoherent motion imaging (IVIM)¹ allows to assess capillary perfusion non-invasively using diffusion-weighted MRI. IVIM-MRI data is commonly analyzed using the biexponential pseudo-diffusion model² yielding the tissue diffusivity $$$D$$$, the fraction $$$f$$$ of signal attributed to blood in perfused capillaries and the pseudo-diffusion coefficient $$$D^\ast$$$. Recently, a "phase-distribution" approach based on the simulation of particle pathways while considering a distribution of particle speeds was presented³. In place of $$$D^\ast$$$, this method yields the (average) particle flow speed $$$v$$$, the time $$$t$$$ until a particle changes its movement direction and also the length of a capillary segment via $$$l=vt$$$. However, the in-vivo validation of IVIM-MRI methods is inherently difficult. Measures such as the blood flow velocity and the capillary length are challenging to determine in vivo and they cannot easily be regulated. Therefore, the purpose of this study is the systematic analysis of IVIM MRI methods using a perfusable capillary phantom.

Methods

As previously described^4,5, a perfusable capillary phantom designed to mimic fluid flow inside a interconnected network of randomly oriented channels was constructed using sacrificial sugar fibers embedded in synthetic resin. The capillary network was characterized using optical microscopy. The phantom allowed for the application of controlled fluid flow at variable rates while performing IVIM-MRI experiments on a 3 T whole-body MRI system (Skyra, Siemens Healthcare, Erlangen, Germany). For each flow rate (ranging from 0.2 ml/min to 2.4 ml/min), data was acquired using four different single shot EPI DW-MRI sequences (two with monopolar diffusion gradient schemes and two with flow-compensated schemes of varying diffusion preparation duration) with up to 16 b-values between 0 and 800s/mm². Signal intensities were averaged over a region of interest covering the capillary network and subsequently analyzed using the phase-distribution model as well as the biexponential pseudo-diffusion model (only the data from one sequence with monopolar gradients was used for the biexponential model). For the biexponential model, $$$v$$$ was calculated via⁶ $$$v=6D^\ast/l$$$. The phase-distribution model accounted for a continuous particle speed distribution (derived from a Pareto distribution) based on findings⁷ about fluid flow in fracture networks. A second measurement series was performed on a different day to assess the reproducibility.

Results

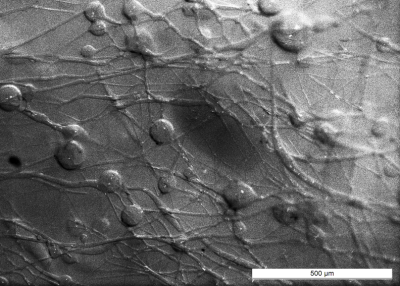
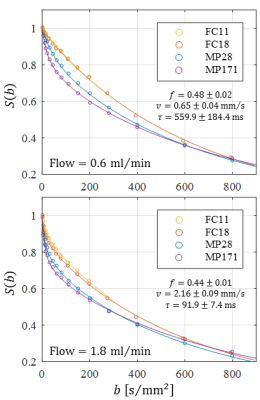
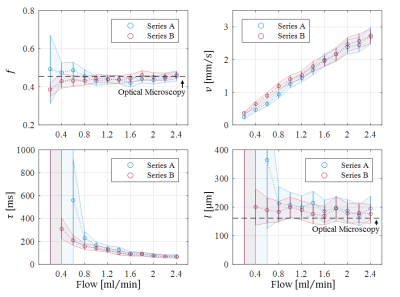
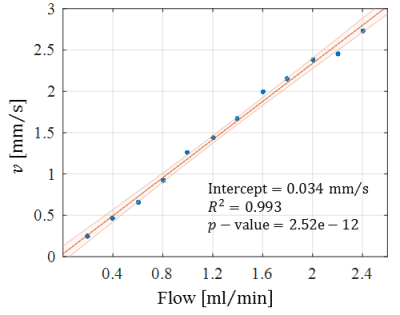
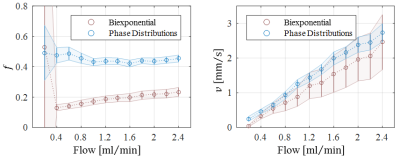
Optical microscopy revealed a dense and highly interconnected network of randomly oriented capillaries strewn with spherical dilations (Figure 1). Optical microscopy yielded the average capillary length of 162±78µm, the average capillary diameter of 11.4±4.4µm and the ratio of the volume inside the capillaries to the total (capillaries plus dilations) network volume of 0.454±0.002. The acquired data was best described by a two-compartment model consisting of a static and a flowing compartment. Exemplary fits of the phase-distribution model are illustrated in Figure 2. Figure 3 displays the estimated parameters using the phase-distribution model for both measurement series. A regression analysis of the particle speed $$$v$$$ versus the applied flow is displayed in Figure 4. Figure 5 compares the signal fraction $$$f$$$ and $$$v$$$ estimated using the phase-distribution model versus the biexponential model.

Discussion

The phase-distribution model allowed for an excellent fit to the acquired data at all flow rates and yielded reasonable parameter estimates with little variation in between measurement series. The estimated signal fraction $$$f$$$ attributed to the flowing compartment stayed approximately constant over the applied flow rates and agreed well with the ratio of the volume inside the capillaries to the total (capillaries plus dilations) network volume estimated via optical microscopy. Thus, the static compartment is hypothesized to be ascribed to non-flowing liquid inside the spherical dilations. Judging from the highly significant linear proportionality, practically all variation in $$$v$$$ is predictable from the applied flow rate. At very slow flow rates, the characteristic duration $$$t$$$ until a directional change occurs could not be determined with satisfactory accuracy. At flow rates greater than 0.8ml/min, $$$t$$$ showed an inverse proportionality to the applied flow rate. Consequently, the estimated capillary segment length of about 195μm stayed approximately constant in this domain and agreed well with the value determined via optical microscopy. Using the biexponential model, the signal fraction $$$f$$$ was heavily underestimated and displayed a strong dependence on the applied flow rate. Yet, the estimated particle speed closely followed the particle speed determined using the phase-distribution model.

Clonclusion

The constructed phantom facilitated the detailed investigation of IVIM-MRI methods. The results demonstrate that the advanced phase-distribution method is capable of accurately characterizing fluid flow inside a capillary network. Parameters estimated using the conventional biexponential model, specifically the perfusion fraction $$$f$$$, were shown to be subject to a potential bias if the model assumptions are not met by the underlying flow pattern.

Acknowledgements

No acknowledgement found.

References

1. Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology. 1986;161(2):401-407. doi:10.1148/radiology.161.2.3763909

2. Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988;168(2):497-505. doi:10.1148/radiology.168.2.3393671

3. Wetscherek, A., Stieltjes, B. & Laun, F. B. Flow-compensated intravoxel incoherent motion diffusion imaging. Magn. Reson. Med. 74, 410–419 (2015).

4. Bellan LM, Singh SP, Henderson PW, Porri TJ, Craighead HG, Spector JA. Fabrication of an artificial 3-dimensional vascular network using sacrificial sugar structures. Soft Matter. 2009;5(7):1354. doi:10.1039/b819905a

5. Gaass T, Schneider MJ, Dietrich O, Ingrisch M, Dinkel J. Technical Note: Quantitative dynamic contrast-enhanced MRI of a 3-dimensional artificial capillary network. Med Phys. 2017;44(4):1462-1469. doi:10.1002/mp.12162

6. Bihan DL, Turner R. The capillary network: a link between ivim and classical perfusion. Magn Reson Med. 1992;27(1):171-178. doi:10.1002/mrm.1910270116

7. Frampton A, Cvetkovic V. Upscaling particle transport in discrete fracture networks: 1. Nonreactive tracers. Water Resour Res. 2007;43(10):W10428. doi:10.1029/2006WR005334

Figures

Figure 1: Exemplary microscopy image of the capillary network taken with a DM2500 (Leica, Wetzlar, Germany) optical microscope. A highly interconnected capillary system is left by the dissolved sugar structures, strewn with spherically shaped dilations presumably caused by residual air bubbles and sugar crystals.

Figure 2: Measured signal intensities (different sequences color coded) at exemplary flow rates of 0.6ml/min and 1.8ml/min and the respective fits using the phase-distribution model. In general, the signal model fits the measured data well as the fitted curves closely follow the measurement points. At all applied flow rates, the signal decay is slowed using the flow-compensated sequences FC11and FC18 indicating that the pseudo-diffusion limit is not reached.

Figure 3: Estimated parameters and respective 95% confidence intervals. For flow rates above 0.8ml/min the confidence intervals are appreciably small, with $$$f$$$ remaining largely constant and $$$t$$$ showing an inverse proportionality to the applied flow rate. The estimated average particle speed $$$v$$$ shows a linear proportionality to the applied rate of flow with narrow confidence intervals. The average capillary segment length calculated via $$$l=vt$$$ remains approximately constant at flow rates above 0.8ml/min and is close to the average segment length of 162μm determined using optical microscopy (dashed line).

Figure 4: Regression analysis of $$$v$$$ (measurement series A) versus the applied flow yields a highly significant linear proportionality. The estimated intercept at 0.034mm/s indicates that there is little systematic bias.

Figure 5: Comparison of the signal fractions $$$f$$$ and the particle speeds $$$v$$$ estimated using the phase-distribution and biexponential model. For the biexponential model, the particle speed was calculated via $$$v=6D^\ast/l$$$, whereby a capillary length of $$$l$$$=195μm (average of $$$l$$$ estimated using phase-distribution model) was used. The biexponential estimate for $$$f$$$ is much lower than the estimate obtained using the phase-distribution model, however, the estimates for $$$v$$$ show a reasonable agreement between the two models.

Proc. Intl. Soc. Mag. Reson. Med. 27 (2019)

3534