3491
An accurate surface-to-volume ratio estimation by general diffusion gradient waveform1Laboratoire PMC, Ecole Polytechnique, Palaiseau, France, 2NORMENT, KG Jebsen Centre for Psychosis Research, Oslo University Hospital, Oslo, Norway, 3Institute of Clinical Medicine, University of Oslo, Oslo, Norway
Synopsis
We generalize Mitra’s formula for estimating the surface-to-volume ratio of an anisotropic medium with any pore shapes by using arbitrary diffusion gradient waveforms. We show that the surface-to-volume ratio can be significantly misestimated using the original formula without taking into account the applied diffusion gradient profile. For an accurate estimation, we derive new “isotropy” criteria which ensure that the diffusion weighted sequence is insensitive to the mesoscopic anisotropy of the sample. As a result, we introduce a novel class of porous media characteristics which are useful for biomedical applications.
Introduction
Mitra et al.1 discovered an excellent opportunity of diffusion MRI to probe the surface-to-volume ratio as a quantitative descriptor of microstructures in different porous media, for example, in biological tissues such as brain and lungs. However, their work was focused on pulsed-gradient echo (PGSE) sequences with very short gradient pulses, which require high gradients and are not easy to achieve in clinical scanners. Moreover, Mitra’s formula was provided only for simple pore shapes often exploited in modeling: slabs, cylinders, and spheres. Here, we present a generalization of Mitra’s formula for arbitrary gradient profile and any pore shape. We apply our results to 3D gradient waveforms, e.g. isotropic diffusion weighting2.Results
We consider a gradient profile $$${\boldsymbol{g}}(t)$$$ starting at $$$t=0$$$, ending at the echo time $$$t=T$$$, and obeying the refocusing condition $$$\boldsymbol{q}(T)=\boldsymbol{0}$$$, where $$$\boldsymbol{q}(t)=\int_0^t \boldsymbol{g}(t')\,\mathrm{d}t'$$$. Using mathematical techniques detailed in Ref3, we derived the short-time asymptotic behavior of the effective (or apparent)
diffusion coefficient probed by diffusion MRI4:
$$D(T)=D\left(1-\eta\frac{4}{3\sqrt{\pi}}\frac{S}{V}\sqrt{DT}+O(T)\right)\;,\label{eq:D}$$
where $$$D$$$ is the intrinsic diffusion coefficient, $$$S/V$$$ is the surface-to-volume ratio of the medium and $$$O(T)$$$ means that the next term is at most of order of $$$T$$$. The dimensionless prefactor $$$\eta$$$ couples the underlying structure of the medium and the gradient waveform:
$$\eta=\frac{\mathrm{Tr}\left(\mathcal{W}\mathcal{F}^{(3)}\right)}{b\sqrt{T}}\;,$$
where $$$\mathrm{Tr}$$$ is the trace. Here we introduced the ``temporal'' matrix $$$\mathcal{F}^{(3)}$$$,
$$\mathcal{F}^{(m)}=-\frac{\gamma^2}{2}\int_0^T\int_0^T \boldsymbol{g}(t_1)\otimes\boldsymbol{g}(t_2) \lvert t_2 - t_1 \rvert^{m/2}\,\mathrm{d}t_1\,\mathrm{d}t_2\;,$$
(with $$$m=3$$$), and the ``structural'' matrix
$$\mathcal{W}=\frac{1}{S}\int_{\partial\Omega} \boldsymbol{n}\otimes\boldsymbol{n}\,\mathrm{d}S\;,$$
where the integration is performed on the boundary $$$\partial \Omega$$$ of the domain $$$\Omega$$$ and $$$\boldsymbol{n}$$$ is the unit outward normal vector to the boundary.
We used the tensor product notation $$$\otimes$$$: if $$$\boldsymbol{a}$$$ and $$$\boldsymbol{b}$$$ are vectors, then $$$\boldsymbol{a}\otimes\boldsymbol{b}$$$ is a matrix with components $$$\left(\boldsymbol{a}\otimes\boldsymbol{b}\right)_{ij}=a_ib_j$$$. The next order terms involve the matrices $$$\mathcal{F}^{(4)}, \mathcal{F}^{(5)}, \ldots$$$ coupled with structural matrices that characterize the medium structure and properties such as curvature or permeability.
Discussion
An accurate estimation of $$$S/V$$$ from the measured $$$D(T)$$$ requires a precise computation of the factor $$$\eta$$$, which couples the gradient profile to the structure of the medium.
Linear Gradient Encoding
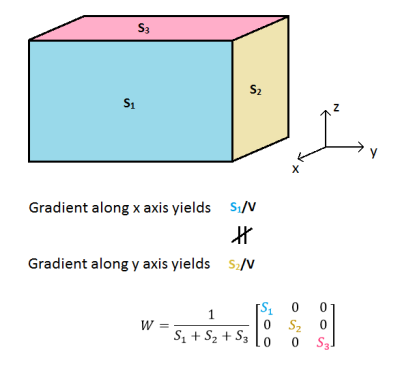
In the case of linear gradient encoding when $$$\boldsymbol{g}(t)$$$ has a fixed direction, $$$\eta$$$ may depend on the gradient direction
if the medium is anisotropic (an example is shown on Figure 1). Conversely,
this property may be used to obtain partial information about the pore structure. For
instance, a medium modeled by a bundle of cylindrical fibers yields a
voxel-averaged $$$\mathcal{W}$$$-matrix which contains information about the orientation
dispersion of the fibers.
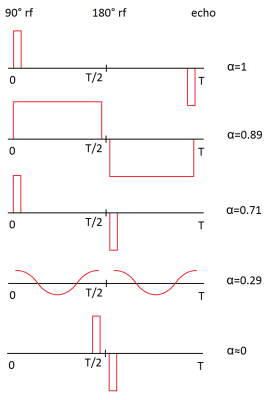
Even if the medium is isotropic (e.g., a spherical pore), $$$\eta$$$ strongly depends on the gradient waveform. For example, one can achieve arbitrary small values of $$$\eta$$$ with fast oscillating gradients, whereas Mitra’s formula corresponds to $$$\eta_{\mathrm{Mitra}}=1/d=1/3$$$ (d=dimensionality). Figure 2 illustrates different gradient profiles with the corresponding value of $$$\alpha=\eta/\eta_{\mathrm{Mitra}}=3\eta$$$. Applying the classical Mitra formula without taking $$$\eta$$$ into account may lead to significant underestimation of surface-to-volume ratios, and thus, overestimation of the typical size of compartments.
3D Gradient Sequence
The case of 3D gradients is richer and allows one to
design sequences that are insensitive to the mesoscopic anisotropy of the
confining pores. This makes the determination of $$$S/V$$$ independent of
the orientation of the medium, and thus more precise. This is performed by
imposing that the $$$\mathcal{F}^{(3)}$$$ matrix is invariant under any spatial rotation, that
is, proportional to the $$$3\times 3$$$ unit matrix $$$I$$$: $$$\mathcal{F}^{(3)}\propto I$$$. This condition ensures that the prefactor $$$\eta$$$ does not depend on the structural matrix $$$\mathcal{W}$$$ and thus on the mesoscopic anisotropy. Interestingly, this condition is not the one realized
by usual spherical encoding sequences2, $$$\mathcal{F}^{(2)}\propto I$$$. This finding leads to the design of diffusion
sequences that are more robust to anisotropic media.
Conclusion
The present generalization of Mitra’s formula has a great practical impact for clinical applications. General diffusion gradient profiles implemented with experimental limitations may help to introduce a novel class of biomarkers based on accurate surface-to-volume ratio, structural parameterization by $$$\mathcal{W}$$$ matrix and option for designing of “temporal” matrices $$$\mathcal{F}^{(m)}$$$ with desired properties. Thus, the proposed approach can be applied for investigating mesoscopic anisotropy of different character such as grey and white matter in the human brain.Acknowledgements
No acknowledgement found.References
[1] P. P. Mitra, P. N. Sen, L.
M. Schwartz, and P. Le Doussal, Phys.
Rev. Lett. 68 3555-3558 (1992)
[2] S. Eriksson, S. Lasič, and D. Topgaard, J.
Magn. Res. 226 13-18 (2013)
[3] D. S. Grebenkov, Rev. Mod. Phys. 79 1077-1137 (2007)
[4] N. Moutal, I. I. Maximov, and D. S. Grebenkov,
ArXiv:1811.01568
Figures