3346
Multi-shot Diffusion EPI Reconstruction with Iterative Rigid Motion-correction and Motion-induced Phase-correction for Brain Imaging1Institute for Signal Processing, University of Lübeck, Lübeck, Germany, 2Philips Research Hamburg, Hamburg, Germany, 3Dept. Radiology, LUMC, Leiden, Netherlands
Synopsis
Multi-shot diffusion-weighted imaging offers increased SNR and higher resolution, but makes the acquisition vulnerable to shot-specific phase variations and macroscopic inter-shot motion. A wide range of iterative phase-corrected reconstruction schemes have been proposed to overcome the inter-shot phase inconsistencies, but robust motion estimation is still challenging due to the inherently low SNR of DWI. This work moves forward from initial one-time rigid motion estimation to an alternating optimization balancing the joint image, phase and motion estimation. A novel multi-shot echo-planar diffusion algorithm with iterative motion and phase correction is presented in simulations and in-vivo.
Introduction
Multi-shot techniques are widely studied for diffusion applications to increase imaging resolution compared to single-shot echo-planar imaging (EPI) as the current clinical standard1. However, segmented acquisitions require more sophisticated reconstruction algorithms due to both motion-induced phase variations2 and macroscopic motion. For phase-corrected reconstructions, several SENSE-based3 algorithms exist estimating the phase variations once like SENSE+CG4 or iteratively like POCS-ICE5 and POCSMUSE6. The AMUSE algorithm7 also integrates an initial one-time rigid motion correction into the multi-shot diffusion reconstruction which might fail from the low SNR in the data. In this abstract, an iterative phase and motion correction (MC) algorithm is presented and evaluated to address this problem.Methods
Multi-shot reconstruction mutually relates the shot images $$$x_i$$$ by a consensus constraint $$$x_i=\Phi_i\Omega_i x$$$, which, in case of DWI, contains a shot-specific motion operator $$$\Omega_i$$$ and phase operator $$$\Phi_i$$$. $$$x$$$ is the joint image and $$$i$$$ the shot index. The joint functional is then given as the sum of the shot data consistencies with the data $$$d$$$, the undersampled Fourier operator $$$F$$$ and the SENSE operator $$$S$$$.
$$\underset{x, \Phi_i, \Omega_i}{arg min} \sum_i \lVert F_i S \Phi_i \Omega_i x - d_i \rVert_2^2$$
Three algorithm variants were implemented alternately optimizing the phase, motion, and image estimation. The basic scheme is visualized in Figure 1. As motion correction (MC) is generally a non-convex optimization, all algorithms start with an initial CG-SENSE8 shot guess. Then, shot registration and alignment are performed, whereby the shot with the highest correlation to all other shots is chosen as reference. Next, an optional data rejection module follows to account for through-plane motion. Phase estimation is subsequently performed by a 2D triangular k-space window4 scaled to half the image size. From this point:
1) MC-SENSE+CG performs a final conjugate gradients (CG) algorithm extending conventional SENSE+CG3 by the estimated motion operator within the forward model.
2) Iterative-MC scheme reapplies the shot-wise phase and motion operators and performs a gradient-based SENSE update to recover the next shot guesses. Then, the algorithm iteratively repeats this process until convergence.
3) Prior-MC scheme adapts the iterative procedure of Iterative-MC, but skips the motion estimation relying on the initial motion estimate.
Motion estimation was achieved by a rigid preregistration based on the fast elastic image registration9 using a normalized gradient field metric. Motion transformations were performed by k-space operations10. Gradient operations were performed by image space operations regular Cartesian undersampling properties. Data rejection was tested by shot correlation threshold after alignment. Coil compression was performed by PCA with 99%-threshold.
The algorithms were evaluated in BrainWeb11 simulations and in-vivo. For simulations, 12 2D-Gaussian sensitivities were arranged circularly around the head. Phase maps were created12, rigid motion was sampled uniformly from a range of $$$\pm 5 \, pix$$$ and $$$\pm 10°$$$, $$$N_{shots}=\{2, 3, 4, 5, 6\}$$$ and $$$SNR=\{10, 20, 30, 40\}$$$. Performance was averaged over 10 random cases. For in-vivo evaluation, multi-shot EPI DWI brain data was attained from 5 healthy volunteers using a 13-channel head coil, 3T Philips Ingenia, $$$b=\{0, 1000\} \, \dfrac{s}{mm^2}$$$ with three orientations and $$$1 \times 1 \times 4 \, mm^3$$$ resolution. Informed consent was attained according to the rules of the institution.
Computations were performed using Python 3.6.5 on a 2.7GHz Intel Core i7 4-core CPU and 16 GB RAM. The algorithms were stopped when the residual error5 of subsequent iterations dropped below 10-3 or the iteration number exceeded 200. Phase estimation was disabled for $$$b=0 \, \dfrac{s}{mm^2}$$$ .
Results
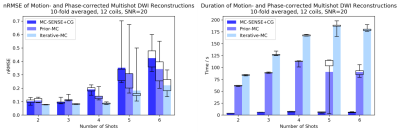
Normalized root-mean-square errors and durations of the simulations are shown in Figure 2 for varying segmentation. The time for iterative reconstruction increases tremendously with segmentation, but Iterative-MC has best performance.
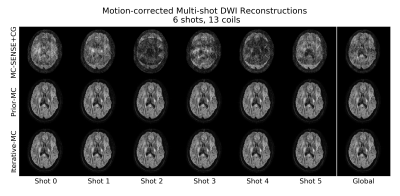
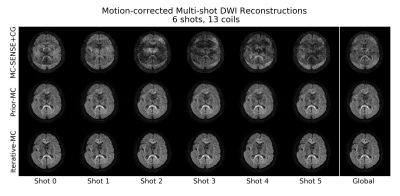
Figures 3 and 4 both show 6-shot in-vivo results with shot and global estimates. MC-SENSE+CG comprises strong motion and phase artifacts, whereas Prior-MC shows no visible artifacts in Figure 3 but blurring due to the heavy motion artifacts in Figure 4. Iterative-MC nicely recovers all cases.
Discussion
Iterative estimation of both phase and motion tremendously improves robustness in case of low SNR at the cost of increased computations, thereby making higher EPI segmentation feasible. Shot rejection based on shot correlation failed due to the strong intensity variations and noise (g-factor) in the shot guesses. At this point, we see this scheme is a valuable basis for deep learning modules to improve shot rejection, motion and phase estimation and thereby accelerate the iterative procedure.Conclusion
In conclusion, motion and phase correction were successfully combined within a novel algorithm for motion- and phase-corrected multi-shot EPI DWI. This scheme builds the basis for future modular extensions increasing the robustness against through-plane motion and further acceleration to ease clinical adoption of the method.Acknowledgements
No acknowledgement found.References
1. Wu W and Miller KL. Image formation in diffusion MRI: A review of recent technical developments: Review of Image Formation in dMRI. JMRI. 2017;46(3):646–662.
2. Miller KL and Pauly JM. Nonlinear Phase Correction for Navigated Diffusion Imaging. MRM. 2003;50:343-353.
3. Pruessmann et al. SENSE: sensitivity encoding for fast MRI. MRM. vol. 1999;42(5):952–962.
4. Truong TK, and Guidon A. High‐resolution multishot spiral diffusion tensor imaging with inherent correction of motion‐induced phase errors. MRM. 2014;71(2):790-796.
5. Guo et al. POCS‐enhanced inherent correction of motion‐induced phase errors (POCS‐ICE) for high‐resolution multishot diffusion MRI. MRM. 2016;75(1):169-180.
6. Chu et al. POCS-Based Reconstruction of Multiplexed Sensitivity Encoded MRI (POCSMUSE): A General Algorithm for Reducing Motion-Related Artifacts. MRM. 2015;74:1336–1348.
7. Guhaniyogi et al. Motion Immune Diffusion Imaging Using Augmented MUSE for High-Resolution Multi-Shot EPI. MRM. 2016;75:639-652.
8. Pruessmann et al. Advances in sensitivity encoding with arbitrary k‐space trajectories. MRM. 2001;46(4):638-651.
9. Kabus S and Lorenz C. Fast elastic image registration. Medical Image Analysis for the Clinic: A Grand Challenge. 2010:81-89.
10. Cordero-Grande et al. Sensitivity Encoding for Aligned Multishot Magnetic Resonance Reconstruction. IEEE Transactions on Computational Imaging. 2016;2(3):266-280.
11. Brainweb: Simulated Brain Database, http://www.bic.mni.mcgill.ca/brainweb/. Accessed July 27, 2017.
12. Hu et al. Phase-Updated Regularized SENSE for Navigator-Free Multishot Diffusion Imaging. MRM. 2017;78(1):172-181.
Figures