2443
A localized reconstruction method for parallel imaging in MRI1School of Electrical Engineering, Korea Advanced Institute of Science and Technology, Daejeon, Korea, Republic of, 2School of Medicine Stanford University, Palo Alto, CA, United States
Synopsis
Conventional parallel imaging methods reconstruct MR images from subsampled data, which utilizes spatial sensitivity information of multi-channel RF coil. In this study, localization of receiving coil sensitivity along readout direction (x) is introduced to efficiently utilize the coil sensitivity for parallel imaging. In the x-ky space, localization window is applied for estimation of missing data. Sensitivity localization in the readout direction makes near channels more weighted than distant channels for calculating estimation kernel. The proposed reconstruction method for parallel imaging considers the correlation between spatial sensitivities along the readout direction of receiving channels and region to be reconstructed.
INTRODUCTION
Parallel magnetic resonance(MR) imaging techniques have been developed to reduce the imaging time. Subsampled MR data is acquired and missing data lines are estimated from the acquired data using multi-channel radio frequency(RF) coil1. Each channel provides slightly different information and enables the missing data to be estimated. Conventional parallel reconstruction methods exploit whole subsampled data which contains entire spatial sensitivity information of multi-channel RF coil. Sensitivity difference between channels along phase encoding direction helps to estimate missing phase encoding lines1,2. However, data from spatially distant channel along the readout direction could disturb parallel reconstruction with noisy information. In this study, localization of receiving coil sensitivity along the readout direction is introduced to efficiently utilize the coil sensitivity for parallel imaging.METHODS
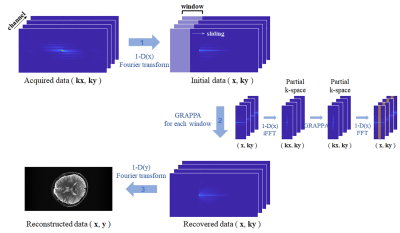
Since the sensitivity of the receiving coil is inversely proportional to the square of the spatial distance, the influence of the channel located spatially distant from the region to be estimates is low3. Therefore, the information from the channel located distant along the readout direction may not be helpful or may be a noise source for parallel imaging reconstruction. We propose a localized parallel reconstruction method. In order to localize the sensitivities of the receiving channels along the readout direction, firstly Fourier transform is performed in readout direction where the acquired data is not subsampled. Spatial sensitivity of the receiving channel is projected in the readout direction in $$$x-k_y$$$ space, where $$$x$$$ and $$$y$$$ mean the readout and phase encoding directions, respectively. In the $$$x-k_y$$$ space, localization window is applied for estimation of the missing data as shown in Figure 1. The window includes partial region in the readout direction($$$x$$$) and full in the phase encoding direction($$$k_y$$$). Inverse Fourier transform of the partial region is performed in the readout direction to partial $$$k_x-k_y$$$ space. Conventional GRAPPA reconstruction which is a parallel imaging technique in k-space domain4, is applied to the partial $$$k_x-k_y$$$ space. Through this process, data of distant channel whose position is far from the region to be estimated has small signal intensity and affects less for the estimation. The estimated partial $$$k_x-k_y$$$ space is transformed to the partial $$$x-k_y$$$ space and the central $$$k_y$$$ line of the partial $$$x-k_y$$$ space is used for image reconstruction. As the window slides along the readout direction in $$$x-k_y$$$ space, full data in $$$x-k_y$$$ space is obtained.RESULTS
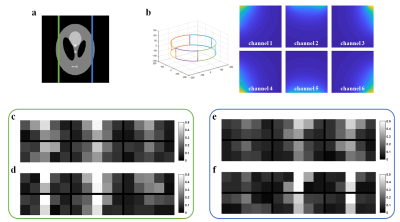
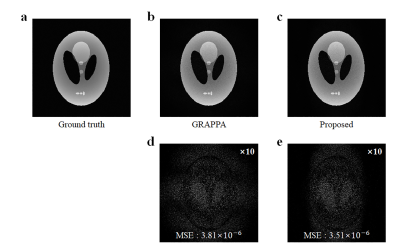
We conducted computer simulations to validate the proposed reconstruction method. Six-channel birdcage RF coil was designed5 and sensitivity of each channel was calculated using Biot-Savart’s law6 as shown in Figure 2. Modified Shepp-Logan phantom image with a matrix size of 256×256 was created and sensitivity of each channels was multiplied to the image. With a reduction factor of three, GRAPPA estimation kernel size of 2(PE)×5(RO), ACS lines of 24, conventional GRAPPA reconstruction and the proposed localized reconstruction were performed. In order to show the effect of sensitivity localization, GRAPPA estimation kernels were compared between the conventional GRAPPA and the proposed localized reconstruction. The conventional GRAPPA shares one estimation kernel for estimating all of the missing data. The proposed reconstruction has one estimation kernel for estimating data in each window. Figure 2 shows that kernel weights of the proposed method for higher sensitivity channels are greater than that of the conventional method. This means the influence of distant channels is small and the influence of near channels is large for the proposed method. The reconstructed images and differences from the reference image that was reconstructed from fully sampled data are shown in Figure 3. Noise from the proposed method is smaller and more restricted than that from the conventional reconstruction method.
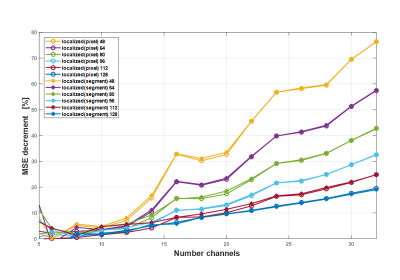
In order to show the effect of sensitivity localization, number of channels were changed and performance of the proposed reconstruction methods was analyzed. Number of channels increased only in the radial direction of the birdcage-shaped coil. As the channel sensitivities are localized, the performance of the proposed method increases as shown in Figure 4.
DISCUSSION
The proposed reconstruction method for parallel imaging considers the correlation between spatial sensitivities along the readout direction of receiving channels and region to be estimated. Sensitivity localization makes near channels more weighted than distant channels for calculating estimation kernel. This sensitivity localization enables more accurate estimation of missing phase lines. The performance of the proposed method depends on the degree of sensitivity localization. In general, sensitivities are more localized as number of channels increases. Other factors such as window size, number of readout points to be filled in estimation window could also affect performance and then would be further investigated.Acknowledgements
This research was supported by a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry for Health and Welfare, Korea (HI14C1135) and the Brain Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (2014M3C7033999).References
1. Deshmane, A., Gulani, V., Griswold, M. A., et al. Parallel MR imaging. Journal of Magnetic Resonance Imaging. 2012; 36(1): 55-72.
2. Griswold, M. A., Jakob, P. M., Nittka, M., et al. Partially parallel imaging with localized sensitivities (PILS). Magnetic Resonance in Medicine. 2000; 44(4): 602-609.
3. McVeigh, E. R., Bronskill, M. J., Henkelman, R. M.. Phase and sensitivity of receiver coils in magnetic resonance imaging. Medical physics. 1986; 13(6): 806-814.
4. Griswold, M. A., Jakob, P. M., Heidemann, R. M., et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2002; 47(6): 1202-1210.
5. Hayes, C. E., Edelstein, W. A., Schenck, J. F., et al. An efficient, highly homogeneous radiofrequency coil for whole-body NMR imaging at 1.5 T. Journal of Magnetic Resonance. 1969; 63(3): 622-628.
6. Giovannetti, G., Landini, L., Santarelli, M. F., et al. A fast and accurate simulator for the design of birdcage coils in MRI. Magnetic Resonance Materials in Physics, Biology and Medicine. 2002; 15(1-3): 36-44.
Figures