Synopsis

Under-sampled non-Cartesian trajectories play a vital role in accelerating MRI scan time; however, the solution image may have aliasing artifacts. In this work, a GROG gridding based Sparse-SENSE reconstruction is presented to get the solution image from the non-Cartesian under-sampled radial MR data. The proposed method is tested on 1.5T human head data at different acceleration factors (i.e. 4, 6 and 9) and compared with pseudo-Cartesian GRAPPA scheme. The results show that the proposed method provides significant improvement (e.g. 87% improvement in AP at AF=4) in the reconstructed images as compared to conventional pseudo-Cartesian GRAPPA reconstruction.

Introduction:

Method:

GROG ⁴ is a novel gridding technique that maps the acquired non-Cartesian data points to the nearest Cartesian locations in k-space. Moreover, GROG exploits self-calibrated coil-by-coil weight sets to grid the non-Cartesian data and leaves some empty positions in the gridded data. Pseudo-Cartesian GRAPPA with GROG has been proposed by Seiberlich et al. ³ for the reconstruction of MR images from under-sampled non-Cartesian data. It uses several patterns to estimate the coil-by-coil weight sets from auto-calibrated signal (ACS) lines and these estimated weights fill the missing positions of the GROG gridded k-space data to get the unaliased MR images. However, it is difficult to estimate the pseudo-Cartesian GRAPPA ³ weight estimating patterns in practice due to lack of symmetry in the GROG gridded k-space.

Compressed Sensing (CS) ⁶ is used for MR image reconstruction from a small subset of k-space samples. CS requires sparse representation of the acquired data in a transform domain, incoherent artifacts and a non-linear reconstruction method. Combining CS with pMRI utilizes multiple receiver coil sensitivity profiles that provide an additional image sparsity to get good quality MR images as compared to individual CS or pMRI techniques ⁵. In ⁵, a general method of Sparse-SENSE has been developed that combines compressed sensing and parallel imaging to reconstruct MR images from the pseudo-random Cartesian under-sampled data.

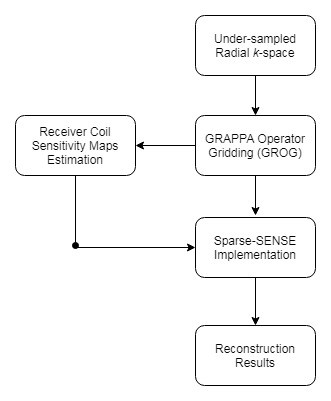
This work proposes a GROG based Sparse-SENSE method to reconstruct the artifact free MR images from radially encoded under-sampled MR data. The first step in the proposed method is to apply GROG on the acquired under-sampled radial data that provides an estimate of the Cartesian k-space. In the next stage, Eigenvalue based receiver coil sensitivity maps are estimated from center of GROG gridded data ⁷ that are incorporated with Sparse-SENSE reconstruction to get the artifact free solution image.

Figure 1 provides a block diagram of the proposed scheme. The performance of the proposed method and pseudo-Cartesian GRAPPA (conventional method) is evaluated using Artifact Power (AP), Root Mean Square Error (RMSE) and Peak Signal-to-Noise Ratio (PSNR) of the reconstructed images.

Results and Discussions

The proposed method is tested on human head data obtained using 1.5T GE scanner (St. Mary’s Hospital, London), with eight channel head coil, originally acquired in a Cartesian fashion using Fast Spin Echo pulse sequence. The data acquisition parameters are: FOV =20cm, TR=500ms, TE=10ms, bandwidth=31.25 kHz, slice thickness=3mm and flip angle = 500. The acquired fully sampled Cartesian data is transformed into fully sampled radial data using Fessler Toolbox ⁸. The number of fully sampled radial projections are calculated using the relation: $$$(π/2) × FOV$$$ ^2. Finally, this fully sampled radial data is under-sampled at AF=4, 6 and 9.

The simulation results are shown in Figure 2: column A shows the reconstruction results of the proposed scheme whereas results of conventional pseudo Cartesian GRAPPA have been shown in column B. As can be verified from Figure 2, the proposed method reconstructs the solution image efficiently at AF=4, whereas conventionally used pseudo-Cartesian GRAPPA scheme shows some artifacts. Furthermore, the proposed method provides better reconstruction results even at higher AF (i.e. at 6 and 9) as shown in Figure 2.

A comparison of the proposed scheme and pseudo-Cartesian GRAPPA in terms of quantifying parameters (AP, RMSE and PSNR) is given in Table 1. The results show that the proposed method provides up to 87% improvement in AP, 54% improvement in RMSE and 12% improvement in terms of PSNR at AF=4 in the reconstruction results as compared to pseudo-Cartesian GRAPPA.

Conclusion

Acknowledgements

References

1. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42(5):952-962.

2. Wright KL, Hamilton JI, Griswold MA, Gulani V, Seiberlich N. Non-Cartesian parallel imaging reconstruction. J Magn Reson Imaging. 2014;40(5):1022-1040.

3. Seiberlich N, Breuer F, Heidemann R, Blaimer M, Griswold M, Jakob P. Reconstruction of undersampled non-Cartesian data sets using pseudo-Cartesian GRAPPA in conjunction with GROG. Magn Reson Med. 2008;59(5):1127-1137.

4. Seiberlich N, Breuer F, Blaimer M, Jakob P, Griswold M. Self-calibrating GRAPPA operator gridding for radial and spiral trajectories. Magn Reson Med. 2008;59(4):930-935.

5. Otazo R, Kim D, Axel L, Sodickson DK. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn Reson Med. 2010;64(3):767-776.

6. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-1195.

7. Irfan AS, Nisar A, Shahzad H, Omer H. Sensitivity Maps Estimation Using Eigenvalues in Sense Reconstruction. Appl Magn Reson. 2016;47(5):487-498.

8. Fessler JA, Sutton BP. Nonuniform fast fourier transforms using min-max interpolation. IEEE Trans Signal Process. 2003;51(2):560-574.