2438
Rapid Abdominal Imaging Using Highly Accelerated Projection Imaging (HAPI1Department of Neurosurgery, Medical College of Wisconsin, Milwaukee, WI, United States, 2Center for Imaging Research, Medical College of Wisconsin, Milwaukee, WI, United States, 3Department of Radiation Oncology, Medical College of Wisconsin, Milwaukee, WI, United States, 4Department of Radiology, Medical College of Wisconsin, Milwaukee, WI, United States
Synopsis
Our group recently reported a new fast radial imaging method called Highly Accelerated Projection Imaging (HAPI) with coil sensitivity encoding. We demonstrated that radial projections acquired at specific angles and at high resolution resulted in a well-conditioned matrix equation. In the previous work, the performance of HAPI was demonstrated with simulations and a simple phantom scan using an 8-channel receive array. In the study presented here, the HAPI method was tested in vivo with volunteers.
Introduction:
Rapid MRI techniques require sampling the k-space as fast as possible. For further acceleration, only a portion of the k-space is sampled and missing data is synthesized using parallel imaging techniques. We recently reported a new fast radial imaging method called Highly Accelerated Projection Imaging (HAPI)1 that is capable of reconstructing an image from a small number of radial projections. Radial projections acquired at specific angles and at high resolution resulted in a well-conditioned matrix equation. In the previous work, the performance of HAPI was demonstrated with simulations and a phantom scan. Here we present in vivo abdominal imaging results and compare with other conventional reconstruction methods.
Methods:
Given high resolution radial k-space data, the 1D inverse Fourier transform of each spoke yields a projection of the imaged object. The isofrequency paths formed by the frequency encoding gradients are referred to as rays. The measured projections for each RF coil can be modeled as the integral along each ray of the object (x) times the coil sensitivity profiles (C) and times the fraction of the ray (F) covering each reconstructed voxel. The object can therefore be inversely solved for by solving the following equation.
x = argminx ||FCx - p||22 + λ || Tx ||1
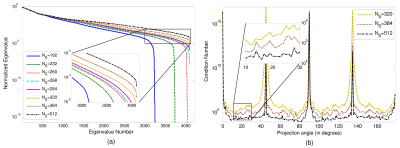
The quality of the solution is dependent on the condition of the encoding matrix A = FC. This condition depends on the acquired projection angles and the ratio of the acquired resolution to the reconstructed resolution, as we published earlier1. Fig.1. shows the effects of projection angles and number of samples for each projection on the condition of the matrix. In this study, the HAPI reconstruction incorporated 2D total variation (TV) regularization. The problem was solved via conjugate gradient (CG) methods.
The study was approved by the IRB and written consent was obtained. Stack-of-stars spoiled gradient echo data were acquired on a 1.5T MR-Linac (Unity, Elekta Instruments) with an 8-channel receive coil. The data were acquired at a base resolution of 512x512 with an in-plane FOV of 340 mm. For a central slice, five reconstructions from 16 spokes were performed at a reconstructed resolution of 128x128: non-uniform FFT (NUFFT)2, CG-SENSE3, CG-SENSE with TV regularization4, HAPI, and HAPI with TV regularization. In the non-HAPI cases, the images were reconstructed at 512x512 and resampled to 128x128. For HAPI reconstruction, the optimal projection angles of {7 14 18 22 28 32 36 56 60 64 68 72 80 110 116 129} degrees were chosen based on the trends seen in Fig.1.
Results:
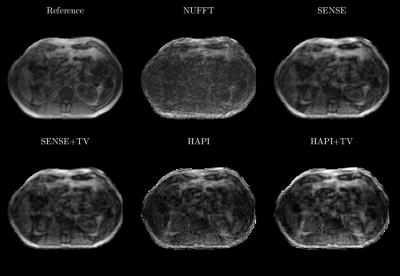
The results are shown in Fig.2. A reference image reconstructed from 512 spokes is shown in the top left. The NUFFT reconstruction is highly corrupted by streaking artifacts as expected given that only 16 spokes were used. The CG-SENSE algorithm was able to largely remove the streaking artifacts. Artifacts are further removed when SENSE was used in conjunction with TV regularization. The HAPI image also greatly improves image quality relative to the NUFFT image. It is sharper than the CG-SENSE reconstruction, but also contains residual streaking artifacts. The HAPI+TV reconstruction helped remove the streaking and noise from the images at the expense of smoother edges in the images.Discussion:
The in vivo HAPI images were able to suppress the undersampling artifacts compared to the NUFFT reconstruction. The HAPI algorithm performs similarly well as traditional sensitivity encoding with non-Cartesian trajectories. An advantage of HAPI compared with CG-SENSE is reconstruction speed. Since HAPI operates in the projection domain, no time-consuming fast Fourier transforms are required to perform data consistency checks. The HAPI reconstructions ran in approximately 1 second while the CG-SENSE reconstructions took approximately 2 seconds. In a follow-up study, a robust comparison between the computational complexities of these two methods will be performed.Conclusion:
In This study, the highly accelerated projection imaging (HAPI) algorithm was used to reconstruct in vivo images for the first time. While some further optimizations need to be performed in terms of the number and angle of acquired k-space spokes, the images it produces are comparable to those obtained via CG-SENSE. However, the superior reconstruction speed could be advantageous in real-time dynamic imaging applications. The best set of projection angles need to be explored for HAPI for a given set of RF coils using a systematic search rather than a heuristic approach used here. Genetic Search algorithms could be able to provide a better set of projection angles for HAPI. This way, HAPI might be able to reconstruct high fidelity images with fewer spokes as we have shown earlier with simulations1.Acknowledgements
No acknowledgement found.References
[1] Ersoz A, Arpinar VE, Muftuler LT. Highly accelerated projection imaging with coil sensitivity encoding for rapid MRI. Med Phys 2013;40:022305. doi:10.1118/1.4789488.
[2] Fessler JA, Sutton BP. Nonuniform fast fourier transforms using min-max interpolation. IEEE Trans Signal Process 2003;51:560–74. doi:10.1109/TSP.2002.807005.
[3] Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med 2001;46:638–51. doi:10.1002/mrm.1241.
[4] Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn Reson Med 2007;57:1086–98. doi:10.1002/mrm.21236.
Figures