2137
High-Resolution Dynamic Myocardial T1 Mapping Using Low Rank Tensor Regularization MethodsBurhaneddin Yaman1,2, Sebastian Weingärtner1,2,3, Steen Moeller2, Nikolaos Kargas1, Nicholas Sidiropoulos4, and Mehmet Akçakaya1,2
1Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 3Computer Assisted Clinical Medicine, University Medical Center, Heidelberg University, Mannheim, Germany, 4University of Virginia, Charlottesville, VA, United States
Synopsis
Recently a new method called TOPAZ was developed for cardiac phase-resolved myocardial T1 mapping, which is performed in breath-hold duration that subsequently limits its spatial resolution. These datasets are multidimensional which makes tensor regularization a natural fit for regularization. In this work, we sought to compare different tensor regularization techniques to enable high-resolution TOPAZ acquisitions.
INTRODUCTION
Myocardial T1 mapping is typically performed using single-shot imaging with 150-200 ms temporal resolution. However, for subjects with high heart rates, improved temporal resolution may be needed, especially for quantifying mobile structures, like papillary muscles. Recently a new technique, called TOPAZ [1], which is performed in a breath-hold, was proposed to acquire T1 maps in a cardiac phase-resolved manner at improved temporal resolutions. However, spatial resolution of TOPAZ is limited due to breath-hold durations. Thus, regularization may be desirable for high-resolution imaging in order to alleviate the noise amplification. TOPAZ acquisitions are multi-dimensional consisting of two spatial, a cardiac phase and a contrast dimension. Low-rank matrix regularization has been studied in this context [2]. However, low-rank tensor regularization (LRTR) [3] may be a better fit to mitigate the noise amplification for such datasets since low-rank matrix regularization is limited to pairwise interactions, which hinders capturing interaction between multiple dimensions. In this work, we sought to compare different LRTR techniques based on PARAFAC [4] and Tucker [5,6] decompositions for high-resolution TOPAZ acquisitions.METHODS
Imaging was performed on five healthy subjects at 3T, using a 30-channel receiver coil array with resolution=1.3×1.3mm2, FOV=300×225 mm2, temporal resolution=60ms, partial Fourier=6/8, in-plane acceleration=3 and ACS lines=24. Datasets used in this study $$$ X (x,y,t,c) \in {\mathbb C}^{M\times N \times T \times C} $$$ were 4-dimensional where $$$(x,y)$$$ were the spatial dimensions, $$$t$$$ was the cardiac phase and $$$c$$$ represented different T1 contrasts. This led to $$$T$$$ cardiac phases and $$$C$$$ different T1-weightings per phase for a total of $$$T*C$$$ images in each dataset. Subsampled k-space data were first reconstructed using GRAPPA [7] and combined using SENSE-1 coil combination. Different tensor decompositions (Fig.1) were applied to these image series to reduce noise amplification arising from GRAPPA. PARAFAC decomposition represents a tensor as a sum of rank one tensors, while Tucker decomposition factorizes a tensor into a core tensor multiplied with factor matrices along each mode. For both techniques, global processing was applied by processing the whole dataset, which contains all tissue types and contrasts, and local processing was performed by processing smaller patches in x-y plane, which is likely to have similar tissue properties. The patches were of size $$$8\times 8 \times T \times C$$$, and the processed patches were combined via averaging. Rank for PARAFAC decomposition was selected empirically [4]. Since Tucker decomposition has multilinear rank, the high degrees of freedom hinders empirical rank selection. Thus, we proposed a rank selection approach for Tucker method using a principal component analysis based approach, which applies proportion of variance (PoV) to each factor matrix in the tensor. In PoV approach, eigenvalues with negligible contribution to variance and the largest eigenvalue value [8] are discarded and a proportion of the eigenvalues is used to choose the rank for the factor matrix. Hence, multilinear Tucker decomposition was formed using the ranks of factor matrices. For each method, the T1 values and spatial variability are measured as the mean and standard deviation myocardial T1 for each cardiac phase. These are reported as averages across all cardiac phases.RESULTS
Representative quantitative TOPAZ T1 maps are shown in Fig. 2. For both tensor decompositions, local LRTR substantially alleviated the noise artifacts compared to global LRTR and GRAPPA, although some residual blurring is apparent in the local Tucker LRTR approach. Across all subjects, for both tensor decomposition approaches, the absolute differences in estimated mean T1 values were <1.5% compared to parallel imaging for all subjects. The spatial variability of myocardial T1 times across all subjects were 352±33ms for GRAPPA, 213±23ms for global PARAFAC and 138±22ms for local PARAFAC, 190±27ms for global Tucker and 149±22ms for local Tucker methods. For both tensor decompositions, local LRTR substantially alleviated the noise artifacts compared to global LRTR. Fig. 3 depicts the T1 times through cardiac phases across a cross-section of the heart. Both local LRTR methods significantly eliminate noise artifacts present in GRAPPA, while not hindering identification of tissue borders.DISCUSSION
In this study, LRTR was applied to an image series from TOPAZ T1 mapping acquisition in order to mitigate noise amplification. Local processing of small patches in both PARAFAC and Tucker decompositions outperforms global processing of the whole volume data. Additionally, local LRTR has a computational advantage over global LRTR since each patch can be processed independently on GPU or multi-cores.CONCLUSION
Local low-rank tensor regularization techniques improve the spatial resolution of TOPAZ T1 mapping to 1.3 mm in-plane resolution despite scan-time limitations imposed by the breath-hold duration.
Acknowledgements
Grant support: NIH R00HL111410, NIH P41EB015894, NSF CCF-1651825 and NSF IIS-1704074References
[1] Weingärtner, MRM, 2018; [2] Zhang, MRM, 2015; [3] Trzasko, ISMRM 2015; [4] Yaman, IEEE CAMSAP, 2017; [5] He, IEEE Trans Med Imaging, 2016; [6] Christodoulou, Nat Biomed Eng, 2018 [7] Griswold, MRM, 2002; [8] Baik, Ann. Probab, 2005.Figures
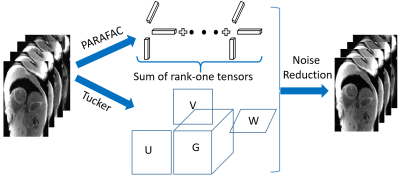
Figure
1. PARAFAC and Tucker decompositions
were used for tensor regularization. PARAFAC decomposes the tensor into sum of
rank one tensor; Tucker method is a form of high order singular value
decomposition that decomposes the tensor into a core tensor multiplied with
factor matrices along each mode.
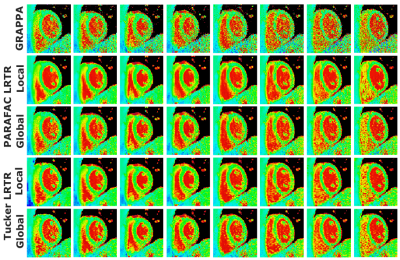
Figure 2.
Dynamic quantitative T1 mapping of 8 representative cardiac phases
out of all 16. Major noise variation can be seen in GRAPPA images arising from
linear parallel imaging reconstruction. Global PARAFAC and Tucker LRTR methods
reduce the noise amplification in GRAPPA images. Local PARAFAC and Tucker LRTR
techniques further suppress the residual noise artifacts and noise
inhomogeneity present in global LRTR methods. Spatial variability across
cardiac phases for this subject was 304±44 for GRAPPA, 170±20 ms for global
PARAFAC, 120±23
ms for local PARAFAC, 163±15 ms for global Tucker and 125±21 ms for local Tucker
decompositions.
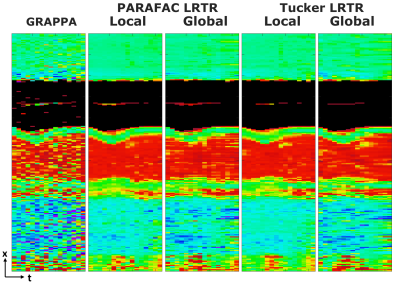
Figure 3. T1
times through cardiac phases across a cross section of the heart. GRAPPA
suffers from major noise variations which hinder characterization of tissue
borders. Both PARAFAC and Tucker regularization techniques mitigate the noise
substantially, enabling clear assessment of tissue boundaries.