Synopsis

A method for whole-brain shim coil design for Ultra-High field is proposed using Singular Value Decomposition of tailored stream functions to create a small set of independently driven coils providing the same performance as shim inserts with numerous high-order spherical harmonics coils.

Introduction

High-order Spherical Harmonics (SH) shim inserts¹ and multi-coil arrays^2,3 (MCA) are popular approaches to reduce magnetic field inhomogeneity in the human at Ultra-High Field (UHF). However, their conception has neglected to capture inter-subject field similarities, which could be used to reduce the amount of coils needed to reach a given level of homogeneity.

Here we revisit the Singular Value Decomposition of 3D human brain fieldmaps⁴ by applying SVD over more tractable 2D stream functions (SF) tailored for each fieldmap over a cylindrical surface with our original computational method⁵. A reduced set of SF-SVD coils is extracted to compose a whole brain shimming system at UHF. For the sake of demonstration, the hereby study is limited to three independently-driven cylindrical coils, but could easily be extended to more channels.

Methods

We first built a database of 55 three-dimensional ΔB₀ brain maps from informed and consenting adults. These maps were acquired at a 3T Siemens Magnetom-Prisma imager with 1.7-mm isotropic resolution and rescaled to 7T, since a shim system for UHF is intended. FSL’s brain extraction tool was used to exclude non-brain voxels and, as a baseline, a re-shim at 2^nd order SH was performed in the brain mask. A sample of 25 maps (design set) was randomly picked and their residual fields used as target for tailored stream function computation and shim coil generation.

Defining three different cylindrical coil formers of 300-mm length and of 138-mm, 144-mm, and 150-mm concentric radii at the gradients isocenter, a set of 25 tailored shim coils are generated for each former. Each coil is designed to reduce as much as possible the inhomogeneity of the map used as target field, while keeping acceptable levels of power consumption (< 40 W)⁵. Field inhomogeneity is defined as the field standard deviation in each brain.

The three resulting sets of 25 stream functions are independently post-processed using Singular Value Decomposition. A new set of virtual SF-SVD coils is thus obtained at each cylindrical radius (Figure 1).

As higher singular values address the most common brain features, the stream functions of a given high SF-SVD rank are assumed to be similar when going from one radius to the next. Thus, for the 138-mm coil, only the stream function of highest singular value is kept; for the 144-mm radius coil, the second highest; and for the 150-mm radius coil, the third highest (Figure 2).

To guarantee field fidelity when discretizing current surface densities into wires⁶, and help reduce electric current, the amount of wires is maximized for a 20-AWG wire gauge and 5 wire layers per coil.

The magnetic field generated by each of the three SF-SVD coils is evaluated in the volume encompassing all brains; then for each fieldmap, three shim currents are computed from a Least Squares fitting algorithm. This was performed on the 25 brains of the design set and on the 30 remaining maps (test set).

For comparison, the performance of a SH-shim insert going up to 5^th-order was assessed without power limitation.

All simulations were performed in MATLAB®.

Results

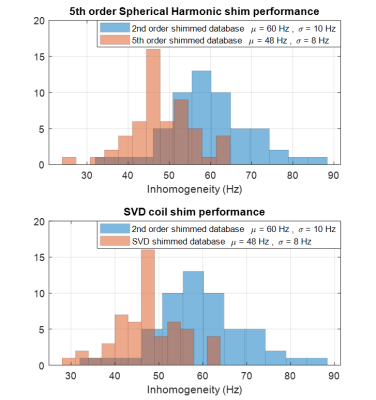
Average global inhomogeneity of the 2^nd-order shimmed database was 60±10Hz, regardless of the sample set.

Applying 5^th-order SH shim over each set, 48±8Hz average inhomogeneity was achieved for all sets, bringing its reduction to 20% (Figure 3a).

SF-SVD coil shimming over the entire database(Figure 3b), design and test sets resulted in average inhomogeneity of 48±8Hz, 47±8Hz and 49±8Hz respectively (reduction was 20%, 21% and 18%). Average currents per coil were 2.3A, 1.3A and 1.2A for first, second and third SF-SVD coils respectively.

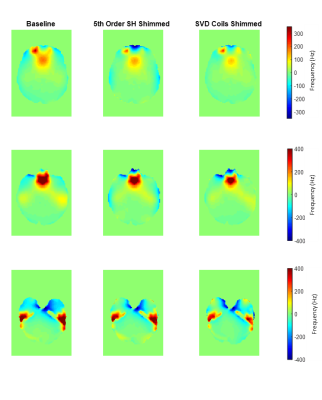
Figure 4 shows axial B0 brain slices of a random subject after shimming with either one of the discussed coil inserts.

Discussion and conclusion

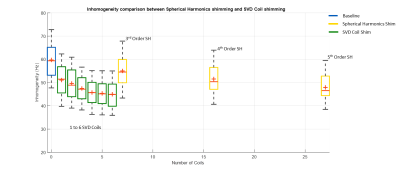
The three-channel SF-SVD-coil insert provides shimming performance equivalent to that of a complete 5^th-order shim insert with 27 coils and unlimited power. Its performance over the test set was only 3% worse than over the design set, which shows it was still effective over new brains, but also that more maps might be necessary in the design set.

Provided space is available for a thicker shim insert, more SF-SVD coils could be added at larger radii to increase performance, but preliminary simulations show that beyond 4 coils, the overall improvement is small (Figure 5).

Given an anatomical target such as the human brain, the SF-SVD coil design seems to be a great alternative to traditional SH coil or current MCA systems as they considerably reduce the space and cost required to reach a certain level of field homogeneity.

Acknowledgements

References

1. J.W. Pan, K. Lo, H.P. Hetherington. Role of very high order and degree B0 shimming for spectroscopy imaging of the human brain at 7 Tesla. Magn Reson Med, 2012 Oct; 68(4): 1007-1017.

2. C. Juchem, et al. Dynamic multi-coil shimming of the human brain at 7 T. Journal of Magnetic Resonance, 2011 Oct; 212(2):280-8.

3. J. Stockman, L.L. Wald. In vivo B0 field shimming methods for 7 T. Neuroimage, 2018 Mar; 168:71-87.

4. E. Adalsteinsson, S.M. Conolly, et al. Design of Dedicated Shim Fields. International Society of Magnetic Resonance in Medicine, 1999; 447.

5. B.P. Meneses, A. Amadon. The Dipole Boundary Method : a simple approach to compute stream functions for shim coil design. ISMRM 2019

6. G.N. Peeren. Stream function approach for determining optimal surface currents. Journal of Computational Physics, 2003 Oct; 191(1):305-321