1257
Efficient Intravoxel B0 Inhomogeneity Corrected Reconstruction of Multi-Gradient-Echo Images Using A Low-Rank Encoding Operator1Department of Bioengineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 2Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States
Synopsis
Intravoxel macroscopic B0 field inhomogeneity is common source for image artifacts, and can cause significant errors in quantitative analysis of the imaging data, particularly for gradient-echo-based acquisitions. This work presents a new method for intravoxel B0 inhomogeneity corrected reconstruction. Specifically, we derived a signal model that incorporates intravoxel B0 variations, and introduced a low-rank approximation to the encoding operator. This approximation allows for very efficient computation of the forward model, which can be integrated into any regularized reconstruction formulation. Effective correction for multi-gradient-echo data were demonstrated. We expect the proposed method to be useful for a range of applications involving T2* contrast.
INTRODUCTION
Macroscopic B0 field inhomogeneity induced intravoxel dephasing can cause significant artifacts in MR images and errors in subsequent quantitative analysis, especially for acquisitions involving multiple gradient echoes1,2. Decreasing voxel size can mitigate this problem, but at the expense of longer acquisitions. One main approach to address this issue is to apply post-reconstruction correction by deriving intravoxel B0-induced modulation functions2,3,4. However, this voxel-wise modulation function is reconstruction dependent and can be rather difficult to derive for advanced reconstruction methods4. An alternative approach is to perform B0-corrected reconstruction5,6, which can be very computationally expensive because of the need to include intravoxel field variations into the signal model6. In this work, we develop a new method for efficient B0-corrected reconstruction. Specifically, we derived a signal model that incorporates intravoxel field variations, and introduced a low-rank approximation to the encoding operator under piecewise linear inhomogeneity assumption, allowing very efficient computation of the forward model. The proposed method can be incorporated into general regularized reconstruction formulations. Results from multi-echo GRE data demonstrated effective correction of macroscopic B0 effects. We expect the proposed method to be useful for various imaging applications involving $$$T_2^*$$$contrast, including fMRI, diffusion imaging, multi-echo GRE imaging and MR spectroscopic imaging.THEORY AND METHODS
A general signal equation for multi-gradient-echo acquisition can be written as follows (ignoring the phase effects during each short readout period)
$$d_c(\mathbf{k},t)=\int_{-\infty}^{\infty}s_c(\mathbf{r})\rho(\mathbf{r},t)e^{i2\pi\Delta f(\mathbf{r})t}e^{-i2\pi\mathbf{kr}}d\mathbf{r} \qquad\qquad\quad\quad [1]$$
where $$$\rho(\mathbf{r},t)$$$ is the multi-echo images with $$$t$$$ the echo times, $$$\Delta f(\mathbf{r})$$$ the B0 inhomogeneity, $$$s_c(\mathbf{r})$$$ the coil sensitivity, $$$\mathbf{r}$$$ and $$$\mathbf{k}$$$ vectors denoting the spatial and k-space coordinates. Discretizing Eq. [1] using rectangular voxel basis functions, we can obtain4
$$d_c(\mathbf{k}_m,t)=\sum_ns_{c,n}\boldsymbol{\rho}_n(t)e^{-i2\pi\mathbf{k}_m\mathbf{r}_n}\mathbf{W}_{mn}(t) \qquad\qquad\qquad\quad [2]$$
where $$$\{s_{c,n}\}$$$ and $$$\{\boldsymbol{\rho}_n(t)\}$$$ represent the sensitivity maps and the unknown images, respectively. The $$$M\times N$$$ matrix $$$\mathbf{W}(t)$$$ encodes the effects of B0 inhomogeneity (echo dependent). $$$M$$$ is the total number of k-space samples each echo and $$$N$$$ is the number of voxels. With a locally linear assumption on $$$\Delta f(\mathbf{r})$$$, $$$\mathbf{W}(t)$$$ can be simplified to $$$\mathbf{W}_{mn}(t)=e^{i2\pi f_nt}\text{sinc}[(\mathbf{k}_m-\mathbf{g}_nt)\Delta\mathbf{r}]$$$ with $$$\mathbf{g}_n$$$ being 3x1 vectors capturing the within-voxel field gradients along all three spatial directions.
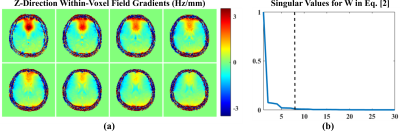
It can be seen that 1) storing the matrix $$$\mathbf{W}$$$ can be memory prohibitive and 2) directly evaluating Eq. [2] is rather computationally intenstive, especially for high-resolution 3D reconstruction, because the coupling between $$$\mathbf{W}$$$ and $$$e^{-i2\pi\mathbf{k}_m\mathbf{r}_n}$$$ prevents direct application of FFT. However, we recognize that $$$\mathbf{W}$$$ can be accurately approximated by a low-rank factorization (illustrated in Fig. 1), i.e., $$$\mathbf{W}(t)\approx\sum_{l=1}^L\mathbf{u}_{l}(t)\mathbf{v}_{l}^T(t)$$$ where $$$\mathbf{u}$$$, $$$\mathbf{v}$$$ are column vectors and $$$L\ll M,N$$$. Accordingly, Eq. [2] can be rewritten in the following matrix-vector multiplication form
$$\mathbf{d}_{c,t}=\sum_{l=1}^L\mathbf{u}_l(t)\odot\{\mathbf{F}_{\Omega}(\mathbf{v}_l(t)\odot\mathbf{S}_c\boldsymbol{\rho}_{t})\}=\mathbf{E}_{c,t}\boldsymbol{\rho}_{t} \qquad\qquad\quad [3]$$
with $$$\mathbf{d}_{t}$$$ containing data for the echo image $$$\boldsymbol{\rho}_{t}$$$, $$$\mathbf{F}_{\Omega}$$$ denoting the Fourier transform operator with sampling mask $$$\Omega$$$, $$$\odot$$$ the point-wise multiplication and $$$\mathbf{S}_c$$$ the sensitivity modulation. This low-rank decomposed encoding operator in Eq. [3] can be readily incorporated into any reconstruction formulation and calculated efficiently (with L FFTs). Therefore, the final intravoxel B0 inhomogeneity corrected multi-echo images are jointly reconstructed by solving the following regularized least-squares problem
$$\{\hat{\boldsymbol{\rho}}_{t}\}=\arg\underset{\{\boldsymbol{\rho}_{t}\}}{\min}\sum_{t}\sum_{c}\left\Vert\mathbf{d}_{c,t}-\mathbf{E}_{c,t}\boldsymbol{\rho}_{t}\right\Vert_2^2+\lambda R(\{\boldsymbol{\rho}_{t}\}),$$
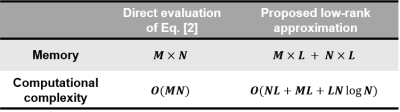
for which different fast algorithms can be used for different choices of $$$R(\cdot)$$$. Note that for each t, the factorization $$$\{\mathbf{u}_l\}$$$ and $$$\{\mathbf{v}_l\}$$$ can be computed using only sparse samples in $$$\mathbf{W}$$$ (due to low-rankness), thus avoiding explicitly storing the huge $$$\mathbf{W}$$$ in memory, making efficient implementations possible7,8. Table 1 further highlights the memory and computational complexity reduction offered by the proposed method.
RESULTS
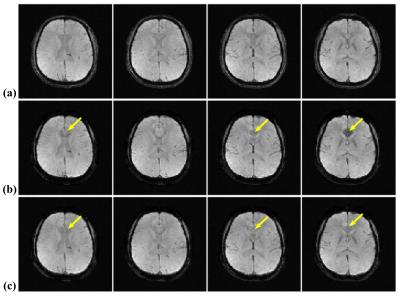
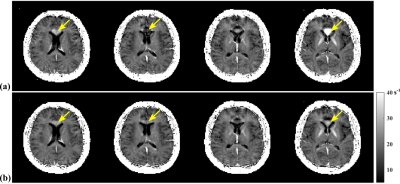
In vivo experiments were performed to evaluate the proposed method. First, a high-resolution (HR) multi-echo 3D GRE data (0.9x0.9x1.5mm3) was acquired on a 3T Siemens scanner using a 20-channel head coil. Lower-resolution (LR) data was generated by a k-space truncation (to a 2x2x3mm3 voxel size). Figure 2 compares a reconstruction from the HR data (phase removed at the original resolution followed by truncating the k-space data), a Fourier reconstruction from the LR data, and the proposed reconstruction from the LR data with $$$L=8$$$. As can be seen, the HR data has minimal intravoxel dephasing due to the small voxel size, while the LR Fourier reconstruction has apparent artifacts in regions with strong susceptibility variations. The proposed method significantly reduced these artifacts (Fig. 2c), producing similar images as the truncated magnitude HR data. The R2* maps shown in Fig. 3 further demonstrate the utility of the proposed method in improving the accuracy of quantitative analysis for multi-gradient-echo data.
CONCLUSION
A new macroscopic B0 inhomogeneity corrected reconstruction method has been developed. The proposed method can work synergistically with any regularized reconstruction formulation, and enable very efficient during-reconstruction correction of intravoxel inhomogeneity induced artifacts.Acknowledgements
No acknowledgement found.References
1. Ordidge et al., Assessment of relative brain iron concentrations using T2‐weighted and T2*‐weighted MRI at 3 Tesla. Magn. Reson. Med., 1994;32:335-341.
2. Fernandez‐Seara and Wehrli, Postprocessing technique to correct for background gradients in image‐based R2* measurements. Magn. Reson. Med., 2000;44:358-366.
3. Hernando et al., R2* mapping in the presence of macroscopic B0 field variations. Magn. Reson. Med., 2012;68:830-840.
4. Yablonskiy et al., Voxel spread function method for correction of magnetic field inhomogeneity effects in quantitative gradient-echo-based MRI. Magn. Reson. Med., 2013;70:1283-1292.
5. Sutton et al., Fast, iterative image reconstruction for MRI in the presence of field inhomogeneities. IEEE Trans. Med. Imaging, 2003;22:178-188.
6. Ngo and Sutton, R2* mapping for robust brain function detection in the presence of magnetic field inhomogeneity. IEEE-EMBC, 2014.
7. Liang, Spatiotemporal imaging with partially separable functions. IEEE-ISBI, 2007.
8. Haldar and Hernando, Rank-constrained solutions to linear matrix equations using power factorization, IEEE Signal Process. Lett., 2009;16:584-587.
Figures